美しすぎる遠回り！INDEXとSEQUENCEで「3乗」を求める関数パズル
「Excelで、セルの行番号を3乗する数式？…そんなの=ROW()^3で一発じゃないか。」
そう思ったあなた、もちろん大正解！
実務でこの課題に直面したら、それが100点満点の回答です。
でも、ここは「Excelで暇つぶし」をするブログ。
最短距離で正解にたどり着くだけでは、面白くないですよね？
今回は、あえて壮大な回り道をして、同じゴールを目指してみようと思います。
ご紹介するのは、こちらの数式です。
=INDEX(SEQUENCE(ROW(),ROW(),ROW(),ROW()),ROW(),ROW())
「なんだこれは…！？ ROW関数が6回も出てくるじゃないか！なぜこんな複雑なことを？」
う思いますよね？
この一見、非効率で冗長に見える数式にこそ、関数の組み合わせが織りなす、ある種の「美しさ」が隠されているのです。
今回のテーマは、「答え」ではなく、そこにたどり着くまでの「道のり」を楽しむ、純粋な関数パズルです。
この数式の謎を解き明かすプロセスを通じて、Excelへの理解が、さらに深まること間違いなしです。
今回のミッション
ゴール
Excelのワークシート関数を使い、セルの行番号の3乗（例: A5セルなら125）を計算する。
挑戦者：4つの数式
今回のパズルには、4つの数式が登場します。
- 正攻法①:
=POWER(ROW(),3) - 正攻法②:
=ROW()^3 - 正攻法③:
=PRODUCT(ROW(),ROW(),ROW()) - 今回の主役:
=INDEX(SEQUENCE(ROW(),ROW(),ROW(),ROW()),ROW(),ROW())
方法1, 2, 3：正攻法で一瞬！POWER, ^, PRODUCT
まずは、実務で使うべき、正しくて効率的な方法から見ていきましょう。
=POWER(ROW(),3): POWER関数はべき乗を計算する関数です。ROW()を3乗する、最も分かりやすい数式ですね。=ROW()^3: ご存知、ハット記号^を使ったべき乗の計算です。これも一般的です。=PRODUCT(ROW(),ROW(),ROW()): PRODUCT関数は引数の積を返します。ROW()を3回掛けることで、3乗を実現しています。
「こんなに簡単で分かりやすい方法があるのに、なぜわざわざあの複雑な数式を…？」
その答えを探しに、いよいよ本日のメインディッシュ、美しき遠回りの旅に出かけましょう！
方法4：美しき遠回り！INDEX(SEQUENCE(…))の謎を解く
考えかた
この数式の考え方は、非常にユニークです。
まずSEQUENCE関数で行番号nを使って、n行n列の正方形の盤面を作り出します。
そして、その盤面の右下隅にある最後のマスの値をINDEX関数で取り出すと、それがなぜか、寸分違わずnの3乗になっている…という、まるで奇術のようなロジックです。
数式と解説
=INDEX(SEQUENCE(ROW(),ROW(),ROW(),ROW()),ROW(),ROW())
それでは、A5セル（ROW()が5を返す）を例に、この数式の動きをステップ・バイ・ステップで見ていきましょう。
STEP1: SEQUENCE関数が「魔法の盤面」を作る
まず、内側のSEQUENCE関数が評価されます。
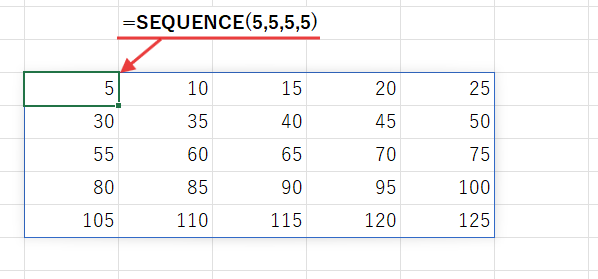
A5セルではROW()が5なので、SEQUENCE(5,5,5,5)となります。
これは、「5行5列で、開始値が5、増分も5の連続データの配列を作れ」という命令です。
その結果、Excelのメモリ上には、以下のような盤面が生成されます。
STEP2: INDEX関数が「右下の宝物」を抜き出す
次に、外側のINDEX関数が、この盤面を処理します。
数式は、=INDEX( [STEP1の盤面] , 5, 5) となります。
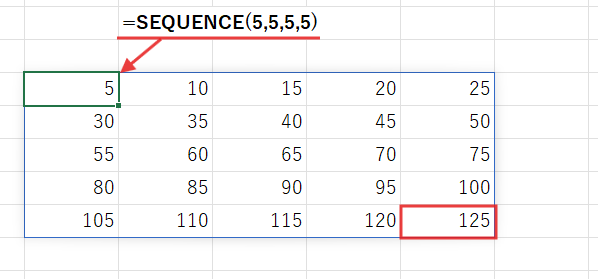
これは、「盤面の5行目、5列目にある値を抜き出せ」という命令です。
盤面の右下隅にある、最後の宝物…そう、125です！
そして、125は、見事に5の3乗になっていますね！
なぜ、必ず「3乗」になるのか？数学的な証明
「たまたま5だから上手くいっただけじゃないの？」
いいえ、これはどんな行番号nでも必ず成立する、美しい数学的法則なのです。
n行n列の盤面の、n行n列目（一番最後）のマスに書かれる数値を求めてみましょう。
等差数列の一般項を求める公式 初項 + (項数 – 1) 公差 を使います。
- 初項: n (ROW())
- 公差: n (ROW())
- 項数: 盤面の一番最後のマスは n×n 番目なので、項数は n² です。
これを公式に当てはめると…
n + (n² - 1) * n
= n + n³ - n
= n³
ほら！ちゃんとnの3乗になりました！
この数式は、見た目の複雑さとは裏腹に、極めて明快な数学的法則に基づいていたのです。
まとめ：目的は「答え」か、それとも「道のり」か
お疲れ様でした！
今回は、行番号の3乗を計算するというシンプルなゴールに対して、正攻法とは全く違う、壮大な回り道をする関数パズルに挑戦しました。
私たちは、=ROW()^3という簡単な答えを、最初から知っていました。
しかし、あえて複雑な=INDEX(SEQUENCE(…))という数式の謎を解き明かす旅に出ました。
この暇つぶしの本当の価値は、125という「答え」を見つけることではありません。
その答えに至るまでの、一見無駄に見える「道のり」の中で、関数の組み合わせが織りなす予期せぬ法則性や、その背後にある数学的な美しさに気づくこと。それこそが、最大の醍醐味なのです。
あなたのExcelライフが、また一つ、楽しいものになったなら幸いです！
