はじめに:その格子模様、関数だけで作れますか?
Excelのセルを「■」と「□」で塗り分けて、美しい格子模様(市松模様)を作りたい!

「ふふん、そんなの『条件付き書式』で、=MOD(ROW()+COLUMN(),2)=0 を使えば一発だよ!」
そう思ったあなた、大正解!
それが最も簡単でスマートな方法です。
でも、ちょっと待ってください!
もし、その「条件付き書式」が、今日から使用禁止になったとしたら?
「え、機能を使わずに、どうやって模様を…?」
そう、今回のテーマは、一つの数式をA1セルに入力するだけで、A1:D4の範囲に「■」と「□」の格子模様をスピルさせて描き出す、という純粋な関数パズルです!
基本形は =IF(条件式, "■", "□") です。
この「条件式」の部分を、今回は4つの異なるアプローチで考え、関数の多様性を探求していきます。
今回はここ最近のテーマの中でかなりシンプルな部類です。
Excel初心者の方も、配列計算の「入口」として、ぜひ楽しんでいってくださいね!
Excelの基本機能などやVBAで格子模様を作成する方法は以下の記事で紹介しています。
本記事では、無料のWeb版Excelを使用して検証および画像の作成を行っています。Windowsはもちろん、MacやLinuxの方もブラウザさえあれば挑戦できます!
準備:ゴールを確認する
何事も、まずは準備から。まっさらなシートを用意してください。
ゴールは、A1セルに一つの数式を入力するだけで、A1:D4の範囲に、以下のような格子模様がスピルして表示されることです。

さあ、このシンプルなゴールに向かって、4つの異なる道を冒険しましょう!
4つのアプローチで、「格子模様」を攻略せよ!
関数の詳細な仕様については、Microsoft公式のヘルプも参考にしてください。
アプローチ1:ROW + COLUMN + ISEVEN(王道)
考えかた
格子模様を作る上で、最も有名で、最も直感的なロジックです。
各セルの「行番号」と「列番号」を足し算し、その結果が「偶数」か「奇数」かで、「■」と「□」を塗り分けます。
数式と解説
=IF(ISEVEN(ROW(A1:D4)+COLUMN(A1:D4)),"■","□")
この数式、内側から順に見ていきましょう。
1. ROW(A1:D4): まず、ROW関数が、指定された範囲(A1:D4)の「行番号」を配列として返します。結果は {1;2;3;4} という、縦一列の配列になります。
2. COLUMN(A1:D4): 次に、COLUMN関数が、指定された範囲(A1:D4)の「列番号」を配列として返します。結果は {1,2,3,4} という、横一列の配列になります。

3. ... + ...: ここが最大のポイント!まず、Excelの「ブロードキャスト」機能により、縦配列 {1;2;3;4} と 横配列 {1,2,3,4} を足し算します。
すると、Excelは自動的に「すべての組み合わせ」を計算し、4×4の2次元配列を生成します。
{1+1, 1+2, 1+3, 1+4; 2+1, 2+2, 2+3, 2+4; ...}
結果として、{2,3,4,5; 3,4,5,6; 4,5,6,7; 5,6,7,8} という、行番号と列番号の合計が詰まった4×4の配列が生まれます。

4. ISEVEN(...): ISEVEN関数が、この4×4の配列の各要素が「偶数」かどうかを判定し、TRUE/FALSEの配列に変換します。{TRUE,FALSE,TRUE,FALSE; FALSE,TRUE,FALSE,TRUE; ...}
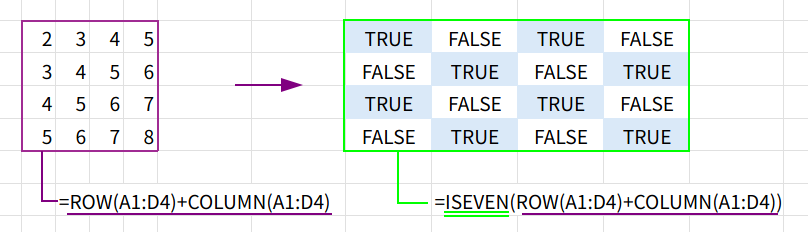
5. IF(...,"■","□"): 最後に、IF関数が、TRUEの場所を「■」、FALSEの場所を「□」に置き換えて、格子模様の完成です!

【別解】MOD関数を使う方法
=IF(MOD(ROW(A1:D4)+COLUMN(A1:D4),2)=0,"■","□")
MOD関数を使って「行+列」を2で割った「余り」が「0」かどうかを判定します。
これも、ISEVENと全く同じ結果が得られますよ!
アプローチ2:SEQUENCE + ISODD + TAKE(連番で判定)
考えかた
アプローチ1とは全く違う発想です。
まず「1, 2, 3, 4, 5…」という連番の2次元配列を作り、その数値が「奇数」か「偶数」かで塗り分けます。ただし、これにはちょっとした「罠」があります。
「なぜ、SEQUENCE(4,4)(1~16の配列)じゃダメなの?」
例えば、ISODD(SEQUENCE(4,4))だと、1行目の最後は「4」(偶数=FALSE)、2行目の最初は「5」(奇数=TRUE)となり、格子模様が正しくつながりません。
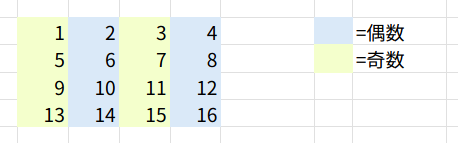
行が変わる部分で、偶数→奇数と連続してしまうからです。
格子状にするには、1行目の最後と2行目の最初が、同じ「偶数」または「奇数」である必要があります。
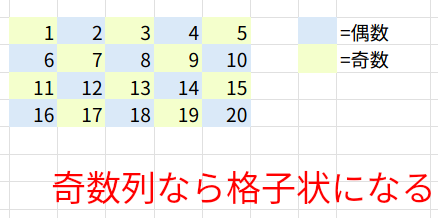
そのために、あえて「列方向に1列はみ出る形(4行5列)」で連番を作り、あとで不要な5列目を捨て去る、というテクニックを使います。
数式と解説
=IF(TAKE(ISODD(SEQUENCE(4,5)),,4),"■","□")
1. SEQUENCE(4,5): まず、4行5列の、1から20までの連番配列を生成します。
2. ISODD(...): この4×5の配列の各要素が「奇数」かどうかを判定します。
1行目の最後は「5」(奇数=TRUE)、2行目の最初は「6」(偶数=FALSE)となり、行が変わる部分の「奇数/偶数」が、うまく互い違いになる配列が作られます。

3. TAKE(..., ,4): TAKE関数は、配列から指定した行数または列数を「取り出す」関数です。
TAKE(配列, , 4)と指定することで、「配列の、先頭から4列分だけを取り出す」という意味になります。
これで、計算用に使った不要な5列目が捨てられ、欲しかった4×4のTRUE/FALSE配列が完成します。
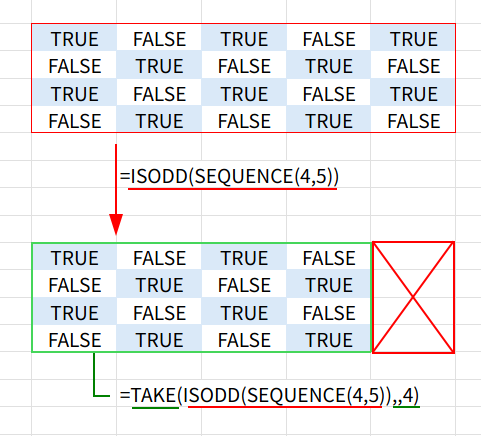
4. IF(...,"■","□"): 最後に、TRUE/FALSEを「■」と「□」に置き換えて完成です。
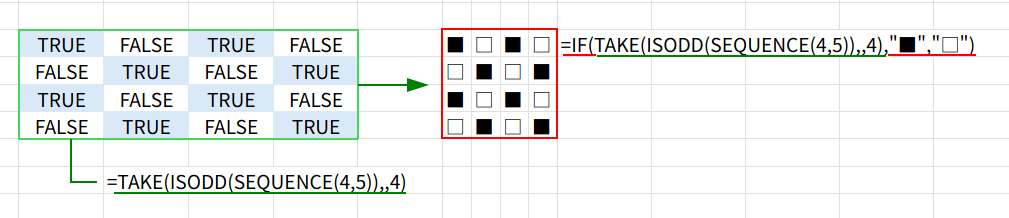
レガシー関数版(Excel 97~)
=IF(INDEX(ISODD((ROW(A1:D4)-1)*5+COLUMN(A1:E4)),ROW(A1:D4),COLUMN(A1:D4)),"■","□")
古いExcelでは、(ROW(A1:D4)-1)*5+COLUMN(A1:E4)という計算で、上記と同じ4×5の連番配列をメモリ上に作り、INDEX関数で必要な4×4の範囲だけを取り出す、というさらに複雑なことをしていました。
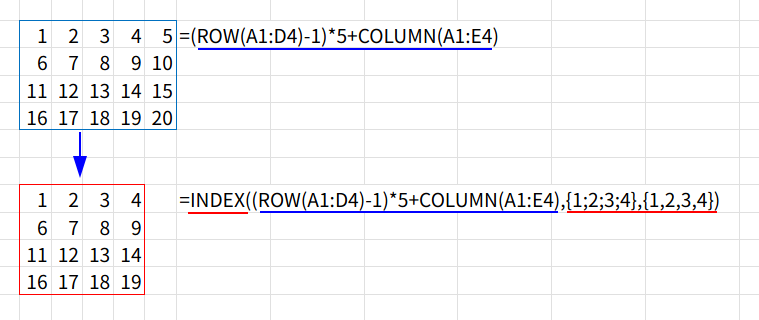
古いバージョンでは、この数式をA1セルに入力した後、A1:D4を選択した状態で「Ctrl+Shift+Enter」で配列数式として確定する必要がありました。時代は進みましたね!

アプローチ3:BITAND + SEQUENCE(0と1の配列演算)
考えかた
アプローチ1の「偶数/奇数」と似ていますが、もっと直接的に「0」と「1」の配列を作り出して、それらを演算で組み合わせて格子模様を作ります。
数式と解説
=IF((BITAND(SEQUENCE(4),1)-BITAND(SEQUENCE(,4,0),1))<>0,"■","□")
1. BITAND(SEQUENCE(4),1): BITAND関数は、数値を2進数レベルで比較します。
BITAND(数値, 1)という計算は、「数値が奇数なら1、偶数なら0を返す」という、MOD関数やISEVEN関数と同じ働きをする超高速なテクニックです。

SEQUENCE(4)(={1;2;3;4})に適用すると、{1;0;1;0}という縦配列が生まれます。
2. BITAND(SEQUENCE(,4,0),1): SEQUENCE(,4,0)で{0,1,2,3}という横配列を作り、同様にBITANDを適用すると、{0,1,0,1}という横配列が生まれます。

3. {1;0;1;0} - {0,1,0,1}: アプローチ1と同様に、縦配列と横配列の演算(今回は引き算)で、4×4の2次元配列が生成されます。{1-0, 1-1, 1-0, 1-1; 0-0, 0-1, 0-0, 0-1; ...}
結果は {1,0,1,0; 0,-1,0,-1; 1,0,1,0; 0,-1,0,-1} となります。

4. ... <> 0: この4×4の配列が「0と等しくない」かを判定します。
0の場所はFALSE、1と-1の場所はTRUEとなり、完璧な格子状のTRUE/FALSE配列が完成します。
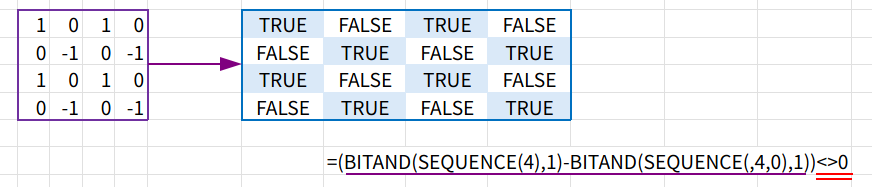
5. IF(...,"■","□"): 最後に、TRUE/FALSEを「■」と「□」に置き換えて完成です。

アプローチ4:MUNIT + HSTACK + VSTACK(行列ブロックパズル)
考えかた
これは、もはや関数パズルの極みです。
MUNIT(単位行列)関数で「1」と「0」の小さなブロックを作り、それをVSTACK(縦に積む)とHSTACK(横に積む)で組み上げて、4×4の格子模様を“建設”します。
数式と解説
=IF((HSTACK(VSTACK(MUNIT(2),MUNIT(2)),VSTACK(MUNIT(2),MUNIT(2))))=1,"■","□")
1. MUNIT(2): まず、MUNIT関数で、2×2の「単位行列」を作ります。これは {1,0;0,1} という、格子模様の最小単位(の片割れ)ですね。

2. VSTACK(MUNIT(2),MUNIT(2)): VSTACK関数で、この2×2のブロックを「縦に」2つ積みます。{1,0; 0,1; 1,0; 0,1} という、4行2列の配列ができます。
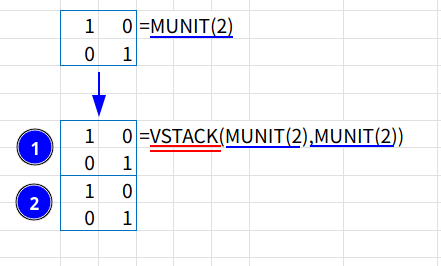
3. HSTACK(..., ...): HSTACK関数で、ステップ2で作った4×2の配列を、「横に」2つ並べます。これで、{1,0,1,0; 0,1,0,1; 1,0,1,0; 0,1,0,1} という、美しい4×4の配列が完成します。
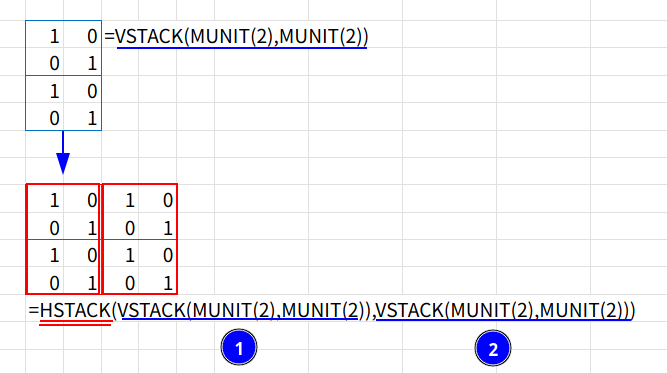
4. ... = 1: この0と1でできた配列が、「1」と等しいかどうかを判定します。1の場所がTRUE、0の場所がFALSEになります。
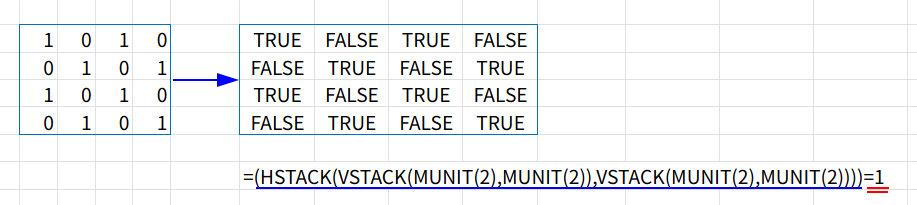
5. IF(...,"■","□"): 最後に、TRUE/FALSEを「■」と「□」に置き換えて完成です!

MUNIT関数の使い道
MUNIT関数は、本来は行列計算(線形代数)で逆行列を求めたりするのに使う、非常に専門的な関数です。
ですが、Excel関数パズル愛好家にとっては、「一瞬で『1』と『0』が規則正しく並んだ配列を作ってくれる、便利なジェネレーター」として、今回のように悪用…、応用されることがよくあります(笑)。
まとめ:格子模様への道は、一つじゃない!
一つのシンプルなゴールに対して、これほどまでに多様なアプローチが存在することに、驚かれたのではないでしょうか。
アプローチ1の「行+列」(ROW + COLUMN)が最も王道ですが、アプローチ2の「はみ出させて切り取る」発想や、アプローチ4の「ブロックを組み立てる」発想も、非常に面白いですよね。
もちろん、これ以外にも数式はたくさん作れます。
INDEX関数と組み合わせる方法など、結局は「行番号と列番号から、0か1(あるいはTRUE/FALSE)の2次元配列を作る」という、方向性に収束していくと思います。
今回の関数パズルが、皆さんの「配列脳」を鍛え、Excelの持つ無限の可能性を感じるきっかけになれば、これほど嬉しいことはありません。