はじめに：足し算と掛け算だけで、すべてを計算せよ。
「合計を出すならSUM、平均ならAVERAGE、条件付きカウントならCOUNTIF…」
私たちは普段、目的に合わせて便利な関数を使い分けています。
しかし、もしある日突然、「使えるのは行列計算（MMULT）だけ」という縛りを課せられたらどうしますか？
今回のテーマは、「MMULT関数で集計」です！
合計、累計、平均、順位、条件付き集計、さらには最大値まで。
これら7つの集計を、本来は「行列の積」を求めるための数学関数 MMULT（と、相棒の TRANSPOSE）だけで強引に解き明かします。
「え、掛け算と足し算しかできないMMULTで、なんで『順位』や『最大値』が出せるの？」
そう思ったあなたこそ、このパズルの適任者です。
この冒険を通して、Excelの奥底に眠る「行列計算」の美しさと、配列数式の無限の可能性を感じてください！
本記事では、無料のWeb版Excelを使用して検証および画像の作成を行っています。Windowsはもちろん、MacやLinuxの方もブラウザさえあれば挑戦できます！
準備：成績表の作成
何事も、まずは準備から。まっさらなシートのA1セルを起点に、以下の5人×3教科の成績表を作成してください。
={"","国語","数学","英語";"生徒A",72,58,38;"生徒B",52,44,49;"生徒C",78,47,51;"生徒D",63,74,78;"生徒E",45,94,81}
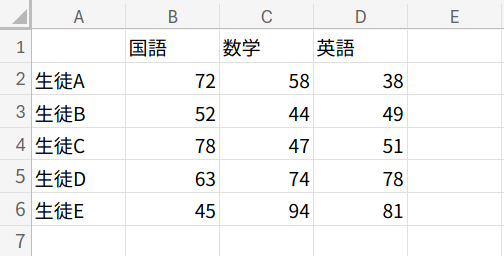
今回はロジックの理解を最優先するため、「生徒は5人」「教科は3つ」と固定して考えます。
そのため、数式の中にも {1;1;1} といった配列定数を直接書き込んでいきますよ！
そもそも、MMULT関数とは？
具体的な数式に入る前に、主役であるMMULT（エムムルト）関数について解説しましょう。
MMULTは「Matrix Multiplication（行列の積）」の略です。
2つの配列（行列）を掛け合わせるのですが、単純な掛け算ではありません。
「行と列を掛け合わせて、足し合わせる（畳み込む）」という計算を行います。
例えば、以下の数式を見てください。
=MMULT({1,2,3;4,5,6},{7,8;9,10;11,12})
これは、「2行3列」の配列と、「3行2列」の配列の掛け算です。
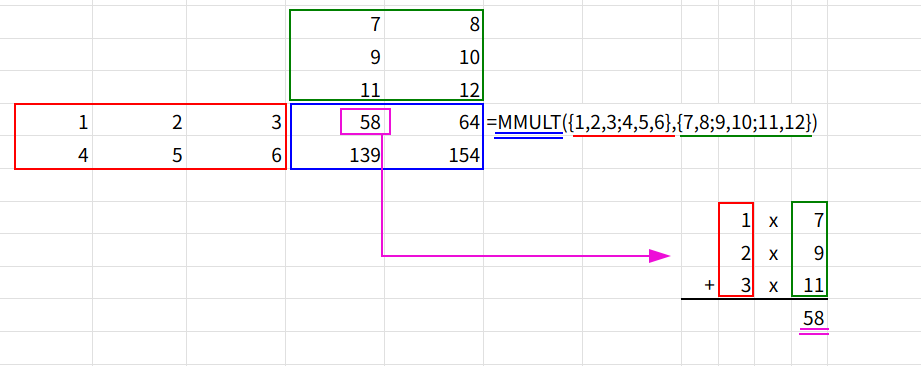
計算結果は {58,64;139,154} となります。
・1行目1列目の答え「58」は、前の行列の「1行目(1,2,3)」と、後ろの行列の「1列目(7,9,11)」をそれぞれ掛けて足したものです。（1*7 + 2*9 + 3*11 = 58）
この「掛けて、足す」という性質をうまく利用すれば、SUM関数などを使わずに集計ができるのです！
7つの集計に挑戦！
それでは、F列以降に集計結果を表示させていきましょう。「一般的な数式（フィルコピー）」と「MMULT（スピル）」を比較しながら進めます。
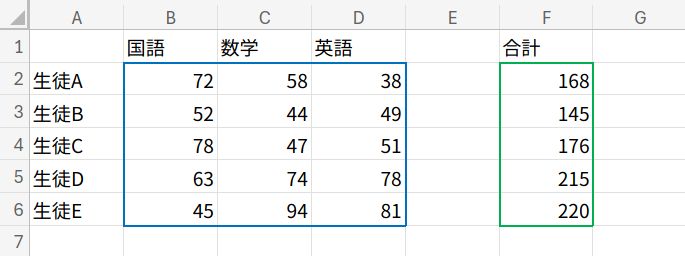
1. 合計（各生徒の3教科合計）
一般的な数式
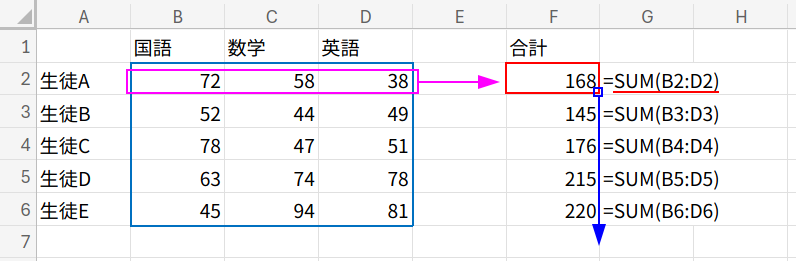
=SUM(B2:D2) （下にフィルコピー）
B2:D2（生徒Aの点数）を合計します。
下にコピーすると、B3:D3、B4:D4…と参照範囲がズレていく「相対参照」ですね。
MMULT関数（スピル）
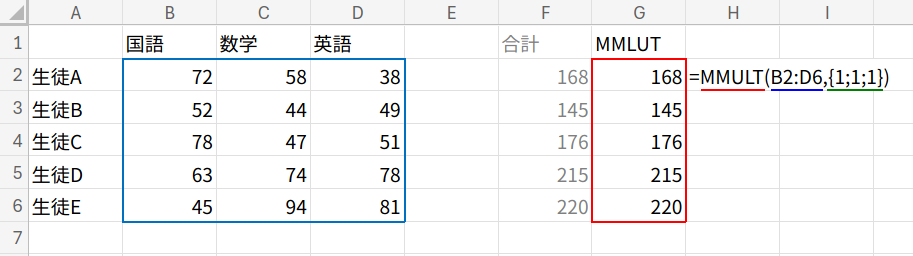
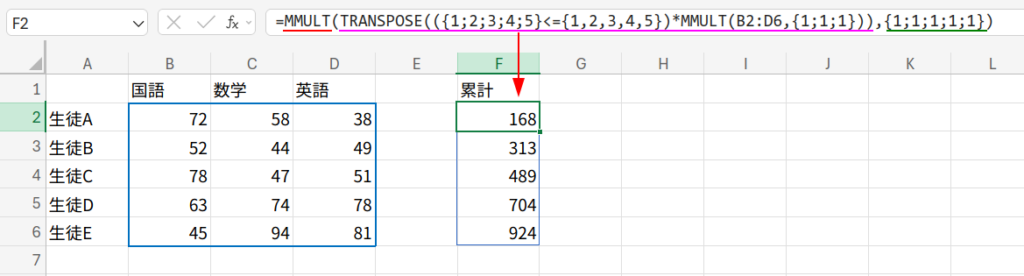
=MMULT(B2:D6,{1;1;1})
B2:D6は「5行3列」のデータです。
これに「3行1列」のすべてが1の配列 {1;1;1} を掛けます。
すると、MMULTは「1行目のデータ×1 ＋ 2列目のデータ×1 ＋ 3列目のデータ×1」という計算を全行に対して一気に行います。
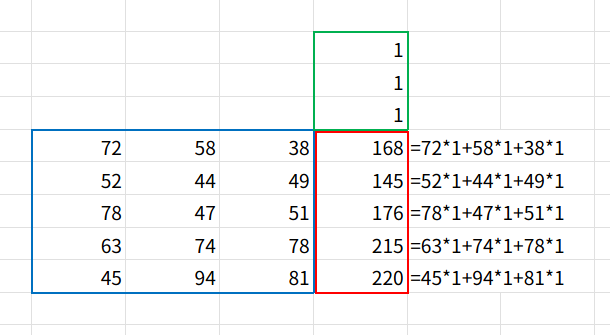
つまり、横方向の数値をすべて足し合わせる「SUM」と同じ結果になるのです！
2. 累計（合計点の累計）
一般的な数式
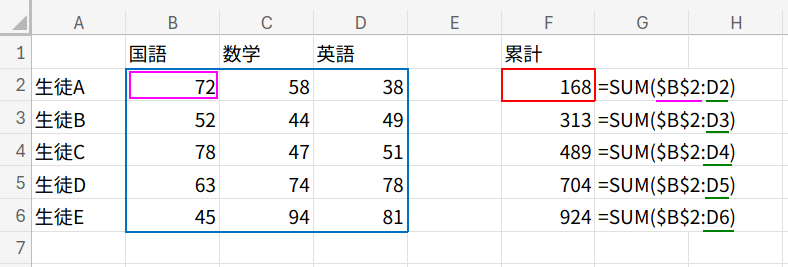
=SUM($B$2:D2)（下にフィルコピー）
始点を絶対参照（$マーク）で固定し、終点を相対参照にすることで、範囲を広げながら合計します。
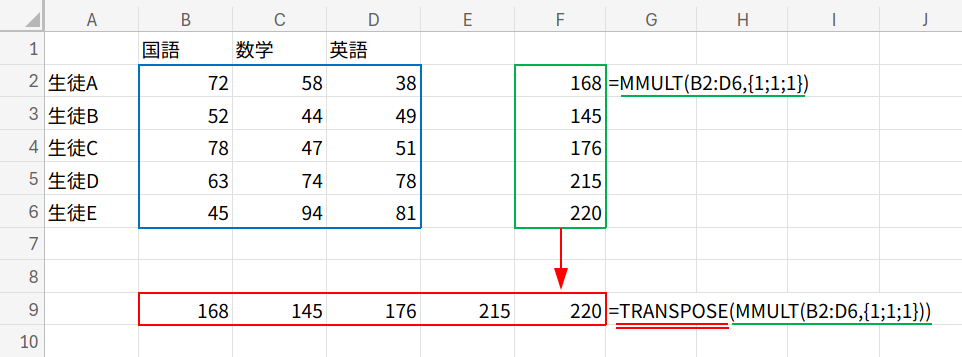
MMULT関数（スピル）
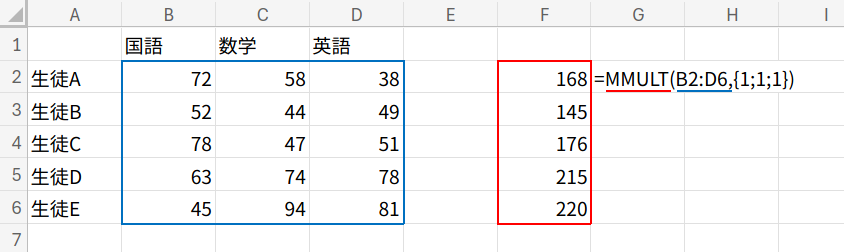
=MMULT(TRANSPOSE(({1;2;3;4;5}<={1,2,3,4,5})*MMULT(B2:D6,{1;1;1})),{1;1;1;1;1})
1. MMULT(B2:D6,{1;1;1})で、まず各生徒の合計点（5行1列）を出します。
2. {1;2;3;4;5}<={1,2,3,4,5} で、5×5の三角形のTRUE/FALSE配列（下三角行列）を作ります。
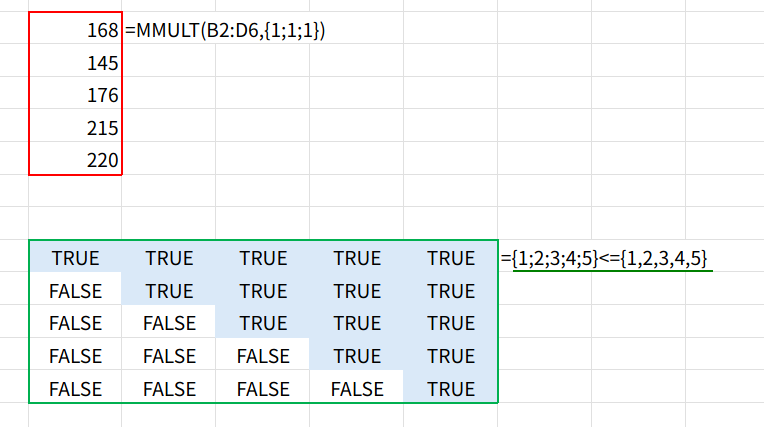
3. これらを掛け合わせ、TRANSPOSEで行列を入れ替えます。
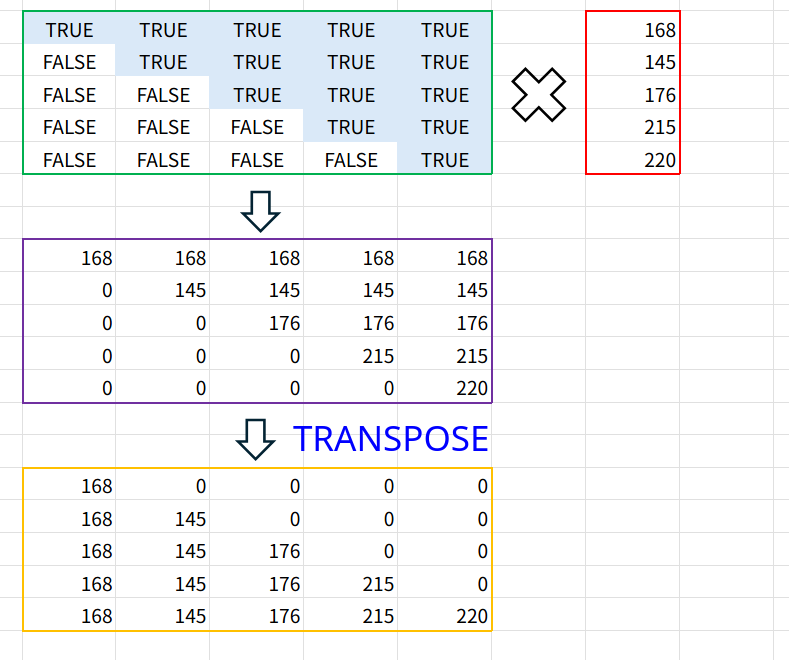
4. 最後に再びMMULTで{1;1;1;1;1}と掛けることで、上から順に足し合わせた「累計」が一発で求まります。
3. 平均（3教科の平均点）
一般的な数式
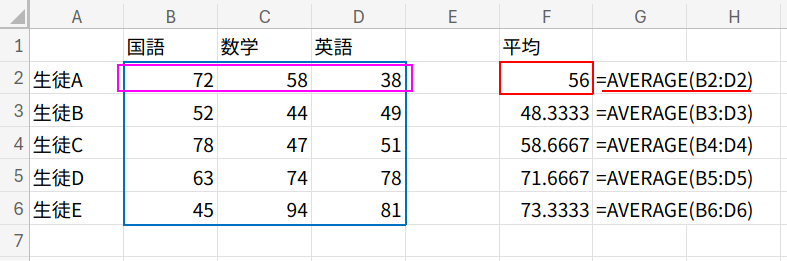
=AVERAGE(B2:D2) （下にフィルコピー）
MMULT関数（スピル）
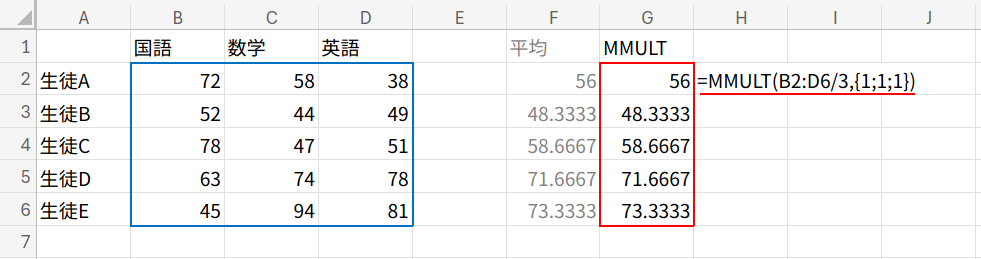
=MMULT(B2:D6/3,{1;1;1})
または、
=MMULT(B2:D6,{1;1;1})/3
平均とは「合計 ÷ 個数」のことです。
MMULTには割り算機能はありませんが、元のデータをあらかじめ3（教科数）で割っておく、あるいは最後に3で割ればいいのです。
B2:D6/3 で全ての点数を3分の1にし、それをMMULTで合計することで、結果的に「平均点」が算出されます。
4. 順位（合計点の順位）
一般的な数式
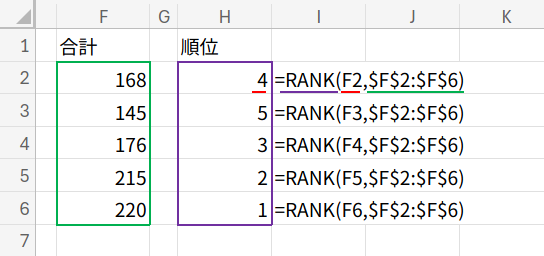
F2:F6の範囲に合計（各生徒の3教科合計）の値を入力しておきます。
=RANK(F2,$F$2:$F$6) （下にフィルコピー）
RANK関数は RANK(数値, 範囲, [順序]) のように使います。
・数値：順位を調べたい値（ここではF2）
・範囲：順位を決めるためのデータ全体（ここでは$F$2:$F$6）
指定した数値が、範囲の中で何番目に大きいかを返します。
【注意点】RANK関数に配列はNG！
RANK関数の第2引数「範囲」には、実際のセル範囲（A1:A10など）しか指定できません。
計算結果などの「配列（メモリ上のデータ）」を直接ここに入力すると、エラーになってしまいます。
=RANK(SUM(B2:D2),MMULT(B2:D6,{1;1;1}))
MMULT関数（スピル）
=MMULT((TRANSPOSE(MMULT(B2:D6,{1;1;1}))>=MMULT(B2:D6,{1;1;1}))*1,{1;1;1;1;1})
順位とは、「自分より点数が高い（または同じ）人は何人いるか？」というカウントです。
1. MMULT(...)で合計点の縦ベクトルを作ります。
2. TRANSPOSE(...)で合計点の横ベクトルを作ります。
3. この縦と横を比較（>=）することで、「AさんとBさん、どっちが上？」という総当たり戦の5×5マトリクス（勝敗表）を作ります。
それに「1」を掛けて数値化（1か0）します。
4. 最後にMMULTでその勝敗表の行ごとの「勝ち数（自分以上の人数）」を合計すれば、それがそのまま順位になります！
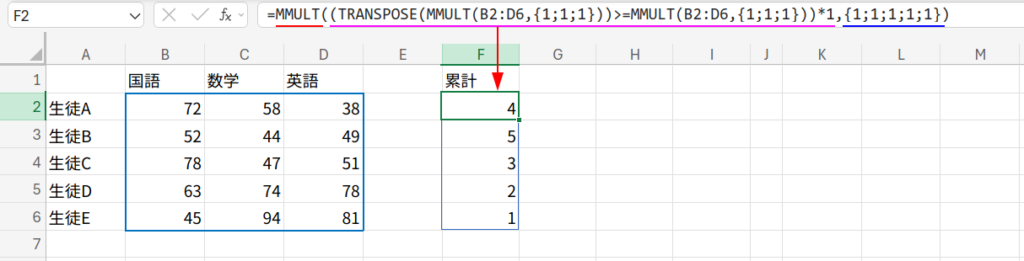
※同点がある場合の挙動はRANK関数と少し異なりますが、ロジックとしては正解です。
5. 条件付きカウント（50点以上の教科数）
一般的な数式
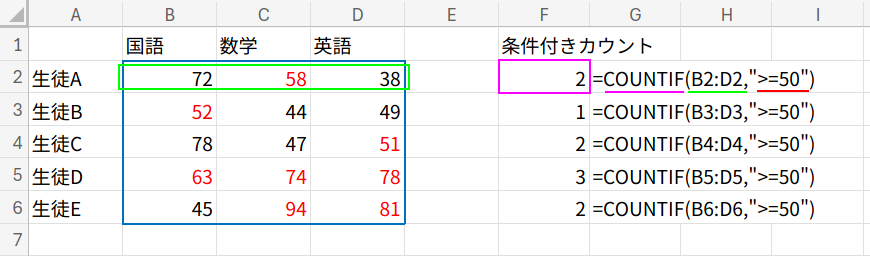
=COUNTIF(B2:D2,">=50") （下にフィルコピー）
COUNTIF関数は COUNTIF(範囲, 検索条件) のように使います。
指定した「範囲」の中から、「検索条件」（ここでは50以上）に一致するセルの個数をカウントします。
MMULT関数（スピル）
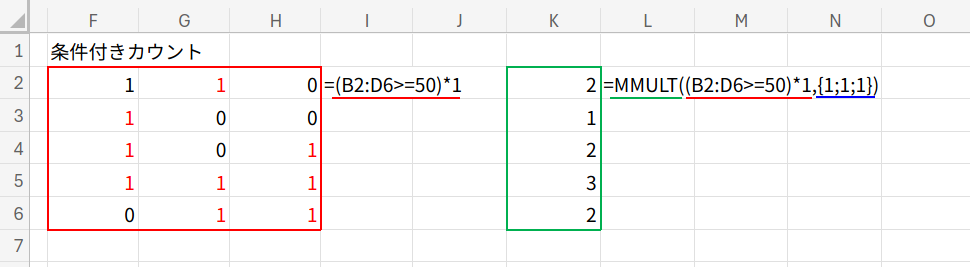
=MMULT((B2:D6>=50)*1,{1;1;1})
MMULTでカウント？
できます！
(B2:D6>=50) という条件式で、50点以上ならTRUE、未満ならFALSEの配列を作ります。
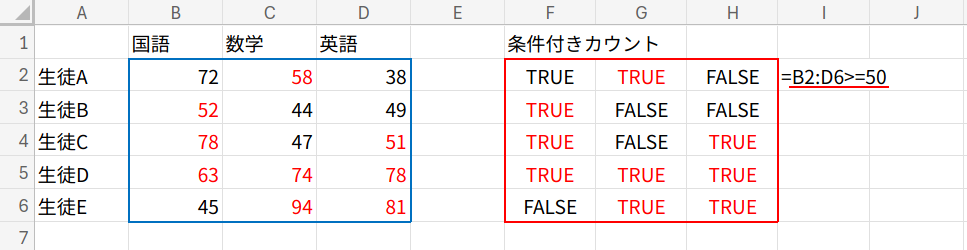
それに「1」を掛けて数値化（1か0）します。
あとは、これをMMULTで横方向に合計すれば、「1の個数 ＝ 50点以上の教科数」となります。
6. 条件付き合計（50点以上の教科だけ合計）
一般的な数式
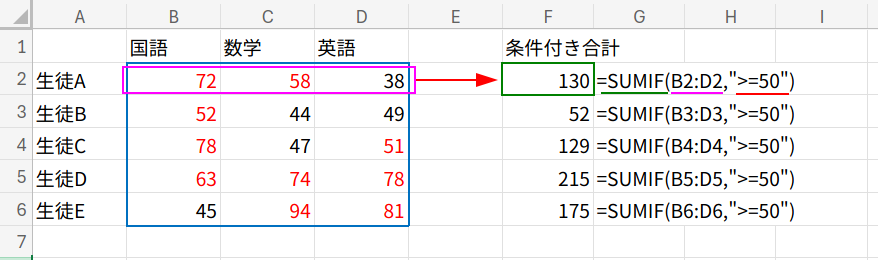
=SUMIF(B2:D2,">=50") （下にフィルコピー）
SUMIF関数は SUMIF(範囲, 検索条件, [合計範囲]) のように使います。
「範囲」の中から「検索条件」に一致するセルを探し、それに対応する「合計範囲」の値を合計します。
（合計範囲を省略した場合は、検索範囲の値を合計します。）
MMULT関数（スピル）
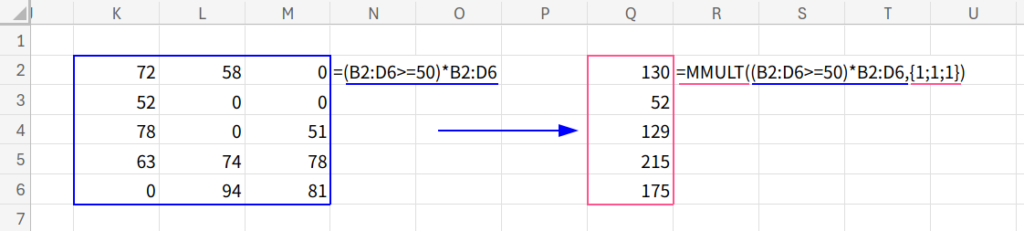
=MMULT((B2:D6>=50)*B2:D6,{1;1;1})
先程の、カウントの応用です。
(B2:D6>=50) で作った1/0の配列に、元の点数 B2:D6 を掛け算します。
すると、50点未満の場所は「0」になり、50点以上の場所だけ点数が残ります。
これをMMULTで合計すれば、条件に合う点数だけの合計（SUMIF）が完成です！
7. 最大値（各生徒の最高得点）
一般的な数式
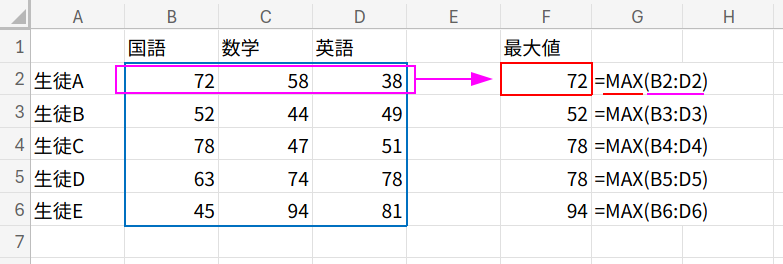
=MAX(B2:D2) （下にフィルコピー）
これは、言うまでもありませんね！
MAX関数は、複数の数値の中から 一番大きい値 を取り出す関数です。
MMULT関数（※スピル不可）
=MMULT((MMULT({1,1,1},(TRANSPOSE(B2:D2)>=B2:D2)*1)=1)*B2:D2,{1;1;1})
実は、この「最大値」（あるいは最小値）は、MMULTで一気にスピルさせることができません。
上記の数式は、1行分（B2:D2）だけを計算する数式です。これを下にフィルコピーする必要があります。
なぜ、一気にスピルできない？
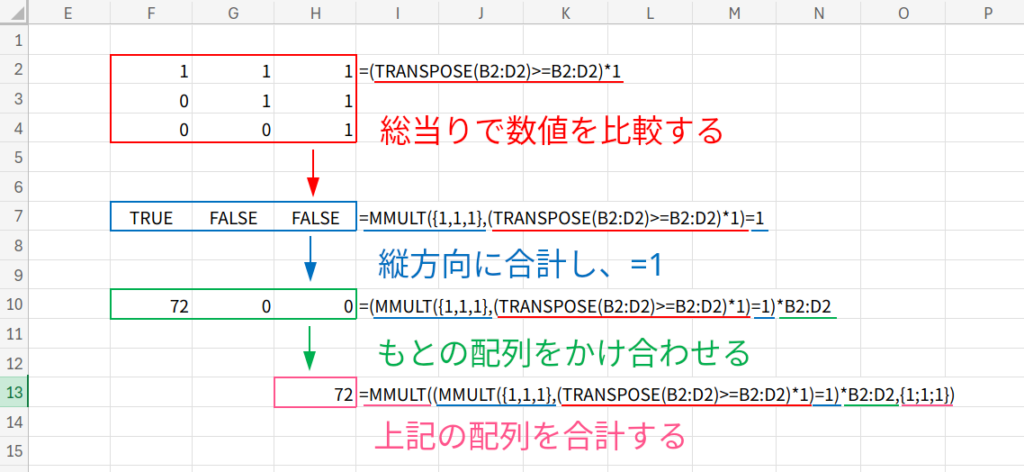
最大値を求めるには、「その行の中で、他のすべての値以上である値」を探す必要があります。
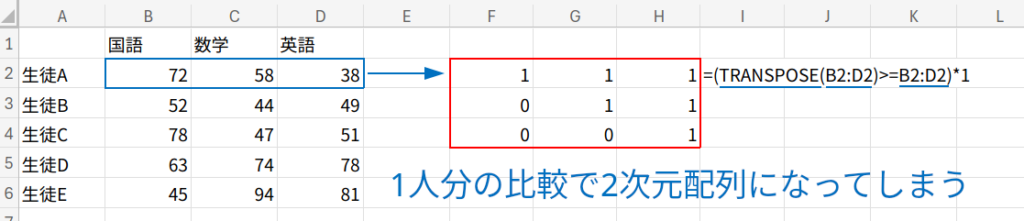
これは「3つの値同士の比較（3×3の勝敗表）」を、5人の生徒「それぞれ」に行う必要があるため、計算には「3次元」の配列が必要になってしまうのです。
Excelの数式は基本的に2次元までしか扱えないため、これを行列計算だけで一気に行うのは、次元の壁に阻まれて不可能なのです。
しかし、1行単位であれば可能です。
「自分は他の2つよりも大きいか？」という比較行列を作り、全勝している（または条件を満たす）値だけを残して合計する、という力技でMAX関数を再現しています。
まとめ：行列計算は、データの「構造」を見るメガネだ
普段何気なく使っているSUMやCOUNTIFが、実は裏側では「1と0の掛け算と足し算」で表現できるかもしれない…そう考えると、データの見え方が少し変わりませんか？
特に「最大値」の壁にぶつかった時、「関数の限界」ではなく「次元の限界」を知ることができました。これこそが、暇つぶしの醍醐味です。
実務で使うことはまずありませんが（笑）、この行列感覚は、高度なデータ分析や数式を組む時の強力な武器になるはずです！
