はじめに：その端数、5の倍数にまとめちゃいませんか？
「この数値、5円単位で切り上げたいな～」
見積書や集計表を作っていると、そんな場面によく出くわします。
例えば「123円」を「125円」に、「8円」を「10円」にするような処理です。
Excelに詳しい方なら、即座にこう答えるでしょう。
「CEILING.MATH関数を使えば一発だよ！」
はい、正解です。それが実務での最適解です。
でも、ちょっと待ってください！
もし、CEILING関数がこの世から消えてしまったら？
もし、検索関数（VLOOKUPなど）を使って、無理やり切り上げ計算をしろと言われたら？
今回の記事は、そんな「もしも」の世界を楽しむ、関数パズルです。
たった一つの「5の倍数に切り上げ」というゴールに向かって、王道から邪道、そして狂気じみた方法まで、10種類ものアプローチを紹介します。
【今回のルール】
1. ロジックの面白さを最優先するため、対象は 0以上1000以下の正の数 とします。
2. 負の数の挙動は考慮しません。（ややこしくなるので！）
この冒険を通して、Excel関数の「近似一致」の挙動や、「配列操作」のクセを深く理解できるはずです。
さあ、一緒に数字遊びを楽しみましょう！
本記事では、無料のWeb版Excelを使用して検証および画像の作成を行っています。Windowsはもちろん、MacやLinuxの方もブラウザさえあれば挑戦できます！
準備：テストデータを用意する
まずは準備です。A1セルを起点に、以下のテストデータを用意してください。
={"数値";0;0.1;4.9;5;5.1;8;10;24;101}
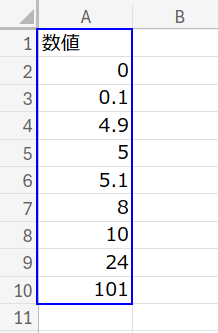
0、小数、境界値（5や10）、半端な数など、切り上げの挙動を確認するのに最適なメンバーです。
ゴールは、これらの数値をすべて「5の倍数」に切り上げること。
例えば「0.1」は「5」に、「8」は「10」になります。（0は0のままです）
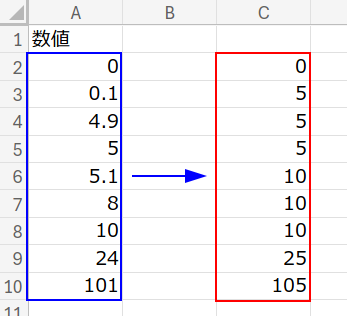
10のアプローチで、「5の倍数」を攻略せよ！
1. 王道！CEILING.MATH関数
考えかた
まずは、この処理のために生まれた専用関数から。実務ではこれを使ってください（笑）。
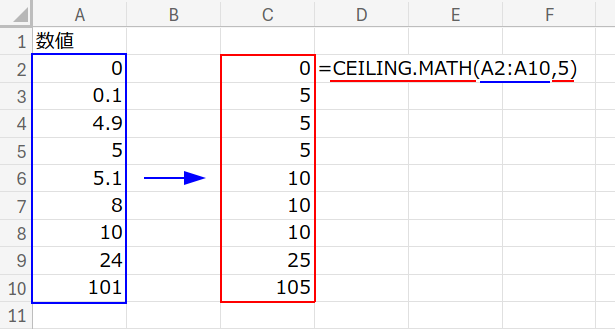
数式と解説
=CEILING.MATH(A2:A10, 5)
・CEILING（シーリング）とは「天井」のこと。数値を天井に向かって（上に向かって）丸める関数です。
・第1引数に「数値」、第2引数に「基準値（今回は5）」を指定します。
非常にシンプルで、最も処理が高速です。
2. リストに出てこない関数？ CEILING.PRECISE
考えかた
似たような関数にCEILING.PRECISEというものがありますが、環境によっては関数の候補リストに出てこないことがあります。
この記事を書いている2025/11/27現在では、無料のWEB版ExcelとMicrosoft365のダウンロード版Excelのいずれもリストに表示されません。
しかし、関数として存在はするので問題なく動作しますよ！
数式と解説
=CEILING.PRECISE(A2:A10, 5)
これは、Excelの互換性のために残されている関数です。
CEILING.MATHが登場する前のバージョンとの互換性を保つために存在しますが、基本的にはMATHを使えばOKです。
Web版ExcelやMicrosoft365のダウンロード版Excelなどでは、新しい関数への移行を促すために、あえてリストから隠されているのかもしれませんね。
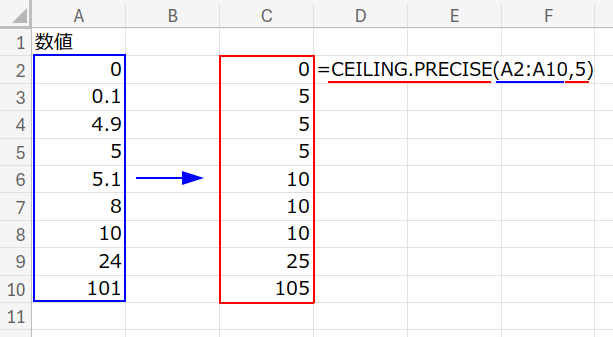
3. 普通の切り上げを応用 (ROUNDUP)
考えかた
「5の倍数にする」ということは、「5で割った世界で整数にする」ということです。
大雑把に言うと…。
数式と解説
=ROUNDUP(A2:A10/5, 0)*5
1. A2:A10/5: まず数値を5で割ります。（例：8 ÷ 5 = 1.6）
2. ROUNDUP(..., 0): その結果を、小数第1位で切り上げます。（1.6 → 2）
3. ... * 5: 最後に5を掛けて元の世界に戻します。（2 × 5 = 10）
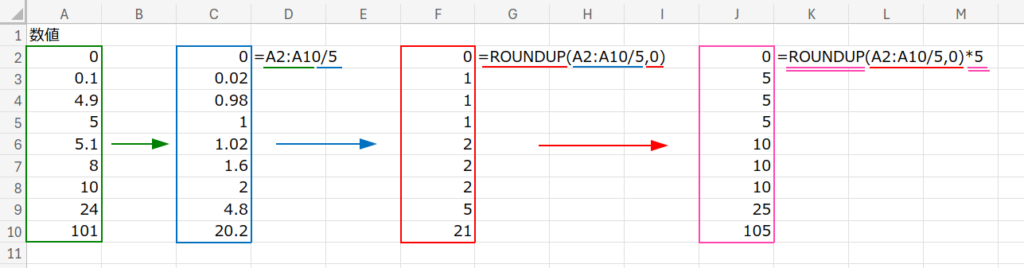
数学的で美しい、非常に汎用性の高い考え方です。
4. 商と余りを利用 (QUOTIENT + MOD)
考えかた
「割り算の商（QUOTIENT）」と「余り（MOD）」を使って、手動で切り上げロジックを組みます。
数式と解説
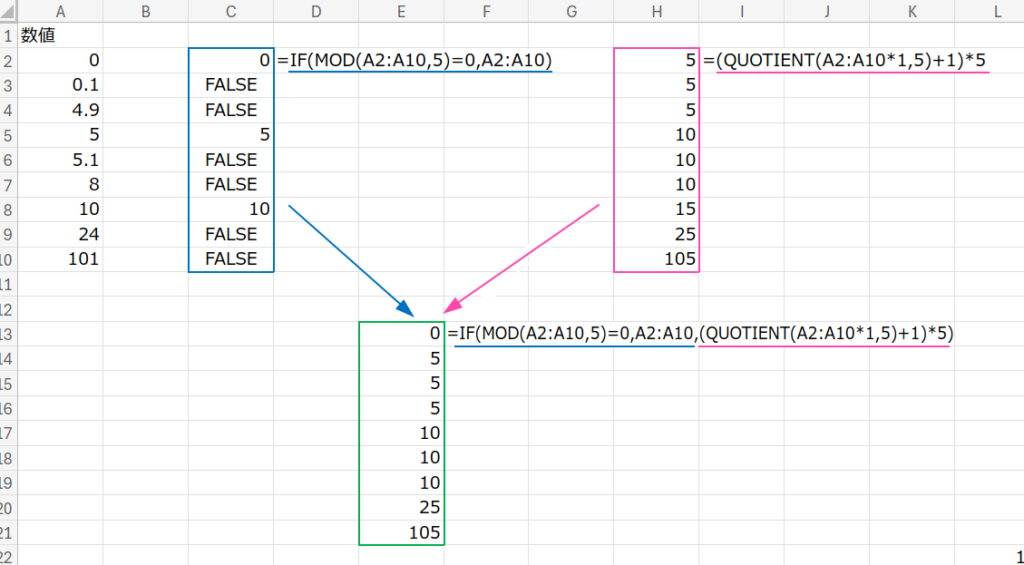
=IF(MOD(A2:A10,5)=0,A2:A10,(QUOTIENT(A2:A10*1,5)+1)*5)
・IF(MOD(...,5)=0, ...): まず、5で割り切れる（余りが0）なら、そのままの数値を返します。
・(QUOTIENT(A2:A10*1,5)+1)*5: 割り切れない場合、「商」に1を足して5を掛けます。
例：8÷5の商は1 → 1+1=2 → 2×5=10
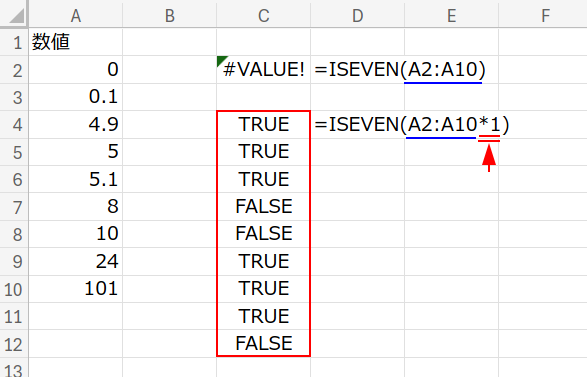
【重要ポイント！】なぜ「*1」してるの？
QUOTIENT(A2:A10*1, 5) の部分に注目してください。
実は、QUOTIENT関数はそのまま配列（範囲）を渡してもうまく計算してくれないことがあります。
そこで、*1 をして計算を挟むことで、Excelに「これは単なるセル範囲じゃなくて、数値の配列データだよ！」と強制的に認識させています。
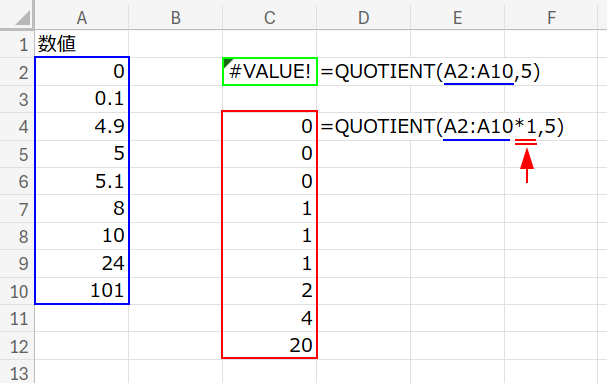
ISEVEN関数などでも使う、必須テクニックです！
5. IFを使った条件分岐
考えかた
「あといくつ足せば5の倍数になるか？」を計算して足します。
数式と解説
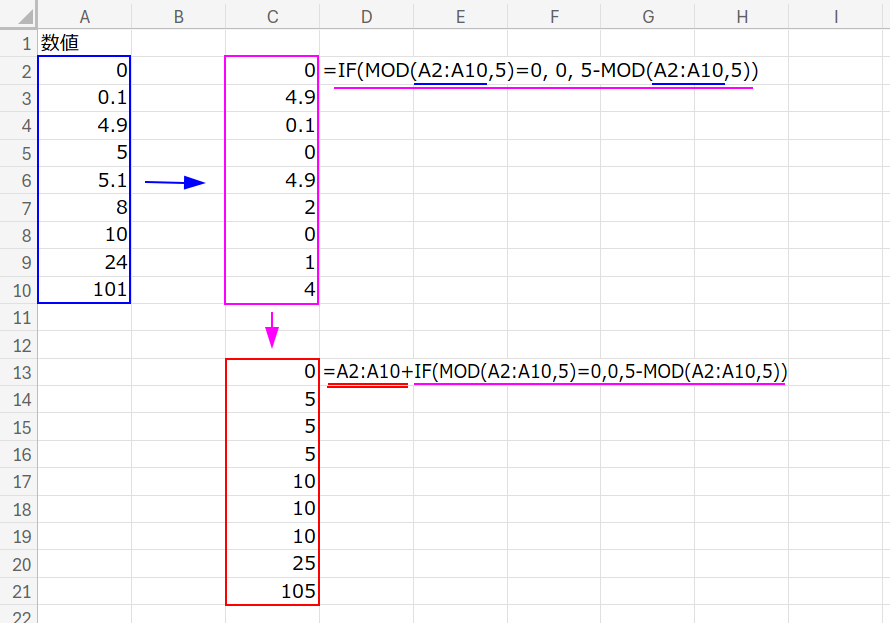
=A2:A10 + IF(MOD(A2:A10,5)=0, 0, 5-MOD(A2:A10,5))
・割り切れるなら、何も足しません（+0）
・割り切れないなら、「5 – 余り」を足します。
（例：8を5で割った余りは3。あと「5-3=2」足せば10になりますよね！）
6. MOD関数のみで切り上げる！
考えかた
IF関数すら使わず、論理値（TRUE/FALSE）の計算だけで条件分岐を実現します。
数式パズルの世界へようこそ！
数式と解説
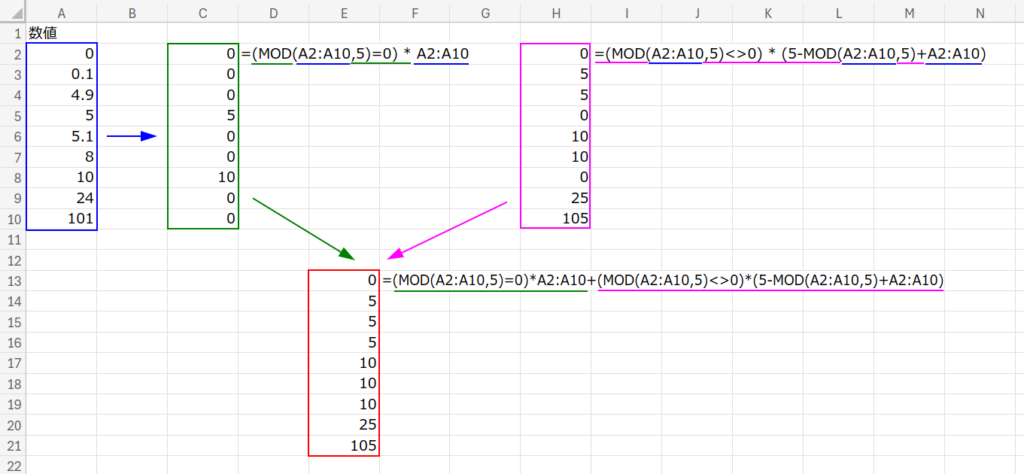
=(MOD(A2:A10,5)=0)*A2:A10 + (MOD(A2:A10,5)<>0)*(5-MOD(A2:A10,5)+A2:A10)
この数式は一見複雑ですが、実は「スイッチ」の仕組みになっています。
数式を大きく2つのパートに分けて考えてみましょう。
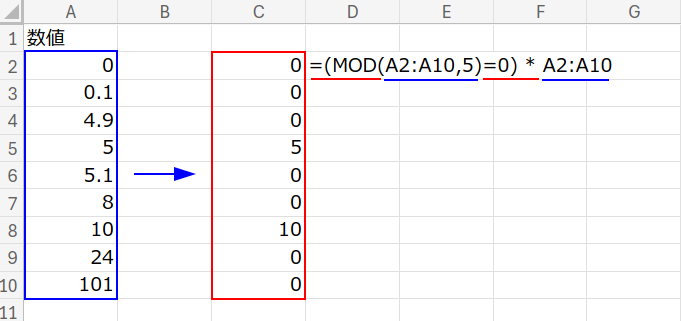
パート1：割り切れる場合の計算
(MOD(A2:A10,5)=0) * A2:A10
・MOD(...,5)=0: もし5で割り切れるならTRUE（1）、割り切れないならFALSE（0）になります。
・... * A2:A10: それに元の数値を掛けます。
・割り切れる時：1 * 数値 = 数値（そのまま）
・割り切れない時：0 * 数値 = 0（消える！）
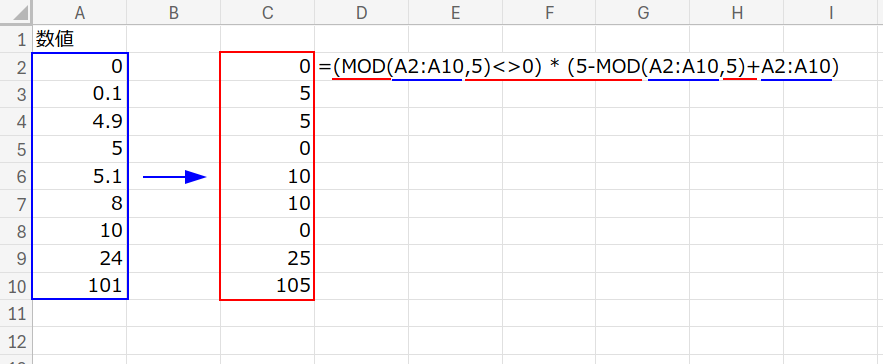
パート2：割り切れない場合の計算
(MOD(A2:A10,5)<>0) * (5-MOD(A2:A10,5)+A2:A10)
・MOD(...,5)<>0: もし5で割り切れないならTRUE（1）、割り切れるならFALSE（0）になります。
・... * (...): それに「計算式」を掛けます。
・割り切れる時：0 * (計算式) = 0（消える！）
・割り切れない時：1 * (5 - 余り + 元の数値)
（例：8の場合 → 5 – 3 + 8 = 10）
結論：
この2つのパートを足し合わせると、どちらか一方は必ず「0」になり、もう一方だけが「答え」になります。
「(AのスイッチONならA) ＋ (BのスイッチONならB)」 という仕組みで、IF関数を使わずに分岐を実現しているのです！
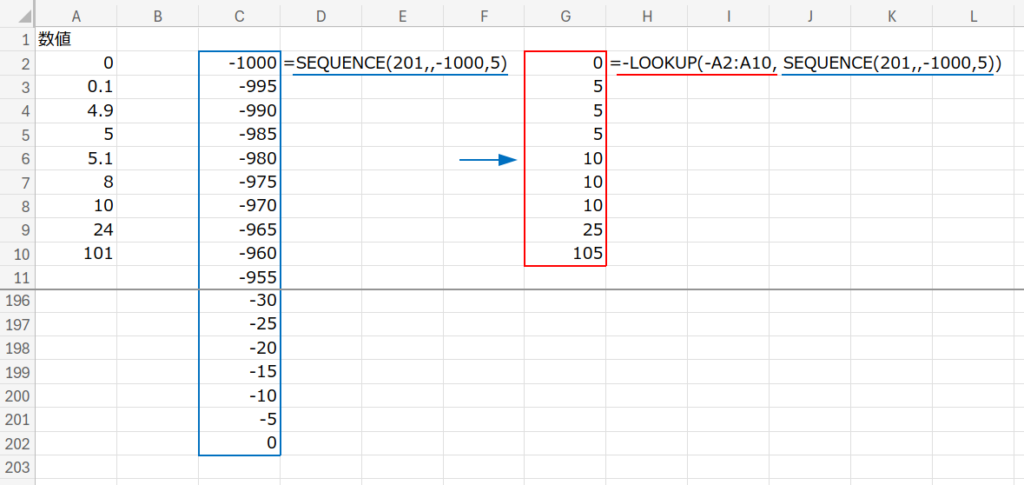
7. MATCH関数 (検索で切り上げ！？)
考えかた
ここからは検索系関数の出番です。
「0, 5, 10, 15…」という5の倍数のリストを用意し、そこから目的の数値を探し出します。
しかし、普通の検索（近似一致）は「その数値以下」を探してしまいます（切り捨て）。
「切り上げ」にするにはどうすれば…？
答え：「マイナスの世界」に行けばいいんです！
数式と解説
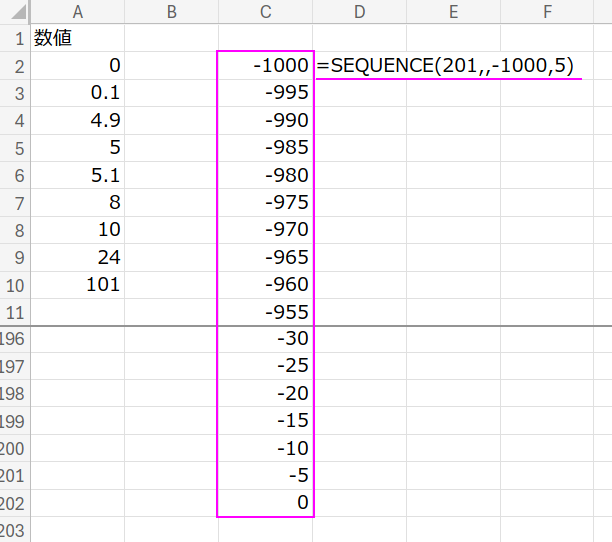
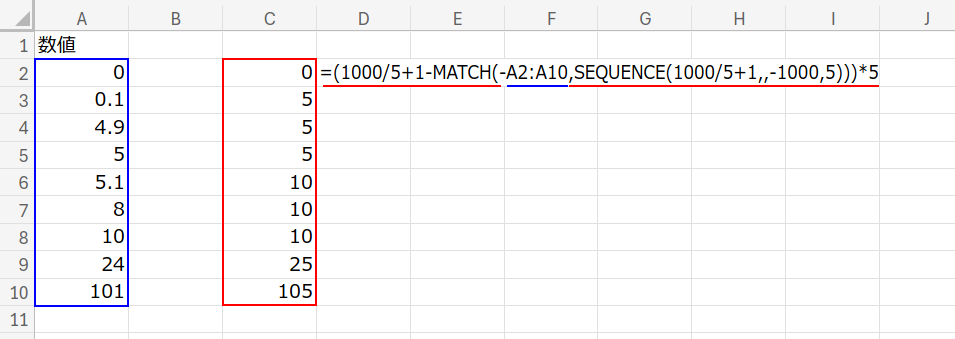
=(1000/5+1 - MATCH(-A2:A10, SEQUENCE(1000/5+1,,-1000,5))) * 5
このロジックは少々難解です。段階を追って解説します。
1. 連番の作成: SEQUENCE(201,,-1000,5)
これで、{-1000, -995, ..., -10, -5, 0} という、昇順に並んだ負の5の倍数リストを作ります。
2. マイナスで検索: MATCH(-A2:A10, ...)
例えば「8」を切り上げたい場合、「-8」で検索します。
MATCH（近似一致）は、「-8」以下で最大の数値を探します。
このリストの中で「-8」以下で最大なのは…「-10」です！
※「-5」は「-8」より大きいので選ばれません。ここがポイント！
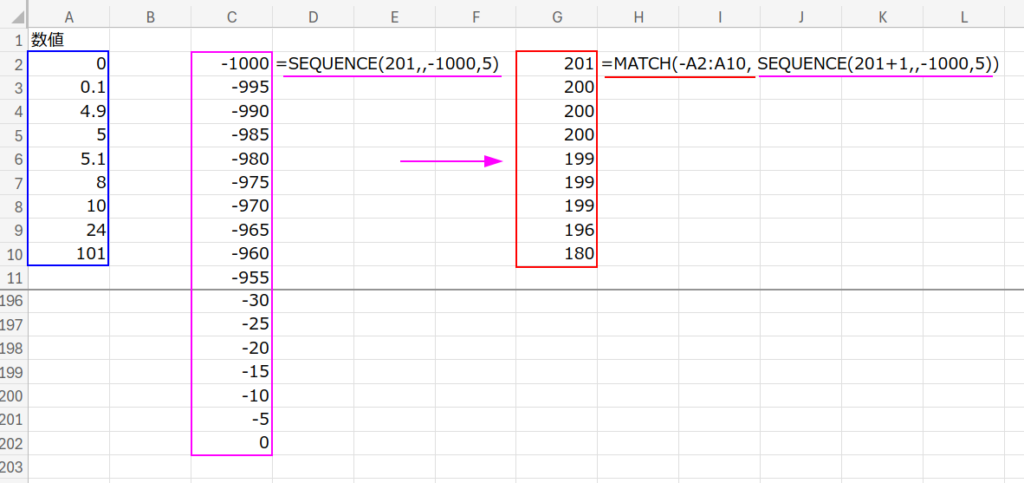
3. 位置の特定: MATCHは「-10」がリストの何番目にあるかを返します。
4. 計算で戻す: その位置情報を使って、元の正の数の世界での「10」を導き出します。
「切り下げ（以下）」の挙動しか持たない関数でも、マイナスの世界に行けば「切り上げ（以上）」の挙動になる。
この逆転の発想こそが、Excelパズルの醍醐味です！
8. 検索の古典派 LOOKUP
考えかた
MATCHと同じ「マイナスの世界」のロジックを、LOOKUP関数で実装します。
数式と解説
=-LOOKUP(-A2:A10, SEQUENCE(201,,-1000,5))
LOOKUP関数も、データが昇順であれば「近似一致（以下の最大値）」を返します。
1. SEQUENCEで{-1000, ..., -5, 0}を作成。
2. 「8」を「-8」にして検索。
3. 「-8」以下の最大値である「-10」がヒットして返ってきます。
4. 最後に先頭のマイナス-LOOKUPで、「-10」を「10」に戻します。
これなら数式も短くてスッキリしますね！
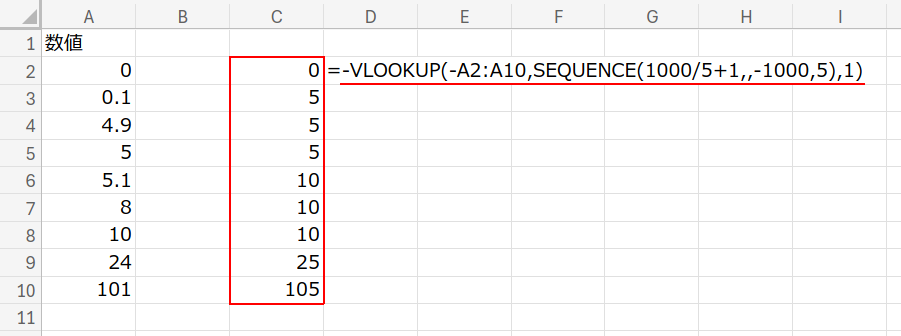
9. 意地でもVLOOKUPでやりたい！
考えかた
「私はVLOOKUPしか信じない！」という方のための数式です。
LOOKUPとほぼ同じですが、引数指定が少し面倒です。
数式と解説
=-VLOOKUP(-A2:A10, SEQUENCE(201,,-1000,5), 1)
VLOOKUPの第4引数を省略（TRUE）にすると、近似一致になります。
ロジックはLOOKUPと全く同じです。
わざわざVLOOKUPで5の倍数に切り上げる…なんだかロマンを感じませんか？
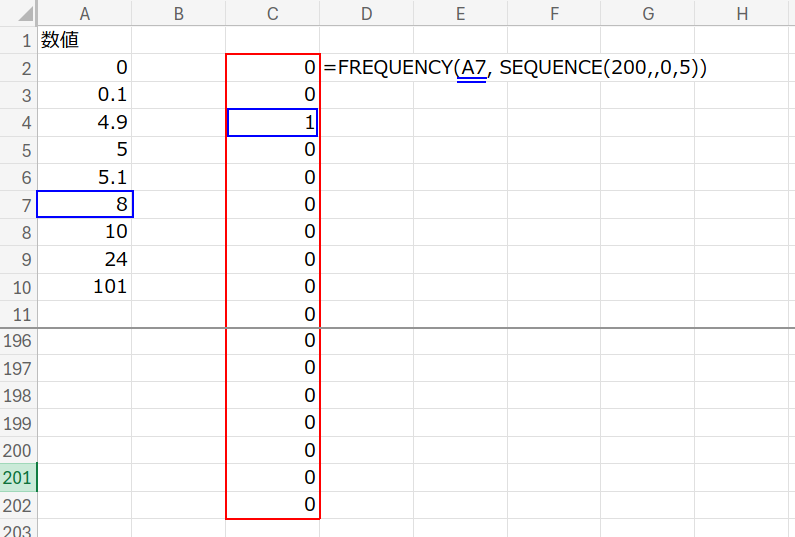
10. 最後は、度数分布のFREQUENCY
考えかた
当ブログでおなじみ、度数分布の専門家FREQUENCY関数の登場です！
使用方法などは、Excel FREQUENCY関数 スピルで覚醒！で、詳しく解説しています。
数式と解説
=SUM(FREQUENCY(A2, SEQUENCE(200,,0,5)) * SEQUENCE(201,,0,5))
※この数式だけは、A2セル単体に対する計算です。スピルしませんので、下にフィルコピーしてください。
1. SEQUENCE(200,,0,5): {0, 5, 10...}という「区切り値」を作ります。
2. FREQUENCY(A2, ...): 数値A2が、どの区間に入るかを判定します。
該当する区間の場所だけが「1」、他は「0」になる配列が返ってきます。
（例：A7が8なら、5～10の区間に「1」が立ちます）
3. ... * SEQUENCE(...): その「1」が立った場所に、対応する5の倍数の値を掛け算します。
4. SUM(...): 最後に合計して取り出します。
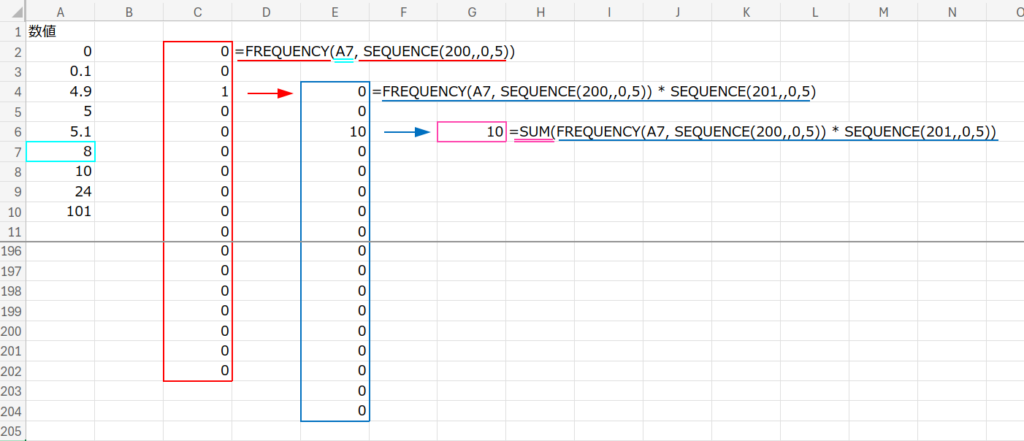
やっていることは、はっきり言って無駄です（笑）。
しかし、「どの箱に入るか？」という判定を使って数値を丸めるという発想は、完全に関数パズルの世界です。
まとめ：答えは一つじゃない！
たった一つのシンプルな計算でも、CEILING関数だけでなく、割り算、検索、そしてマイナスの世界への反転など、実に10通りものアプローチがありました。
実務では迷わず CEILING.MATH を使ってください。
でも、もし頭の体操をしたくなったら、ぜひ MATCH や LOOKUP で切り上げに挑戦してみてください。
その回り道が、あなたのExcel脳を鍛え、もっと複雑な問題を解決する時のヒントになるはずです！
