はじめに：Excelは「数学」も得意なんです。
学生時代、数学の時間にやった「素因数分解」。
覚えていますか？
例えば、「12」なら 
（つまり 
）
ある整数を、素数の掛け算の形に分解することです。
「これをExcelでやりたい！」と思った時、普通ならVBA（マクロ）を使ってプログラムを書くところです。
でも、それじゃあ面白くないですよね？
今回のテーマは、「関数（数式）だけで素因数分解をする！」です。
使う数式は、たったの3つ。
最新のExcel関数をフル活用して、複雑な計算ロジックを美しく組み立てていきます。
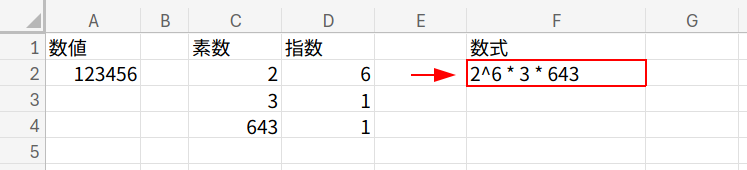
【今回のゴール】
A2セルに、例えば「2646」と入力したら、F2セルに 2 * 3^3 * 7^2 と表示させること！
パズルを解くような気持ちで、Excelの奥深い世界を楽しんでください！
本記事では、無料のWeb版Excelを使用して検証および画像の作成を行っています。Windowsはもちろん、MacやLinuxの方もブラウザさえあれば挑戦できます！
ステップ1：冒険の準備
まずは準備です。まっさらなシートを用意しましょう。
1. A1セルに「数値」、
A2セルに分解したい数値を入力します。
今回は例として「2646」を入力してみましょう。
2. C1セルに「素数」、D1セルに「指数」と見出しをつけておきます。
さあ、ここからが本番です！
ステップ2：割り切れる「素数」を見つけ出せ！
最初のミッションは、2646を割り切ることができる「素数」のリストを作ることです。
2646の場合、正解は 2, 3, 7 の3つです。
C2セルに、以下の数式を入力してください。
今回はロジックを分かりやすくするため、数式の中で日本語の変数名を使っています！
数式1：素数抽出のロジック
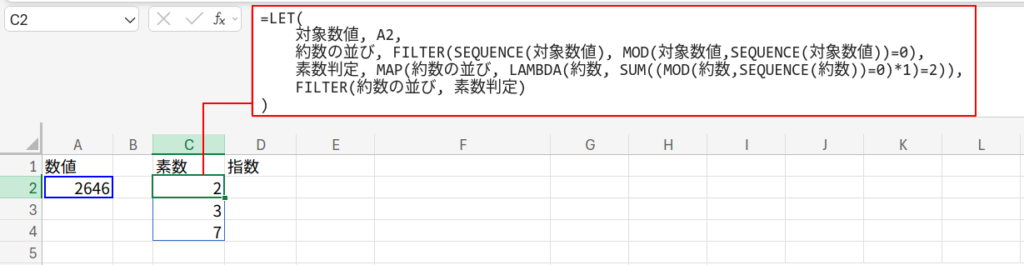
=LET(
対象数値, A2,
約数の並び, FILTER(SEQUENCE(対象数値), MOD(対象数値,SEQUENCE(対象数値))=0),
素数判定, MAP(約数の並び, LAMBDA(約数, SUM((MOD(約数,SEQUENCE(約数))=0)*1)=2)),
FILTER(約数の並び, 素数判定)
)
うーん、長いですね！
でも、LET関数のおかげで、意味ごとのブロックに分かれています。
順を追って解読しましょう。
ロジックの詳細解説
1. 「約数の並び」を作る
FILTER(SEQUENCE(対象数値), MOD(対象数値,SEQUENCE(対象数値))=0)
この部分はさらに細かく分解できます。
SEQUENCE(対象数値): まず、1から対象数値（2646）までの膨大な連番 {1, 2, 3, ..., 2646} を作ります。
MOD(対象数値, SEQUENCE(...)): 2646を、その連番ひとつひとつで割り算し、余りを計算します。
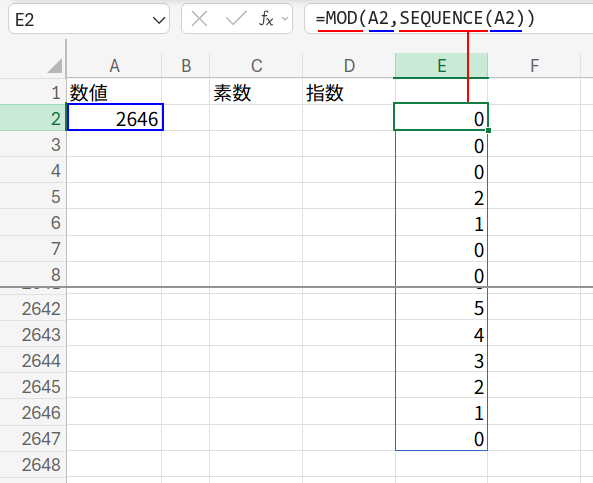
...=0: 余りが「0」であるか（割り切れるか）を判定し、TRUE/FALSEの配列を作ります。
FILTER(連番, ...): 割り切れた数（TRUEの場所）だけを取り出します。
これで、2646の「約数リスト」が完成します。（例：1, 2, 3, 6, 7, 9… 2646）
2. 「素数判定」を行う
ここが最難関ポイントです！
MAP(約数の並び, LAMBDA(約数, SUM((MOD(約数,SEQUENCE(約数))=0)*1)=2)),
FILTER(約数の並び, 素数判定)
【関数の解説：MAPとLAMBDA】
・MAP(配列, LAMBDA(変数, 計算式)): 配列に入っているデータ一つひとつに対して、同じ処理（計算）を繰り返し行いたい時に使います。
・LAMBDA(変数, 計算式): その「繰り返したい処理の中身」を定義する関数です。ここでは「約数」という名前の変数を受け取って、それが素数かどうかを計算する式を定義しています。
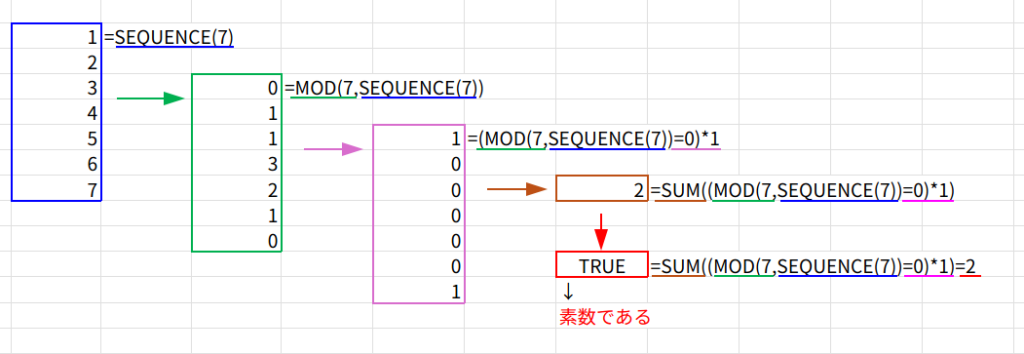
LAMBDAの中身の式：SUM((MOD(約数,SEQUENCE(約数))=0)*1)=2
SEQUENCE(約数): その約数（例えば「7」）までの連番 {1, 2, ... 7} を作ります。
MOD(...): 7を連番で割り、余りを求めます。
SUM(...=0): 割り切れた回数（約数の個数）をカウントします。
「7」なら1と7で割り切れるので、個数は「2」です。
...=2: 約数の個数がちょうど2個（1と自分自身）であれば、それは「素数」です！
3. 最後に「FILTER」
FILTER(約数の並び, 素数判定)
最初の約数リストの中から、MAP関数による判定が「TRUE（素数である）」だったものだけを残します。
この数式を確定すると、C2セル以下に 2, 3, 7 がスピル（自動展開）されます！
ステップ3：何回割れる？「指数」を計算せよ！
素数が見つかったら、次は「その素数で何回割り切れるか（指数）」を調べます。
・2では1回割れる（
）
・3では3回割れる（
）
・7では2回割れる（
）
この「1, 3, 2」という数値を導き出します。
D2セルに、以下の数式を入力してください。
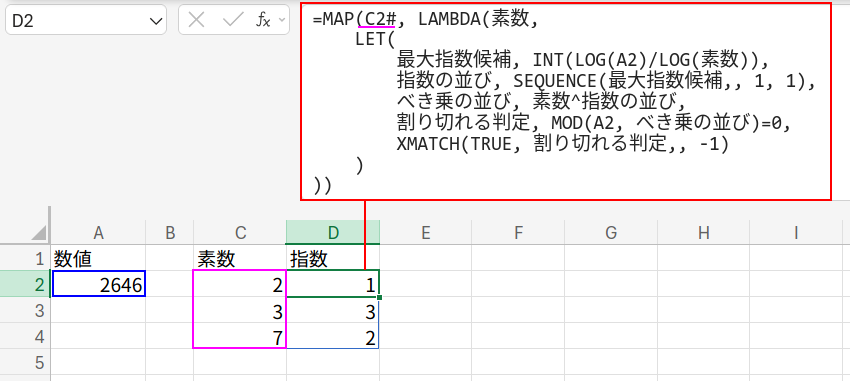
数式2：指数算出のロジック
=MAP(C2#, LAMBDA(素数,
LET(
最大指数候補, INT(LOG(A2)/LOG(素数)),
指数の並び, SEQUENCE(最大指数候補,, 1, 1),
べき乗の並び, 素数^指数の並び,
割り切れる判定, MOD(A2, べき乗の並び)=0,
XMATCH(TRUE, 割り切れる判定,, -1)
)
))
これもパズルのような美しさです！
MAP(C2#, ...) で、C列に出した素数リスト（2, 3, 7）のそれぞれに対して計算を行います。
ロジックの詳細解説
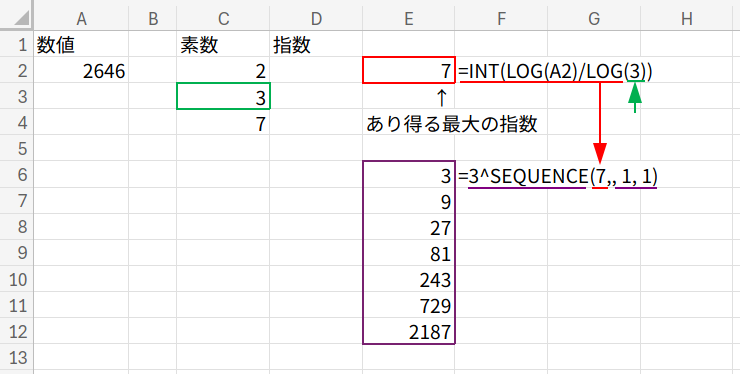
1. 「最大指数候補」を見積もる
INT(LOG(A2)/LOG(素数))
例えば 
となる 
はいくつか？というのを対数（LOG）を使って計算し、あり得る最大の指数（回数）を見積もります。
2. 「べき乗の並び」を作って総当たり
SEQUENCE で指数の候補を作り、^ でべき乗します。
例えば素数が「3」の場合、3^1, 3^2, 3^3, 3^4... という「3の累乗リスト（3, 9, 27, 81…）」を作ります。
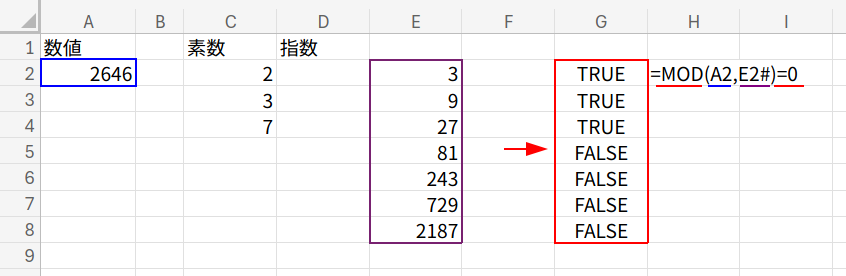
3. 「割り切れる判定」と「XMATCH」
MOD(A2, べき乗の並び)=0
元の数値(2646)を、この累乗リストで割ってみます。
・2646 ÷ 
(3) = 割り切れる (TRUE)
・2646 ÷ 
(9) = 割り切れる (TRUE)
・2646 ÷ (27) = 割り切れる (TRUE)
・2646 ÷ 
(81) = 割り切れない (FALSE)
XMATCH(TRUE, 割り切れる判定,, -1)
【関数の解説：XMATCH】
・XMATCH(検索値, 検索範囲, [一致モード], [検索モード]): MATCH関数の進化版です。
・第4引数の「検索モード」に「-1」を指定すると、後ろから（末尾から先頭へ）検索を行います。
今回はこれを利用して、「割り切れる（TRUE）」の中で一番後ろにあるもの（＝最大の指数）の位置を特定しています。ここでは3番目の「3」が見つかりますね。
これで、D列に 1, 3, 2 が表示されました。
ステップ4：美しく数式として「連結」する
最後に、バラバラになった「素数（C列）」と「指数（D列）」を、見慣れた数学の形に整形します。
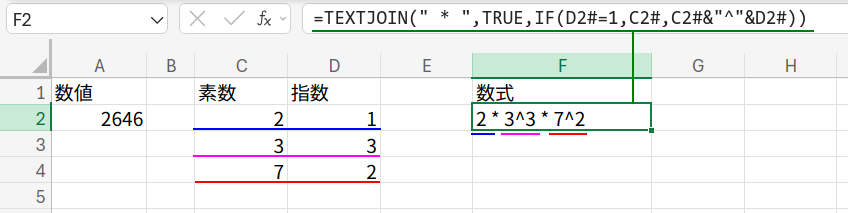
F2セルに、以下の数式を入力します。
数式3：テキスト整形のロジック
=TEXTJOIN(" * ",TRUE,IF(D2#=1,C2#,C2#&"^"&D2#))
ここはExcel初心者の方にも覚えてほしいテクニックです！
1. 指数が「1」のときは省略する
IF(D2#=1, C2#, C2#&"^"&D2#)
数学では とは書かず、単に 
と書きますよね。
なので、「もし指数が1なら素数そのまま、そうでなければ『素数^指数』の形にする」という条件分岐を入れています。（& は文字をつなげる記号です！）
2. 「 * 」でつなぐ
TEXTJOIN(" * ", TRUE, ...)
最後に、それらのパーツを " * " という区切り文字で連結します。
見やすいように、アスタリスクの前後に半角スペースを入れているのが、筆者のこだわりポイントです。
まとめ：ロジックを組む楽しさ
一見すると複雑な計算も、「素数を見つける」「回数を数える」「文字にする」と分解していけば、Excelの関数だけで十分に実現できることが分かりました。
特に LET や MAP といった最新関数を使うことで、まるでプログラミングのようにロジックを記述できるのが、現代Excelの醍醐味です。
【ちょっと一言：素因数分解って何の役に立つの？】
「で、これをやって何になるの？」と思うかもしれません。
実務での直接的な出番は少ないですが、素因数分解は「暗号技術（RSA暗号など）」の基礎となっている重要な考え方です。巨大な数を素因数分解するのがものすごく大変であることを利用して、私たちのインターネット通信は守られているのです。
Excelでその一端に触れるのも、面白い暇つぶしだと思いませんか？
ぜひ、A2セルの数字を「123456」や、あなたの好きな数字に変えて遊んでみてください。
（ちなみに 123456 は 2^6 * 3 * 643 になりますよ！）
