はじめに:Excelの限界に挑戦しよう。
突然ですが、問題です。
![]() (2の100乗)は、いくつになりますか?
(2の100乗)は、いくつになりますか?
手元の電卓アプリ(Windows, Mac, Linuxなど)で計算してみると、すぐに答えが出ます。
「1,267,650,600,228,229,401,496,703,205,376」
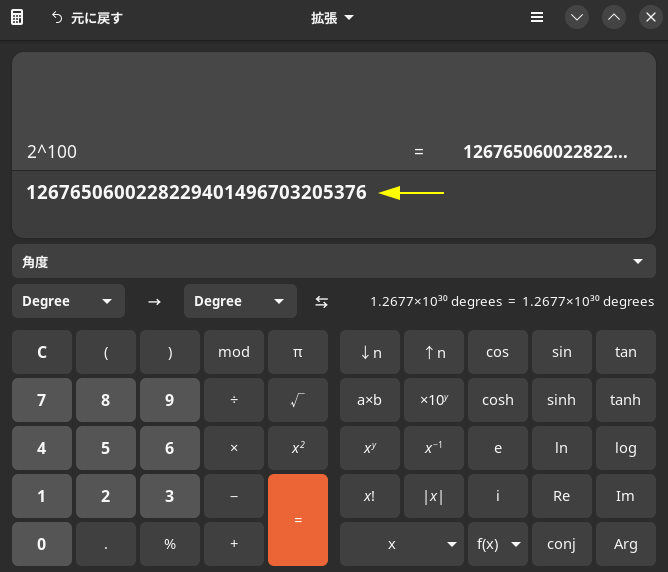
…とてつもなく長い数字ですね。
では、これをExcelで計算してみましょう。
セルに =2^100 と入力してみてください。

結果は… 1.26765E+30 。
「指数表記」になってしまいました。
セルの表示形式を「数値」に変えても…
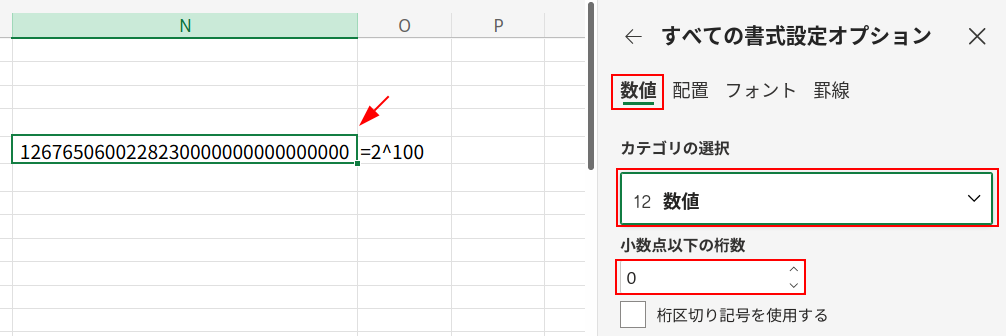
1267650600228230000000000000000
おや? 下の桁が全部「0」になっています。計算が合っていません!
Excelで2^100の計算はできないのでしょうか。
本記事では、無料のWeb版Excelを使用して検証および画像の作成を行っています。Windowsはもちろん、MacやLinuxの方もブラウザさえあれば挑戦できます!
なぜExcelは計算できないのか?
これはExcelのバグではありません。
Excel(というより多くのコンピュータ)が採用している「IEEE 754」という規格の仕様です。
Excelは数値を「倍精度浮動小数点数」という形式で扱っています。
これは、ものすごく大きな数や小さな数を扱える代わりに、有効桁数が「約15桁」までという制限があります。
つまり、16桁目以降の細かい数字は「誤差」として切り捨てられ、0になってしまうのです。

しかし、こんなことでは諦めません。
今回のテーマは、「Excelの制約を工夫で乗り越え、![]() を1の位まで正確に表示する」こと!
を1の位まで正確に表示する」こと!
このパズルを解くことで、データを工夫して扱う「応用力」と、桁上がりを制御する「論理的思考力」が身につきます。
さあ、限界突破の旅に出ましょう!
作戦:巨大な数字は「ブロック」に分けろ!
関数の詳細な仕様については、Microsoft公式のヘルプも参考にしてください。
![]() の桁数は、
の桁数は、=LOG10(2^100) で計算すると約「30.1」となるため、31桁の整数であることが分かります。
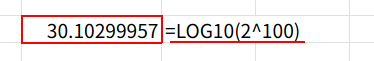
15桁しか扱えないなら、10桁ずつ3つか4つのブロックに分けて計算し、最後に合体させればいいのです!
今回は余裕を持って、10桁×4ブロック(A列~D列)で計算します。
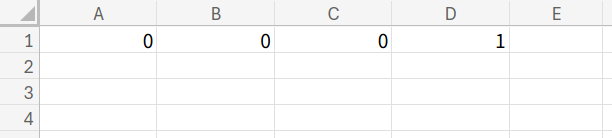
ステップ1:準備
1行目に初期値(![]() )を入力します。
)を入力します。
- A1:
0 - B1:
0 - C1:
0 - D1:
1
ステップ2:筆算のロジックを数式にする
2行目に、前の行を2倍する数式を入れます。
ただし、単に2倍するだけでは「10桁」を超えてしまいます。
そこで、「10桁を超えた分(繰り上がり)」を左の列に渡す処理を行います。
続いて、A2~D2セルに、以下の数式を入力してください。
A2セル(最上位ブロック):=MOD(A1*2+INT((B1*2+INT((C1*2+INT(D1*2/10^10))/10^10))/10^10),10^10)
B2セル(上位ブロック):=MOD(B1*2+INT((C1*2+INT(D1*2/10^10))/10^10),10^10)
C2セル(中位ブロック):=MOD(C1*2+INT(D1*2/10^10),10^10)
D2セル(下位ブロック):=MOD(D1*2,10^10)

数式の解説(D列とC列の例)
D2(下位)のロジック:MOD(D1*2, 10^10)
前の値を2倍します。もし10桁を超えても、MOD(..., 10^10) で下10桁だけを残します。

C2(中位)のロジック:MOD(C1*2 + INT(D1*2/10^10), 10^10)
1. C1*2: 自分の桁を2倍します。
2. INT(D1*2/10^10): 右隣(D列)で2倍した時にあふれた分(繰り上がり)を受け取って足します。

3. MOD(..., 10^10): 足した結果がさらにあふれたら、それは左隣(B列)に任せて、自分は下10桁だけを残します。
これをA列までリレーさせていくわけです!
ステップ3:フィルコピーして完成!
入力したA2:D2を選択し、101行目までガガーッと下にオートフィル(コピー)してください。
1行目が「0乗」なので、101行目が「100乗」の結果になります。
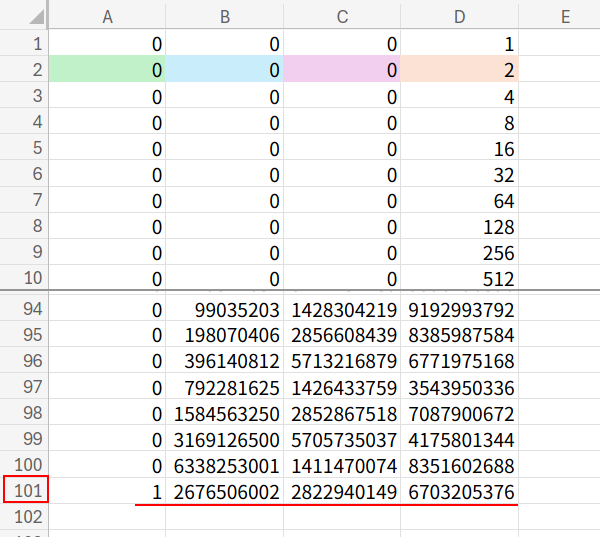
最後に、任意のセルでこれらを連結します。
ただし、単純に & で繋ぐと、途中の(例)「0000000123」が「123」になってしまい桁がズレます。
※今回(2^100)の場合は問題ありませんが、そのようなケースを想定します。
必ず TEXT関数 で10桁のゼロ埋めを行いましょう。
=TEXT(A101,"0")&TEXT(B101,"0000000000")&TEXT(C101,"0000000000")&TEXT(D101,"0000000000")
結果は…
1267650600228229401496703205376
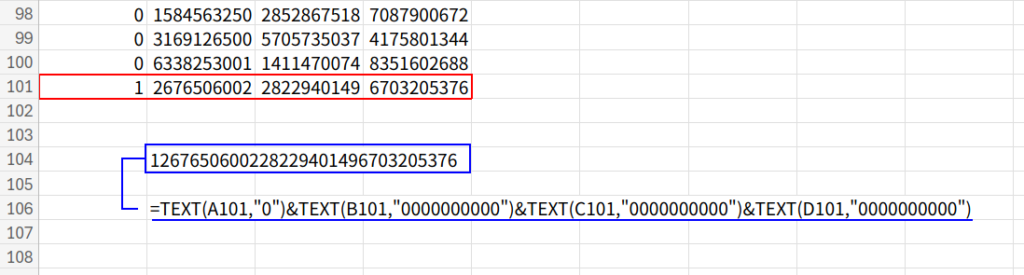
電卓の結果と見比べてみてください。
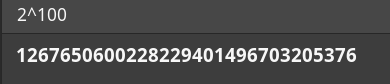
一桁の狂いもなく、完全一致しているはずです!
Excelの15桁の壁を、知恵と工夫で突破しました!
ミッション2:一撃で解く!作業列なしの数式
「フィルコピーが面倒くさい!」
そんな方のために、最新のExcel関数(REDUCE & LAMBDA)を使って、この計算を一発で行う数式を紹介します。
数式
=LET(
初期配列, {0,0,0,1},
ブロック桁数, 10^10,
計算結果, REDUCE(初期配列, SEQUENCE(100), LAMBDA(現在の値,_,
LET(
倍増, 現在の値 * 2,
繰り上がり, INT(倍増 / ブロック桁数),
シフト処理, HSTACK(DROP(繰り上がり, , 1), 0),
MOD(倍増 + シフト処理, ブロック桁数)
)
)),
TEXT(INDEX(計算結果, 1), "0") & CONCAT(TEXT(DROP(計算結果, , 1), "0000000000"))
)
数式の解読
※やっていることは上記とほとんど同じなので画像は省略します!
1. 初期配列: {0, 0, 0, 1} という4つのブロックを用意します。
2. REDUCE & SEQUENCE(100): 初期配列に対して、以下の計算を「100回」繰り返します。
3. LAMBDA内の処理:
倍増: 配列全体を2倍します。繰り上がり: 各ブロックで10桁を超えた分(オーバーフロー)を計算します。シフト処理:HSTACKとDROPを使って、繰り上がり分を「一つ左のブロック」に移動させます。(右端のD列の繰り上がりはC列へ、C列はB列へ…)MOD(...): 倍増した値に、右からの繰り上がりを足し、最後に自分自身が10桁に収まるように余りを取ります。
4. TEXT & CONCAT: 最後に、先ほどと同じようにTEXT関数でゼロ埋めして連結します。
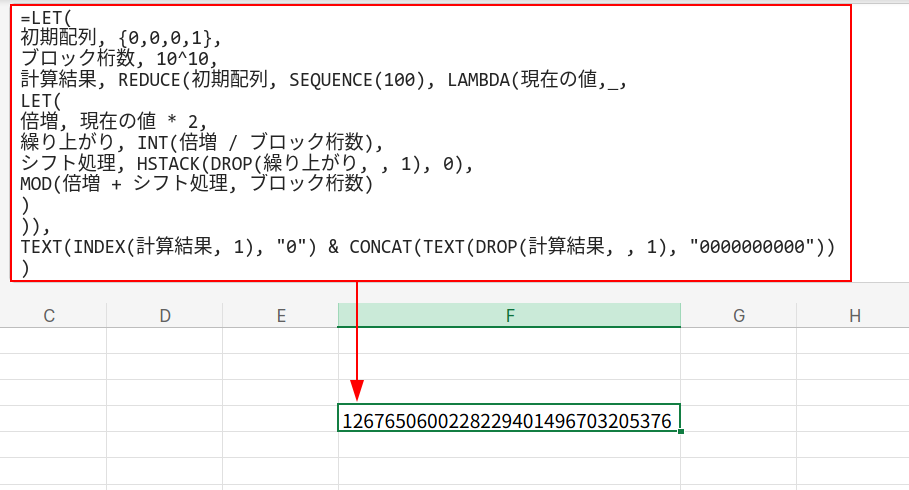
やっていることはフィルコピー版と同じ「筆算の繰り返し」ですが、それをメモリ上だけで完結させているのです。美しいですね!
おまけ:この数字、どう読むの?
せっかくなので、この31桁の数字を日本語で読んでみましょう。
126穣 7650𥝱 6002垓 2822京 9401兆 4967億 320万 5376
(126じょう 7650じょ 6002がい 2822けい…)
「兆」や「京(けい)」までは聞きますが、「垓(がい)」「𥝱(じょ)」「穣(じょう)」なんて単位、見たことありますか?
ちなみに、この ![]() (約
(約 ![]() )という数字に近いものを探すと…
)という数字に近いものを探すと…
- 観測可能な宇宙にある星の数:約
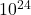 個(まだまだ!)
個(まだまだ!) - 人体の原子の数:約
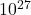 個(惜しい!)
個(惜しい!)
※いずれも諸説あり。
星の数よりも遥かに大きく、体中の原子の数の1000倍。
そんな天文学的な数字を、Excelのセルの中に正確に封じ込めたのです。
まとめ:制限があるからこそ面白い
「Excelは15桁までしか計算できない」
それは事実ですが、諦める理由にはなりません。
仕組みを理解し、ブロックに分けて統治する。
この考え方は、プログラミングや大規模データの処理にも通じる重要なスキルです。
何より、こんな巨大な数字がピッタリ合った時の快感はたまりませんよね!
ぜひ、皆さんのExcelでも ![]() の扉を開いてみてください!
の扉を開いてみてください!
他の、数学系のネタも是非ご覧ください。
Excelで行列計算!連立方程式を一瞬で解く5つの関数テクニック
【Excel】素因数分解を関数だけで実装?LAMBDAと再帰で挑むアルゴリズム



