はじめに：目が…目がぁ！Excelで「錯視」を作って脳を騙そう
みなさん、突然ですが、こんな絵を見たことはありますか？
じーっと見てください。
なんだか、横のラインがグニャグニャと歪んで見えませんか？
「うわっ、本当に曲がってる！」と思った方、安心してください。
あなたの目は正常ですし、モニターが壊れたわけでもありません。
これは、「カフェウォール錯視（Cafe Wall illusion）」、
あるいはその原型となった「ミュンスターバーグ錯視」と呼ばれる視覚効果です。
実際にはすべての線が平行で直線なのに、白と黒のコントラストと、その間にある「グレーの境界線」が脳の処理をバグらせて、傾いているように錯覚させているのです。
さて、ここからが本題です。
「これ、Excelで再現できるんじゃね？」
今回は、この不思議な錯視をExcelシート上で再現するのがミッションです。
もちろん、手作業でセルを塗りつぶしてコピペ…なんて野暮なことはしません。
ここは「Excelで暇つぶし」。数式と条件付き書式だけで美しく描画してみましょう！
本記事では、無料のWeb版Excelを使用して検証を行っています。Windowsはもちろん、MacやLinuxの方もブラウザさえあれば挑戦できます！
これ何の役に立つの？
「そんなことして何になるの？」という声が聞こえてきそうですが、メリットがありそうです。
- 論理的思考力の向上：複雑な模様を「0と1の配列」に分解して考える力がつきます。
- 配列関数の理解：行列を自在に操る、スピル機能の練習に最適です。
- 条件付き書式の応用：数値を可視化するテクニックが身につきます。
- 飲み会のネタ：「俺、Excelで錯視作れるんだぜ」と言えます（ウケるかは保証しません）。
ロジックを解析せよ
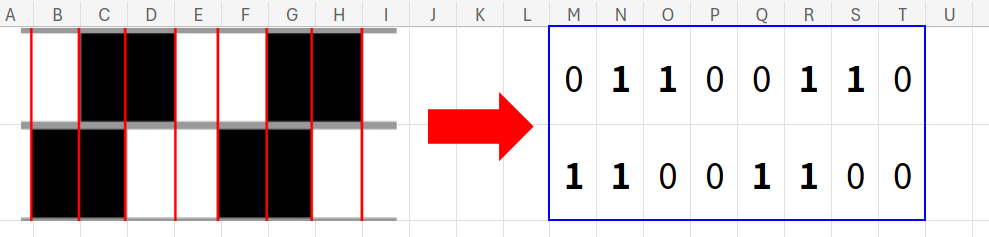
まずは、サンプルの画像をよーく観察して、Excelで再現可能なロジックに落とし込みましょう。
縦に補助線を引いて考えてみると、ある法則が見えてきます。
・1行目は「白、黒、黒、白」の繰り返し（0, 1, 1, 0…）
・2行目は「黒、黒、白、白」の繰り返し（1, 1, 0, 0…）
・3行目以降は、1行目と2行目を交互に繰り返す
つまり、「0011」のようなパターンを作り、それを1行ごとにズラして配置すれば良いわけです。
今回は、見やすさを考慮して「8行 × 20列」の配列を作っていきます。
アプローチ：数式で配列を作る
さあ、ここからがパズルです。
どうやってこの「0と1のまだら模様」を作るか。
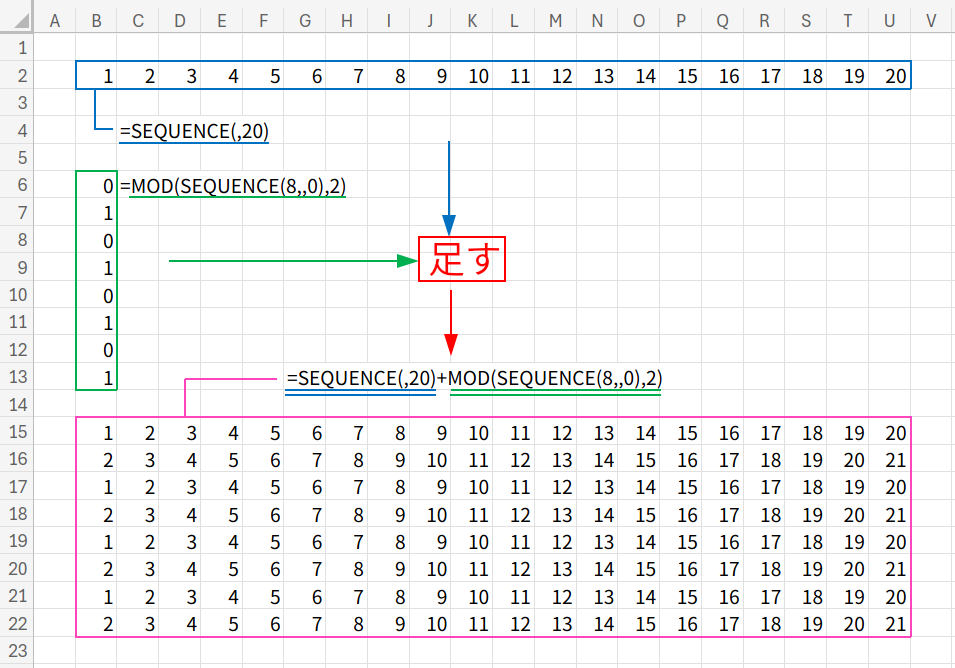
今回は、B2セルを起点に入力します。
A列と1行目は余白として空けておくと、後で罫線が見やすいためです。
マニアックなものも含めて、5つのアプローチを用意しました。
アプローチ1：王道！商と余りを利用
まずは、数学的なアプローチです。これが一番汎用的です。
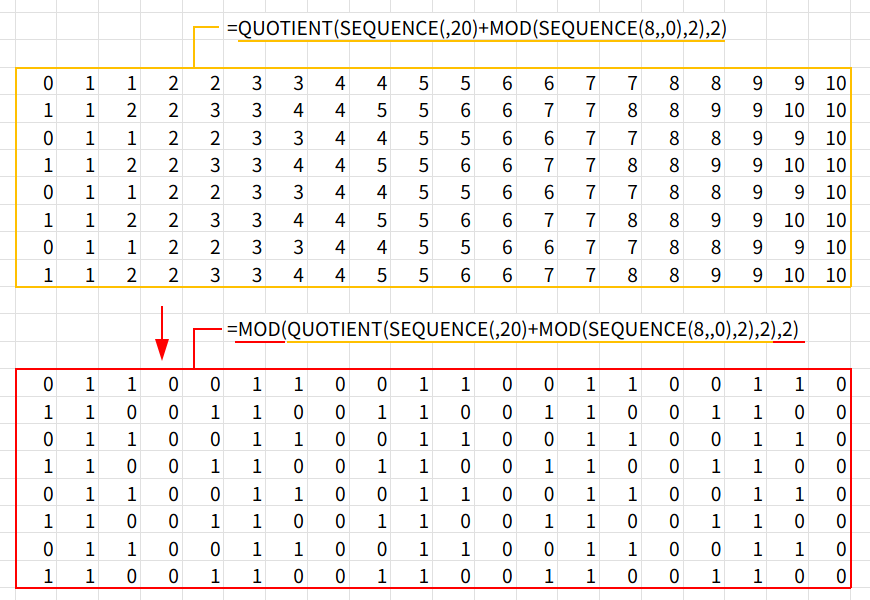
=MOD(QUOTIENT(SEQUENCE(,20)+MOD(SEQUENCE(8,,0),2),2),2)
【数式の解説】
少し複雑に見えますが、順を追って分解すると単純な算数です。
横の連番：SEQUENCE(,20)
横に 1, 2, 3, 4… 20と数字が並びます。
縦のズレ：MOD(SEQUENCE(8,,0),2)
縦に 0, 1, 0, 1… と足し算します。
これにより、奇数行はそのまま、偶数行は「+1」されてスタート地点がズレます。
商で階段を作る：QUOTIENT(..., 2)
2で割った「商（整数部分）」を求めます。
1, 2, 3, 4 → (÷2) → 0, 1, 1, 2… となり、「2つ連続して同じ数字」が並ぶ階段ができます。
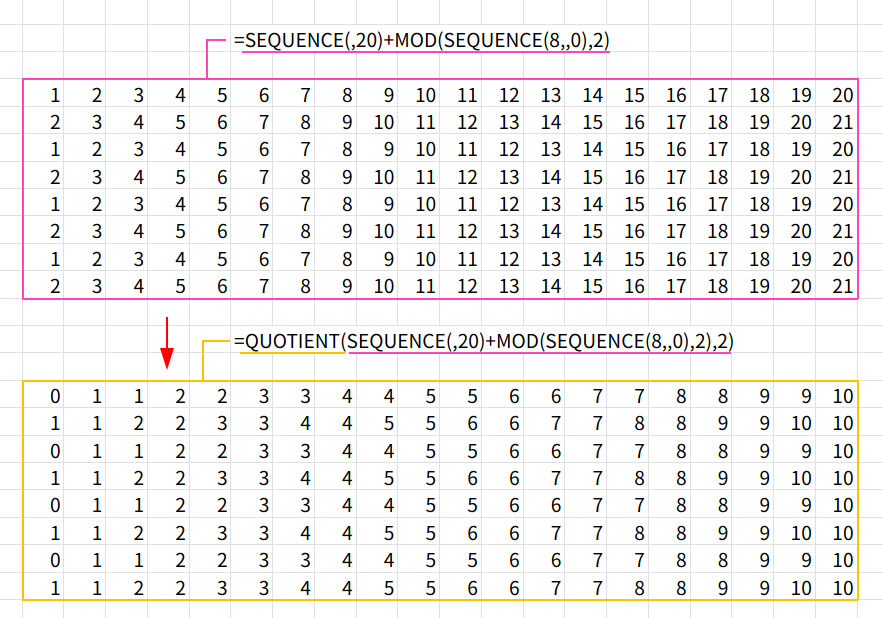
余りで0/1にする：MOD(..., 2)
最後に、2で割った余りを出します。
0, 1, 1, 2, 2, 3… → (MOD 2) → 0, 1, 1, 0, 0, 1…
これで、0と1が2回ずつ繰り返されるパターンの完成です！
※Excel 2019以前の場合（レガシー数式）
SEQUENCE関数が使えない環境では、以下の数式を入力し、Ctrl + Shift + Enter（CSE確定）を押してください。=MOD(QUOTIENT(TRANSPOSE(ROW(INDIRECT("A1:A"&20)))+MOD(ROW(INDIRECT("A1:A"&8))-1,2),2),2)
アプローチ2：MAKEARRAYで現代風に
続いて、最新の関数を使うならこちら。
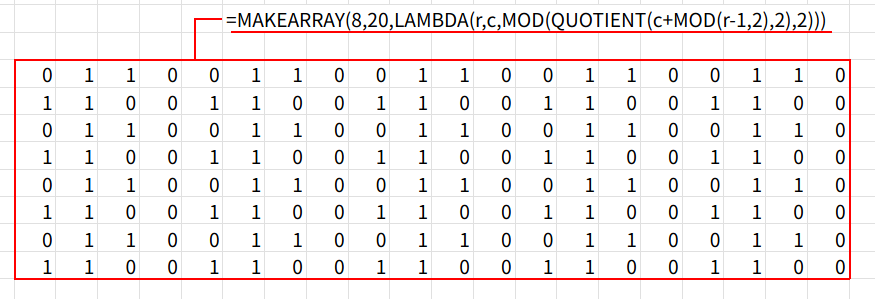
考え方はアプローチ1と同じですが、LAMBDAを使うことで「行(r)」と「列(c)」の関係が記述しやすくなります。
=MAKEARRAY(8,20,LAMBDA(r,c,MOD(QUOTIENT(c+MOD(r-1,2),2),2)))
アプローチ3：無駄にBITANDを使用（マニアック！）
ここからは趣味の世界です。ビット演算を使ってみましょう。
=BITAND(SEQUENCE(,20)+MOD(SEQUENCE(8,,0),2),2)/2
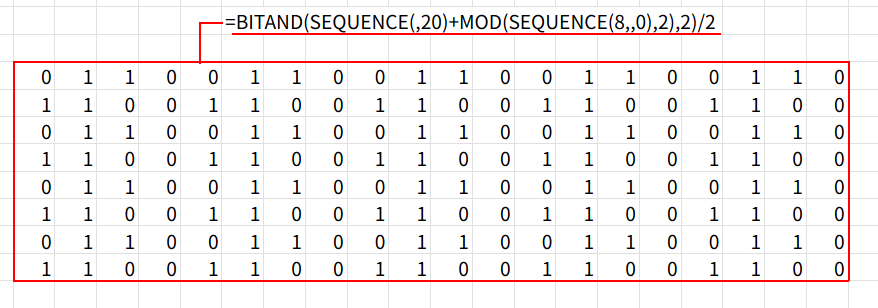
【BITAND関数の解説】
実務ではあまり見かけない BITAND ですが、これは数値を「2進数（ビット）」で比較する関数です。
例えば、今回比較している「2」は、2進数で「10」です。
これは、「下から2桁目のビットが立っているか？」を判定するフィルターとして機能します。
- 数値 0 (2進数 00) → 2桁目は0 → 結果 0
- 数値 1 (2進数 01) → 2桁目は0 → 結果 0
- 数値 2 (2進数 10) → 2桁目は1 → 結果 2
- 数値 3 (2進数 11) → 2桁目は1 → 結果 2
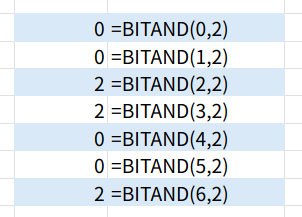
このように、0, 0, 2, 2… という結果が返るので、最後に「/2」で割れば 0, 0, 1, 1… となります。
似た関数に BITOR（ビットごとの論理和）や BITXOR（排他的論理和）があり、フラグ管理やネットワークのサブネットマスク計算などで使われますが、こんな遊び方もできるのです！
アプローチ4：長い文字列を作って分解
「計算なんて面倒だ！」という力技派へ。文字列操作で解決します。
=MID(REPT("0110",10),SEQUENCE(,20)+MOD(SEQUENCE(8,,0),2),1)*1
まず、"0110"という文字列を10回繰り返して超長い文字列を作ります。
そこからMID関数で必要な場所を切り抜いています。
シンプルで分かりやすいですね。
アプローチ5：SIN関数の波を利用
最後は、数学のロマン！三角関数です。
=1*(SIN((SEQUENCE(,20)+MOD(SEQUENCE(8,,0),2)-1.5)*PI()/2)>0)
波がプラスになっている部分だけを「1」として取り出しています。
Excelで波形処理をしている気分になれます。
仕上げ：条件付き書式で「錯視」を発動させる
数式を入力すると、画面には「0」と「1」の数字が並んでいるはずです。
これを、条件付き書式で「白」と「黒」に塗り分けましょう。
手順1：黒く塗る
まず、数式が入っている範囲（B2:U9）を選択します。
「ホーム」タブ →「条件付き書式」→「新しいルール」を選択。
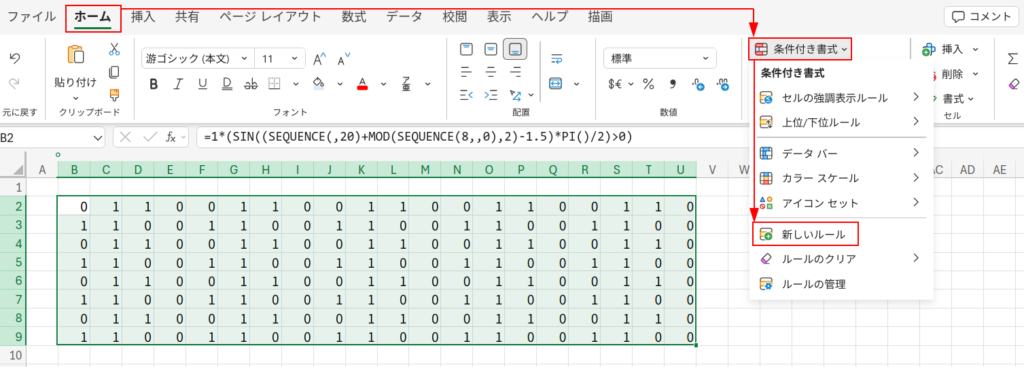
次に、「数式がtureのセルを書式設定する」を選びます。
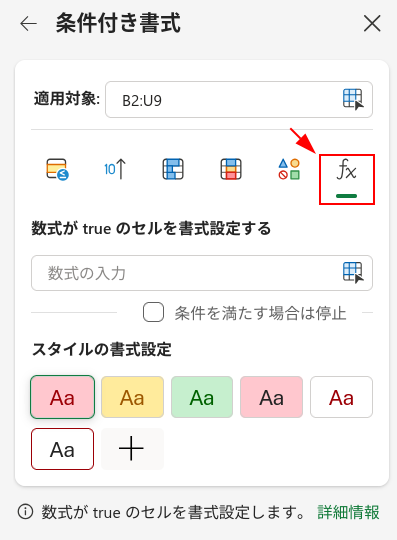
数式に =B2=1 と入力します。
続いて、「書式」ボタンを押し、フォントの色と塗りつぶしの色を両方とも「黒」にします。
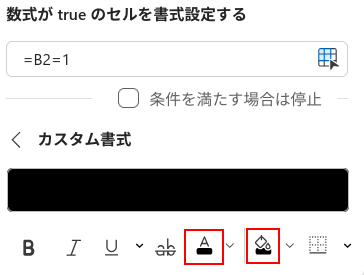
最後に、「完了」を押します。
手順2：白く塗る
- 同じ範囲（B2:U9）を選択したまま、「新しいルール」を追加します。
- 数式に
=B2=0と入力します。 - 「書式」ボタンを押し、フォントの色と塗りつぶしの色を両方とも「白」にします。
- 「完了」を押します。
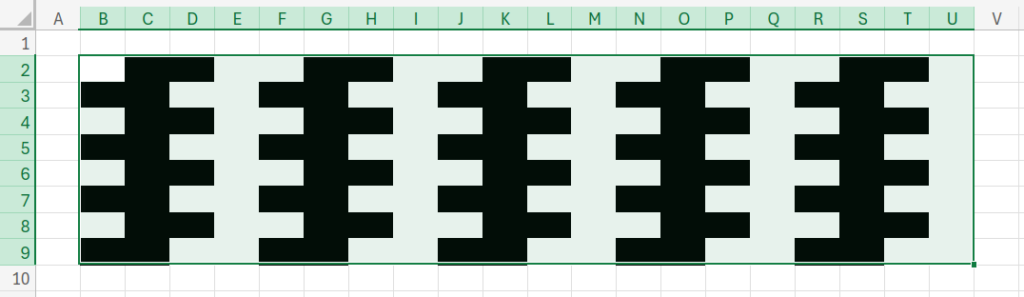
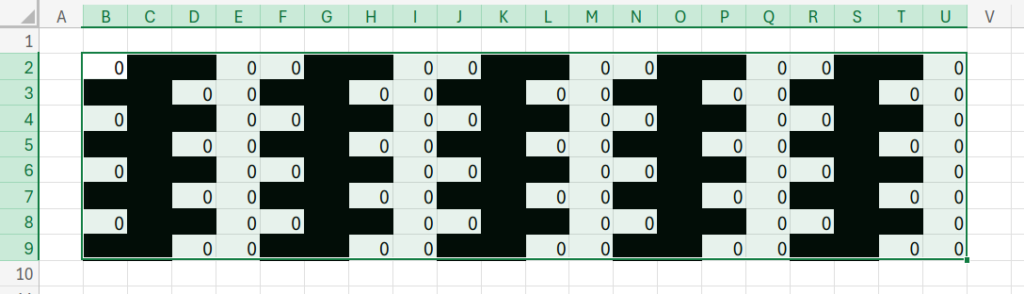
これで、画面上には白と黒の四角形だけが並んだ状態になります。
今度は、列の幅や行の高さを調整して、四角形がなんとなく「正方形」に見えるように調整してください。（Web版Excelの方は目分量でOKです！）
最後の魔法：罫線を引く
さて、今のままだと、ただのチェック柄です。まだ歪んで見えませんよね？
錯視を発動させる最後のトリガー、それが「灰色の罫線」です。
B2:U9の範囲を選択して、Ctrl + 1（セルの書式設定）を開きます。
まず、「罫線」タブを選びます。
次に、線のスタイルで「中くらいの太さ」を選びます。
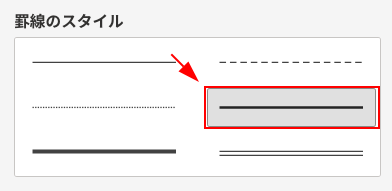
色は、「灰色」（#c8c8c8あたり）を選びます。
最後に、「上」「下」「中（横）」の横方向の線をクリックして適用します。（縦線は引かなくてもOKですが、引いても面白いです）
さあ、シートに戻って画面を見てみてください。
ぐにゃ〜〜〜っ
と、歪んで見えませんか！？
全ての行は真っ直ぐ水平なのに、なぜか交互に傾いているように見えるはずです。
まとめ：自分の目を疑え！
Excelの数式と書式設定だけで、脳を騙すことができました。
今回は灰色の罫線を使いましたが、ぜひ遊んでみてください。
- 罫線を「黒」にしたらどうなる？（たぶん錯視が消えます）
- 罫線を「白」にしたら？
- 罫線を「赤」や「青」にしたら？
- 罫線を極太にしたら？
「どんな条件のときに脳がバグるのか」を探求するのも、また一興です。
それでは、よきExcelライフを！
