この記事は「Excel縛りプレイ」です。 普通に平均を出したい方は、素直に AVERAGE関数 を使ってください(笑)
この記事は、「あえて難しい方法で計算してみたい!」というExcelマニアな方向けのパズル解説記事です。
- 平均といえばAVERAGE関数! でもそれだけじゃない!
- 今回のミッション
- データの準備
- 方法1:基本に忠実! 合計 ÷ 個数 (SUM / ROWS)
- 方法2:行列計算と条件付きカウント (MMULT / COUNTIF)
- 方法3:条件付き合計と最終数値位置 (SUMIF / MATCH)
- 方法4:条件付き合計と条件付きカウント(複数条件版) (SUMIFS / COUNTIFS)
- 方法5:統計関数の合わせ技! (SQRT / SUMSQ / DEVSQ / VAR.P)
- 方法6:対数・指数と文字列操作の狂想曲 (LN / PRODUCT / EXP / TEXTJOIN / LEN / SUBSTITUTE)
- 今回登場した関数
- まとめ
平均といえばAVERAGE関数! でもそれだけじゃない!
「Excelで平均を出すなら、AVERAGE関数でしょ?」
そう思ったあなた、もちろん正解です!
多くの場合、AVERAGE関数が最も手軽で分かりやすい方法です。
でも、今回もちょっと待ってください!
Excelの世界は広大です。
平均を計算する方法は、AVERAGE関数だけではありません。
「え、AVERAGE関数以外でどうやって平均を?」
「しかも、SUBTOTALやAGGREGATEも使わずに?」
そんな、少しひねくれた関数パズルに挑戦してみましょう!
今回の記事では、実務ではまずお目にかからないであろう、マニアックなテクニックも登場します。
それは「AVERAGE系関数、SUBTOTAL、AGGREGATEを使わずに平均を求める」こと!
ここでは、6つの異なるアプローチを紹介します。
目的:様々な関数の使い方や、数式の組み立て方の「引き出し」を増やすこと!
- 行列計算で合計が出せるのは知ってたけど、平均も?
- 統計関数を組み合わせると平均になるの!?
- 対数と指数、文字列操作…?
きっと、そんな驚きと発見があるはずです。
念のため言っておきますが、
実務では素直にAVERAGE関数を使うのが一番安全で効率的です(笑)
でも今回は、あえて関数だけでどこまでできるか、その可能性を探ってみましょう!
この関数パズルを通して、あなたのExcel関数への理解が、さらに一段階レベルアップするかもしれませんよ!
本記事では、Excel 2021を使用して検証および画像の作成を行っています。
今回のミッション
現在の状態とゴール
まず、B1セルからB8セルに8個の数値が入力されています。
(隣のA列には科目名が入っていますが、今回は計算に使いません。)
次に、このB1からB8セルに入力された数値の平均値を、Excelの「関数」だけを使って計算します。
そして、その結果を B9セルからB14セルに、
それぞれ異なる方法で表示させます。
ルール:関数縛り&データ変更禁止!
- 関数のみ: 結果は、各セル(B9~B14)に入力する単一の数式で求めること。VBAは使用禁止。
- 元データ変更禁止: A1:B8 の元のデータは一切変更・加工しない。
- 基本禁止関数: AVERAGE関数系(AVERAGE, AVERAGEA, AVERAGEIF, AVERAGEIFS, TRIMMEAN)、SUBTOTAL関数、AGGREGATE関数は、すべての方法で使用禁止。
これらは簡単に平均を出せてしまうため、今回は封印。 - 追加禁止関数: 方法2以降、使用できる関数にさらに厳しい制限あり。
- Excelバージョン: Excel 2021で利用可能な関数のみを使用。(筆者のExcelが2021のため)
データの準備
まず、新しい空白のExcelシートを用意してください。
次に、計算対象となる数値データをB1セルからB8セルに入力します。その下に数式を入力していきます。(練習なので値は何でも構いません。)
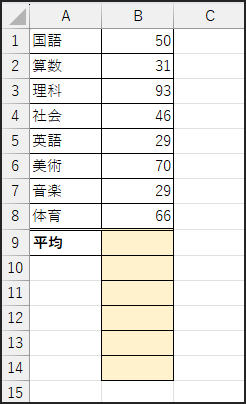
もしくは、下の範囲をコピー&ペーストしましょう。
| 国語 | 50 |
| 算数 | 31 |
| 理科 | 93 |
| 社会 | 46 |
| 英語 | 29 |
| 美術 | 70 |
| 音楽 | 29 |
| 体育 | 66 |
さあ、これで準備はできましたか?
AVERAGE関数の呪縛(?)から解き放たれる、平均値計算の冒険に出発しましょう!
方法1:基本に忠実! 合計 ÷ 個数 (SUM / ROWS)
【使用禁止関数】 AVERAGE系, SUBTOTAL, AGGREGATE
考え方
まずはウォーミングアップです。
平均値の定義といえば、「データの合計 ÷ データの個数」ですよね。
これを最も素直に関数で表現してみましょう。
手順
数式
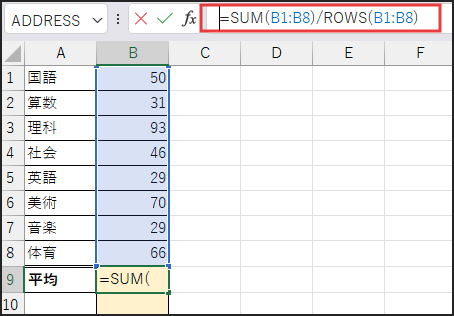
最初に、平均結果を表示したいセル(今回は B9セル)に、以下の数式を入力します。
=SUM(B1:B8)/ROWS(B1:B8)
※個数を求めるのに ROWS(A1:A8) でも ROWS(B1:B8) でも結果は同じです。
解説
数式の概要
この数式は非常にシンプルです。
合計の計算
まず、SUM関数を使って B1からB8 までの数値の合計を計算します。
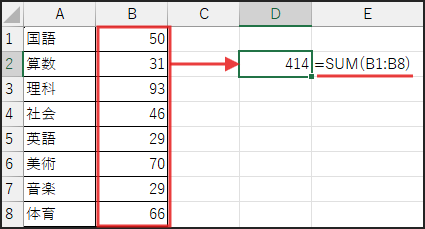
個数の計算
次に、ROWS関数を使って B1からB8 までの行数、つまりデータの個数を取得します。
(今回は8個なので「8」が返ります。)
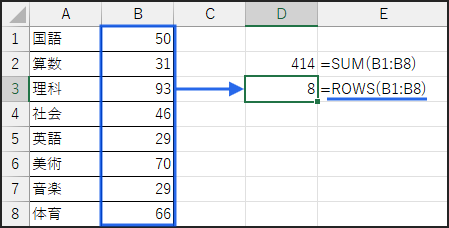
平均値の計算
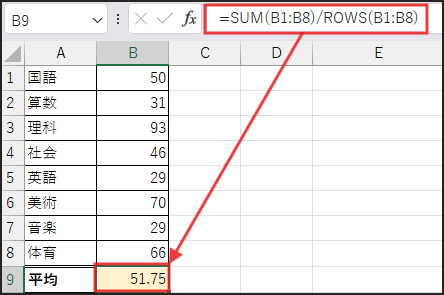
最後に、SUM関数で得られた合計値を、ROWS関数で得られた個数で割り算します。

これで「合計 ÷ 個数」が計算され、平均値が求められます。
メリット&デメリット
- メリット:
- 数式の意味が非常に分かりやすい。
- AVERAGE関数を使わない方法としては最も基本的で理解しやすい。
- デメリット:
- 特になし。ただし、SUM関数やROWS関数が禁止されると使用不可。(次の方法へ続く!)
方法2:行列計算と条件付きカウント (MMULT / COUNTIF)
【使用禁止関数】 AVERAGE系, SUBTOTAL, AGGREGATE, SUM, ROWS
考え方
さて、ここから少しずつ関数に制限がかかります。
今回は「SUM関数」と「ROWS関数」が追加で禁止されました。
合計をSUM関数以外で、個数をROWS関数以外で求める必要があります。
そこで、合計を求める方法として、
前回記事でも登場した行列計算 MMULT を使ってみましょう。
そして、個数は、空白でないセルの数を数える COUNTIF で代用します。
手順
数式入力
次に、B10セルに、以下の数式を入力します。
=MMULT(COLUMN(A1:H1)^0,B1:B8)/COUNTIF(B1:B8,”<>”””)
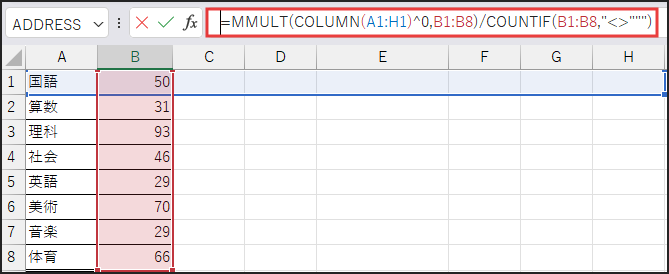
解説
この数式は少し複雑に見えますが、分解していきましょう。
分子の計算(合計値)
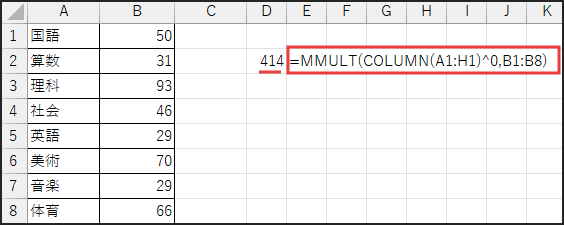
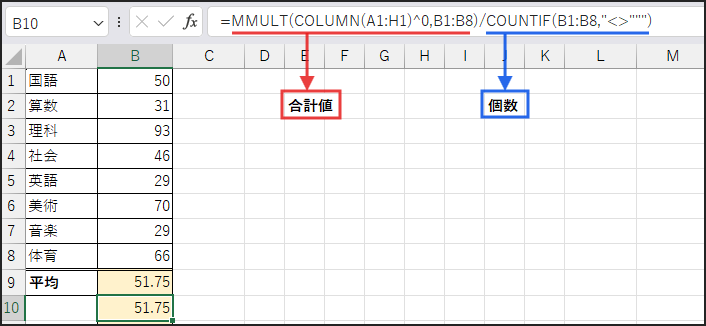
分子部分は MMULT(COLUMN(A1:H1)^0,B1:B8) です。
まず、COLUMN(A1:H1)^0 の部分です。
COLUMN(A1:H1) で {1, 2, …, 8} という列番号の配列を作ります。
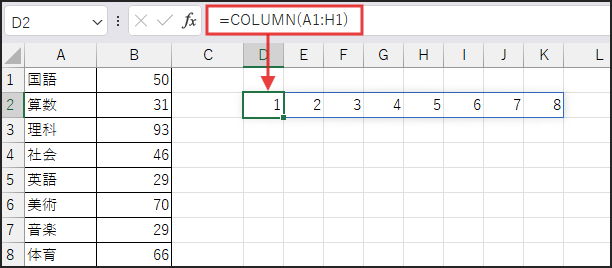
これをそれぞれ ^0 (0乗) することで、
すべての要素が 1 の配列 {1, 1, …, 1} を生成します。
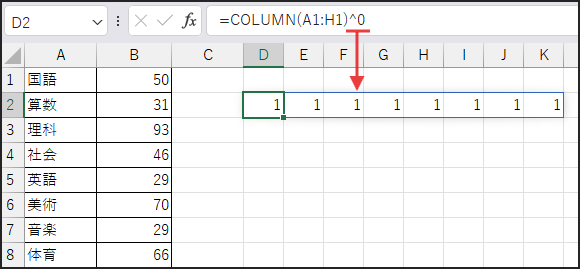
最後に、MMULT(…, B1:B8) で、1行8列の「全要素1の配列」と、
元のデータ範囲 B1:B8 (8行1列) の行列積を計算します。
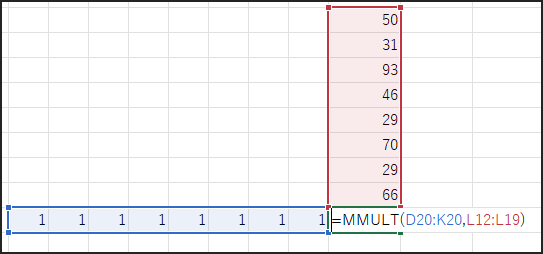
これにより、(1*50 + 1*31 + … + 1*66) という計算が行われ、
結果的に B1:B8 の合計値が求まります。
分母の計算(データ個数)
分母部分は COUNTIF(B1:B8,”<>”””) です。
COUNTIF 関数を使って、範囲 B1:B8 の中で、“<>””” つまり「空白でない」セルの個数を数えます。
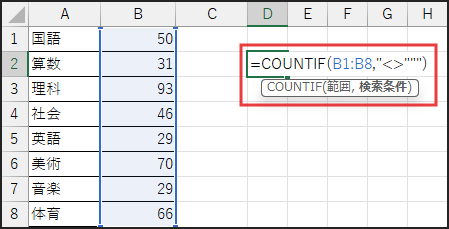
今回は数値データが8個入っているので「8」が返ります。
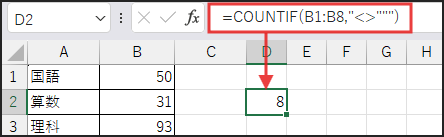
COUNT関数・COUNTA関数 を使ってもOK!
平均値の計算
最後に、分子で計算した合計値を、分母で計算した個数で割り、平均値を求めます。
メリット&デメリット
- メリット:
- SUMやROWSが使えない状況での代替手段となる。
- MMULTによる合計計算テクニックの知識。
- デメリット:
- 行列計算や COLUMN(…)^0 のようなテクニックは直感的でなく、理解が困難。
- COUNTIF(B1:B8,”<>”””) は、数値以外の文字列もカウントする点に注意が必要。(今回は数値のみなのでOK)
方法3:条件付き合計と最終数値位置 (SUMIF / MATCH)
【使用禁止関数】 AVERAGE系, SUBTOTAL, AGGREGATE, SUM, ROWS, COLUMN, MMULT, COUNTIF
考え方
さらに制限が厳しくなります!
行列計算の MMULT と COUNTIF も禁止です。
合計はどうしましょうか? 条件付き合計の SUMIF がまだ使えますね。
個数はどうしましょう?
ここで少しトリッキーな方法ですが、MATCH 関数を使ってみます。
MATCH 関数に非常に大きな数値を指定すると、
範囲内の最後の「数値」の位置を返してくれる特性を利用します。
手順
数式入力
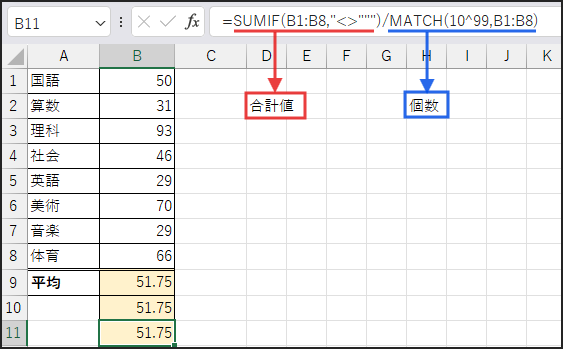
続いて、B11セルに、以下の数式を入力します。
=SUMIF(B1:B8,”<>”””)/MATCH(10^99,B1:B8)
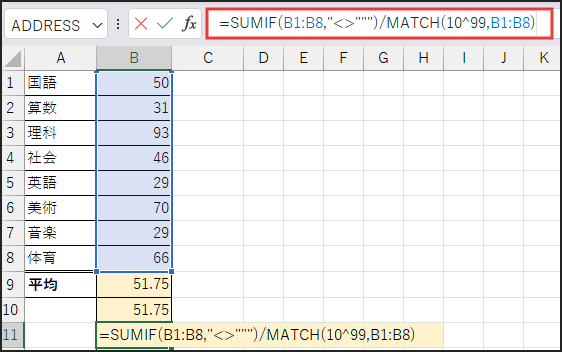
解説
これも一つずつ見ていきましょう。
分子の計算(合計値)
分子は SUMIF(B1:B8,”<>”””) です。
SUMIF 関数は、指定した条件に一致するセルの合計を計算します。
ここでは、範囲 B1:B8 の中で、条件 “<>””” (空白でない) セルの合計を計算します。
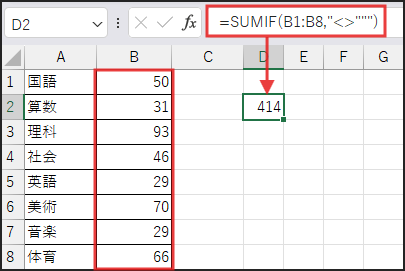
結果的に、範囲内のすべての数値の合計が得られます。
分母の計算(データ個数)
分母は MATCH(10^99,B1:B8) です。
MATCH 関数は、検査値が検査範囲の中で何番目にあるか(相対的な位置)を返します。
ここで 10^99 (非常に大きな数値) を検査値として指定します。
そして、数値が含まれる範囲 B1:B8 を検索します。
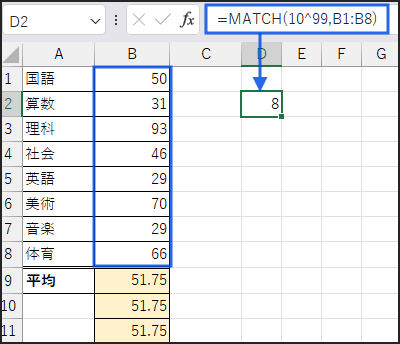
すると、MATCH 関数は「範囲内で、指定した数値以下の最後の数値」の位置を返します。
データがB1からB8まで連続して数値で埋まっている場合、
これは実質的にデータの個数(今回は8)と同じになります。
平均値の計算
最後に、分子の合計値を分母の個数(位置)で割り、平均値を求めます。
メリット&デメリット
- メリット:
- SUMIFとMATCHという、比較的よく使われる関数の組み合わせで実現可能。
- MATCH関数の少し変わった使い方の知識。
- デメリット:
- MATCH関数で個数を求める方法は、データ範囲の途中に空白セルや文字列があると正確な個数を返さない。データが連続している数値であることが前提。
- なぜこれで個数が求まるのか、直感的に分かりにくい。
方法4:条件付き合計と条件付きカウント(複数条件版) (SUMIFS / COUNTIFS)
【使用禁止関数】 AVERAGE系, SUBTOTAL, AGGREGATE, SUM, ROWS, COLUMN, MMULT, COUNTIF, SUMIF, MATCH
考え方
いよいよ主要な計算関数が次々と禁止されてきました。
今回は SUMIF と MATCH が使えなくなりました。
しかし、Excelには複数条件に対応した SUMIFS と COUNTIFS があります。
これらを使って、実質的に「条件なし」と同じように合計と個数を計算してみましょう。
手順
数式入力
さらに、B12セルに、以下の数式を入力します。
=SUMIFS(B1:B8,B1:B8,”<>”””)/COUNTIFS(B1:B8,”<>”””)
解説
これは方法1や方法3と似た発想ですが、使う関数が異なります。
分子の計算(合計値)
分子は SUMIFS(B1:B8,B1:B8,”<>”””) です。
SUMIFS 関数は、複数の条件すべてに一致するセルの合計を計算します。
書式は SUMIFS(合計対象範囲, 条件範囲1, 条件1, [条件範囲2, 条件2], …) となります。
ここでは、合計対象範囲 B1:B8 に対して、条件範囲 B1:B8 の中で “<>””” (空白でない) という条件を設定しています。
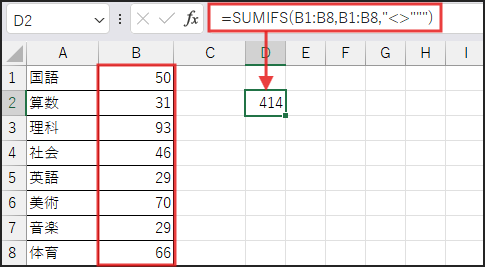
結果として、範囲内の数値すべての合計が得られます。
分母の計算(データ個数)
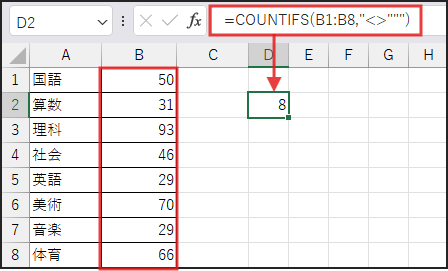
分母は COUNTIFS(B1:B8,”<>”””) です。
COUNTIFS 関数は、複数の条件すべてに一致するセルの個数を数えます。
書式は COUNTIFS(条件範囲1, 条件1, [条件範囲2, 条件2], …) となります。
ここでも、条件範囲 B1:B8 の中で “<>””” (空白でない) という条件に一致するセルの個数を数えます。
結果として、範囲内の数値の個数(今回は8)が得られます。
平均値の計算
最後に、分子の合計値を分母の個数で割り、平均値を求めます。
メリット&デメリット
- メリット:
- SUMIF/COUNTIFが使えない場合の代替となる。
- SUMIFS/COUNTIFSの基本的な使い方(単一条件での利用)の確認。
- デメリット:
- SUMIF/COUNTIFで十分な場合に、あえてSUMIFS/COUNTIFSを使う必要性は低い。
- “<>””” の条件は、数値以外の文字列もカウント対象になる点に注意が必要。(今回はOK)
注意:ここからはマニアックゾーンに突入します!
実用性はほぼゼロですが、関数の可能性を探る旅は続きます…!
方法5:統計関数の合わせ技! (SQRT / SUMSQ / DEVSQ / VAR.P)
【使用禁止関数】 AVERAGE系, SUBTOTAL, AGGREGATE, SUM, ROWS, COLUMN, MMULT, COUNTIF, SUMIF, MATCH, SUMIFS, COUNTIFS
考え方
さあ、さらに禁止関数が増え、SUMIFS と COUNTIFS も使えなくなりました。
合計や個数を直接的に求めるのが難しくなってきましたね…。
ここで視点を変えて、統計関数たちの力を借りましょう!
一見、平均とは関係なさそうな関数(二乗和、偏差平方和、母分散)を組み合わせます。
すると、平均値が計算できてしまうのです!
少しだけ、数学的な知識が必要になります。
手順
数式入力
いよいよ今回のメインディッシュ(?)
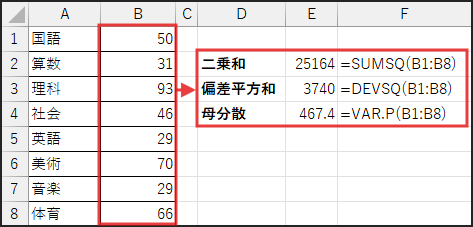
B13セルに、以下の数式を入力します。
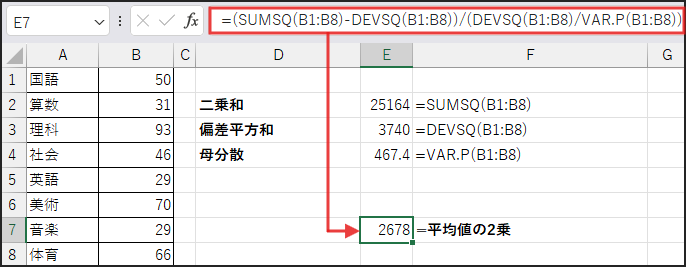
=SQRT((SUMSQ(B1:B8)-DEVSQ(B1:B8))/(DEVSQ(B1:B8)/VAR.P(B1:B8)))

解説
これは…もはや暗号ですね(笑)
頑張って解読しましょう!
数学に関する記事ではないので、簡単にざっくりと解説します!
各統計関数の意味
まず、数式を理解するために、各統計関数の意味と、
平均値 x̄、データ数 n との関係を見ていきます。
- SUMSQ(B1:B8): データ (xi) の二乗和 (∑ xi²) を計算します。
- DEVSQ(B1:B8): データ (xi) の偏差平方和 (∑ (xi – x̄)²) を計算します。
これは、各データと平均値との差を二乗したものの合計です。 - VAR.P(B1:B8): データ (xi) の母分散 (σ² = ∑ (xi – x̄)² / n) を計算します。これは偏差平方和をデータ数で割ったものです。
数式の解析:分母
次に、数式全体を見てみましょう。
SQRT( (SUMSQ(データ) – DEVSQ(データ)) / (DEVSQ(データ) / VAR.P(データ)) )
分母部分に注目します。
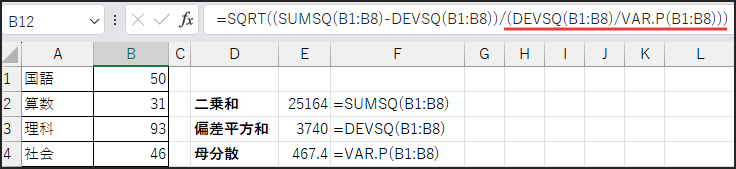
DEVSQ(データ) / VAR.P(データ) = (∑ (xi – x̄)²) / (∑ (xi – x̄)² / n) = n
したがって、分母はデータの個数 n になります!

数式の解析:分子
続いて、分子部分です。
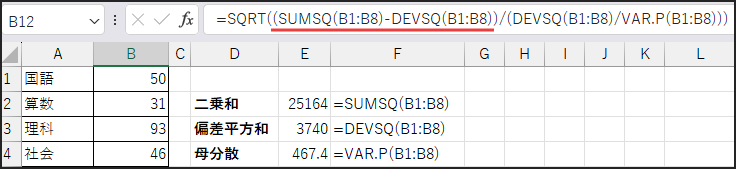
SUMSQ(データ) – DEVSQ(データ) = ∑ xi² – ∑ (xi – x̄)²
ここで、∑ (xi – x̄)² = ∑ xi² – n x̄² という関係式(分散の計算でよく使う式)があります。
これを使うと、
∑ xi² – (∑ xi² – n x̄²) = n x̄²
分子は「個数 n × 平均値 x̄ の2乗」になります!
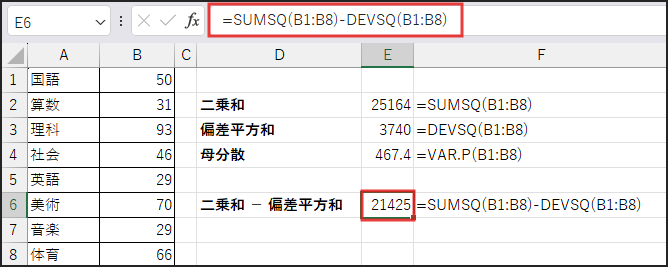
数式の解析:全体
ということは、SQRTの中身全体は、
(n x̄²) / n = x̄²
となり、最後に SQRT (平方根) を取ることで、
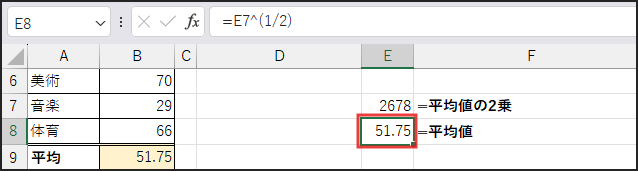
SQRT(x̄²) = x̄
見事に平均値 x̄ が求められる、というわけです!
いやはや、すごい道のりでしたね。
メリット&デメリット
- メリット:
- 統計関数の定義や関係性を深く理解するきっかけになる。(多分!)
- 「こんな方法でも平均が出せるのか!」という驚きがある。
- デメリット:
- 数式の意味がやや難解。数学の知識が必要。
- 実用性は皆無。計算負荷も高そう。
- なぜこれで平均になるのか、説明されてもピンとこない可能性大。
方法6:対数・指数と文字列操作の狂想曲 (LN / PRODUCT / EXP / TEXTJOIN / LEN / SUBSTITUTE)
【使用禁止関数】 AVERAGE系, SUBTOTAL, AGGREGATE, SUM, ROWS, COLUMN, MMULT, COUNTIF, SUMIF, MATCH, SUMIFS, COUNTIFS, SQRT, SUMSQ, DEVSQ, VAR.P
考え方
ついに最終問題!
方法5で活躍した統計関数たち (SQRT, SUMSQ, DEVSQ, VAR.P) も禁止されました。
もう打つ手なしか…?
いいえ、まだExcelには変態的な関数コンボが残されています!
ここでは、数学的な関数の性質(対数と指数)と、
力技の文字列操作を組み合わせます。
そして、平均値をひねり出します!
これが関数パズルの一番の魅力かもしれませんね。
手順
数式入力
最後に、B14セルに、以下の数式を入力します。
=LN(PRODUCT(EXP(B1:B8)))/((LEN(TEXTJOIN(“,”,TRUE,B1:B8))-LEN(SUBSTITUTE(TEXTJOIN(“,”,TRUE,B1:B8),”,”,””)))+1)
※この数式は、Excel 2021以降またはMicrosoft 365が必要です (TEXTJOIN, スピル機能)。
解説
分子と分母に分けて解析しましょう。
もはや無理矢理な数式です。
分子の計算(合計値)
分子は LN(PRODUCT(EXP(B1:B8))) です。
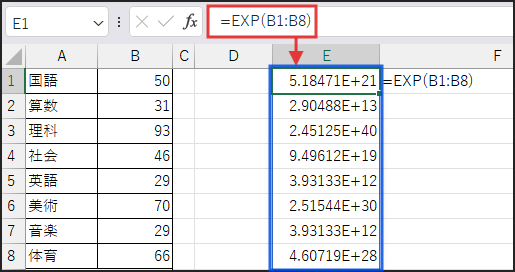
まず、EXP(B1:B8) の部分です。
B1からB8の各数値 xi に対して、EXP 関数で指数 exi を計算します。
Excelのスピル機能により、{eB1, eB2, …, eB8} という配列が生成されます。
次に、PRODUCT(…) で、生成された指数の配列の要素をすべて掛け合わせます (eB1 × eB2 × … × eB8)。
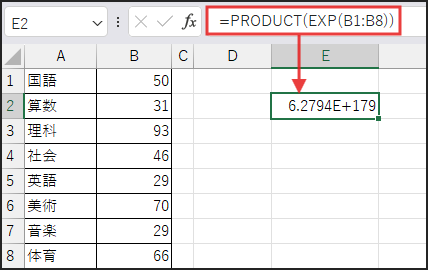
指数の性質から、これは e(B1+B2+…+B8) と等しくなります。
つまり、合計値の指数が得られます。
最後に、LN(…) 関数(自然対数、底がeの対数)を取ります。
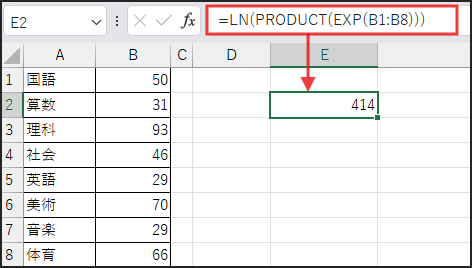
ln(e(B1+B2+…+B8)) は、対数の性質から (B1+B2+…+B8) となり、元の数値の合計値が計算できます!
分母の計算(データ個数)
分母は ((LEN(TEXTJOIN(“,”,TRUE,B1:B8))-LEN(SUBSTITUTE(TEXTJOIN(“,”,TRUE,B1:B8),”,”,””)))+1) です。
まず、TEXTJOIN(“,”,TRUE,B1:B8) で、
範囲 B1:B8 の数値を “,” (カンマ) 区切りで一つの文字列に連結します。
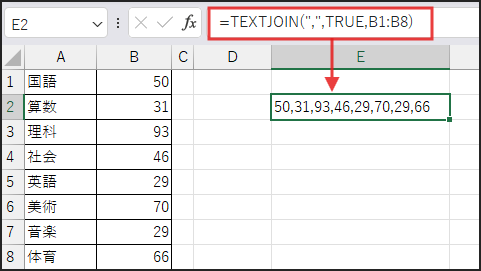
TRUE は空白セルを無視するオプションです。
次に、LEN(…) で、生成された文字列全体の長さを取得します。
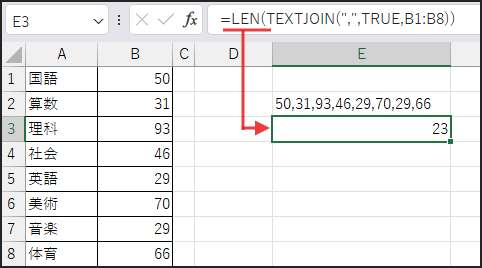
そして、SUBSTITUTE(…,”,”,””) で、連結された文字列から “,” (カンマ) をすべて除去(”” に置換)します。
さらに、LEN(…) で、カンマを除去した文字列の長さを取得します。
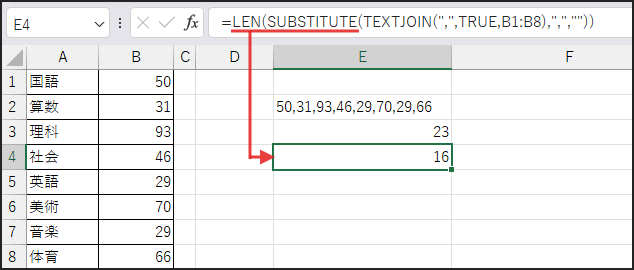
全体の長さからカンマ除去後の長さを引く(LEN(…) – LEN(…))と、
文字列に含まれていたカンマの個数が分かります。

データが8個あれば、カンマは7個になります。
最後に、カンマの個数に 1 を足す((…)+1)ことで、
元のデータの個数(今回は8)が得られます。
(LEN(TEXTJOIN(“,”,TRUE,B1:B8))-LEN(SUBSTITUTE(TEXTJOIN(“,”,TRUE,B1:B8),”,”,””)))+1
平均値の計算
最終的に、分子で得られた合計値を、分母で得られた個数で割り、平均値を求めます。
メリット&デメリット
- メリット:
- 対数・指数関数と文字列操作関数という、
全く異なる分野の関数を組み合わせて目的を達成する発想が面白い。 - 各関数の意外な使い方や連携方法の知識が得られる。
- 「ここまでやるか…」という達成感がある。
- 対数・指数関数と文字列操作関数という、
- デメリット:
- 実用性は完全にゼロ。無駄に関数が多い。
- 数式の意図が極めて分かりにくい。デバッグも困難。
- PRODUCT(EXP(…)) は、元の数値が大きい場合やデータ数が多い場合に、Excelの計算限界を超えてエラーになる(#NUM!)可能性あり。
- TEXTJOIN による文字列連結も、データ量が多いとExcelの文字列長制限に引っかかる可能性あり。
今回登場した関数
今回の挑戦で活躍した関数たちを、簡単に紹介します。
- SUM: セル範囲の合計値を計算。合計の王道。
- ROWS: セル範囲の行数を返す。データの個数カウントに使用可能。
- MMULT: 2つの配列(行列)の積を計算。応用範囲が広いが、少し難しい関数。
- COLUMN: セルの列番号を返す。
- COUNTIF: 指定した条件に一致するセルの個数を数える。
- SUMIF: 指定した条件に一致するセルの合計値を計算。
- MATCH: 検査値が検査範囲内で何番目にあるか(相対的な位置)を返す。検索の基本関数の一つ。
- SUMIFS: 複数の条件すべてに一致するセルの合計値を計算。
- COUNTIFS: 複数の条件すべてに一致するセルの個数を数える。
- SQRT: 数値の正の平方根を返す。
- SUMSQ: 引数の二乗和(各数値を2乗して合計したもの)を返す。
- DEVSQ: データと平均値との差(偏差)の平方和(二乗したものの合計)を返す。
- VAR.P: 母集団全体の分散(データのばらつき具合を示す指標)を計算。
- LN: 数値の自然対数(底がeの対数)を返す。
- PRODUCT: 引数をすべて掛け合わせた結果(積)を返す。
- EXP: 定数eを底とする数値のべき乗 (e数値) を返す。LNの逆関数。
- TEXTJOIN: 指定した区切り文字で、複数の文字列や配列要素を連結。
- LEN: 文字列の長さ(文字数)を返す。
- SUBSTITUTE: 文字列中の指定した文字を、別の文字に置換。
まとめ
今回は、「AVERAGE関数や集計系関数を使わずに平均値を求める」という関数パズルの世界を探求しました。
まず、基本的な「合計÷個数」から始まりました。
次に、行列計算、条件付き計算、難解な統計関数の組み合わせを試しました。
そして最後は対数・指数と文字列操作の合わせ技まで、
実に6つのアプローチを見てきました。
特に後半の方法は、実務で使うことはまず無いでしょう。
迷わず AVERAGE 関数を使うのがベストです。
しかし、普段使わない関数の意外な機能を見つけたり、
難しい数式を読み解いたりするのは、とてもいい勉強になります。
でも、たまにはこんな関数遊びを通して、
Excelの奥深さに触れてみるのも面白いのではないでしょうか。
今回の挑戦が、皆さんのExcelライフに新たな刺激と発見をもたらすきっかけになれば幸いです!