Excel関数で数学パズル!正五角形の外周を求めよう!
なんだか無性に関数をいじり倒したくなる時って、ありませんか?
「複雑な計算式を見ると、ついExcelで再現したくなる…!」…のが筆者です。
そんなExcel好きなあなたに贈る、今回の暇つぶし企画です!
今回のテーマは「半径1の円に内接する正五角形の外周の長さ」を求める数式を、
Excel関数だけで作ってみよう!というものです。
「え、それって数学の問題じゃない?」
そうなんです!
でも、今回はそれをExcelの関数だけで、しかも色々なアプローチで考えてみるのが醍醐味。
普通に計算するだけじゃつまらない!
そこで、あえて関数に縛りを設けたり、
普段使わないような関数を使ってみたり…。
今回の目的は、ズバリ「Excel関数の仕組みや数式の組み立て方への理解を深めること!」です。
「こんな関数も使えるんだ!」「こういう考え方もあるのか!」
こうした発見を通して、
あなたのExcel関数力がレベルアップする…かもしれませんよ?
もちろん、実務でこの計算をすることはないかもしれません(笑)
ですが、色々な方法を知っておくことで、
いざという時の応用力が身につくはずです。
さあ、まずは空白のExcelシートを用意して、
関数と数学の暇つぶしの旅に出かけましょう!
今回のミッション
本記事では、Excel 2021を使用して検証および数式の作成を行っています。
ゴール
Excelの関数だけを使って、「半径1の円に内接する正五角形の外周」を求める数式を作り上げること。
ルール:関数縛りでどこまでできる!?
- ルール1:使用するのはExcelの「関数」のみ!VBA(マクロ)は使いません。
- ルール2:方法が進むにつれて、使える関数に制限を加えていきます。どこまでできるか挑戦してみましょう!
- ルール3:筆者の環境に合わせ、Excel 2021で利用可能な関数を使用します。
データの準備
空白のExcelシート
今回は特別なデータは不要です。計算用のセルがあればOK!
準備はいいですか?
それでは、頭の体操、スタートです!
方法1:基本!三角関数 SIN で求める
使用禁止関数:なし
考えかた
まずは王道から!
図形の問題といえば、やはり三角関数ですよね。
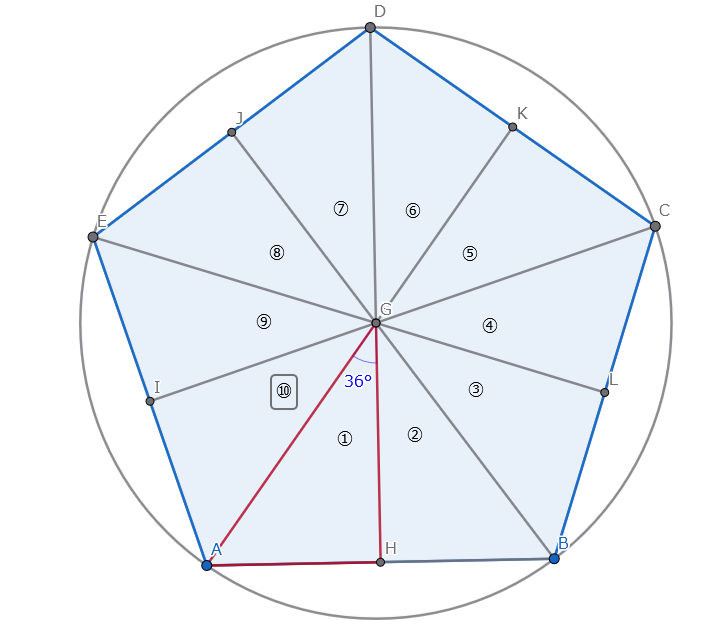
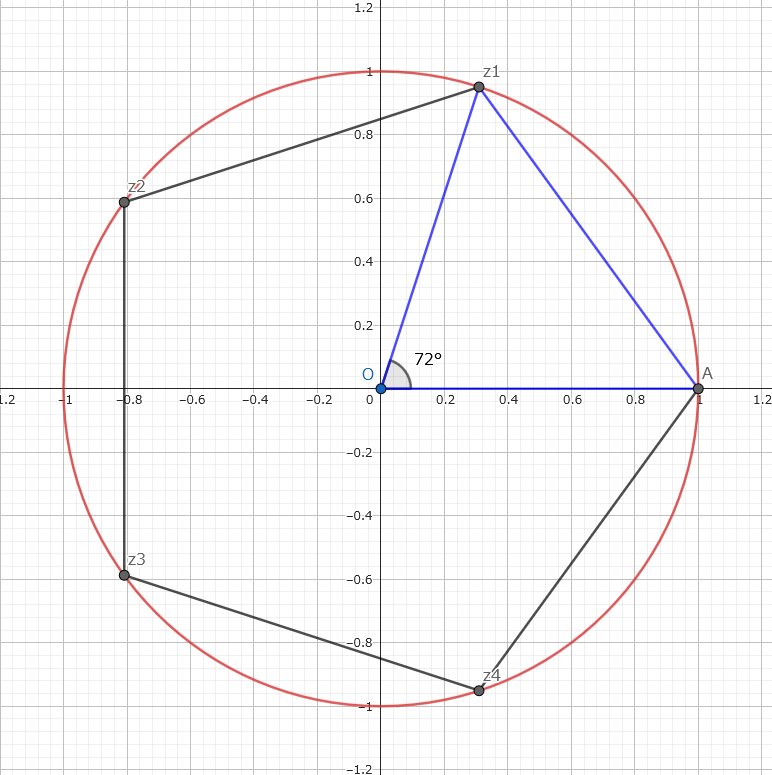
はじめに、半径1の円に内接する正五角形を思い浮かべてみましょう。
次に、円の中心から各頂点に線を引くと、
5つの合同な二等辺三角形ができます。
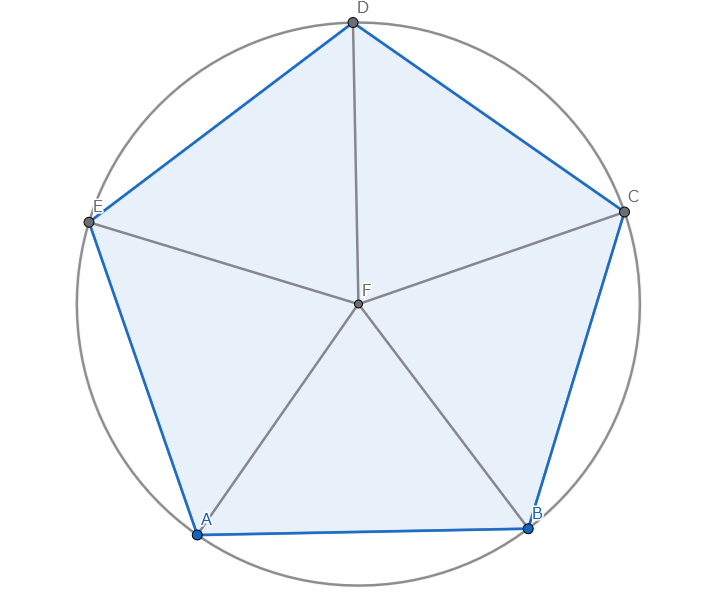
ここで、円の中心角は360度なので、
二等辺三角形の頂角(円の中心部分の角度)は 360度 ÷ 5 = 72度 です。
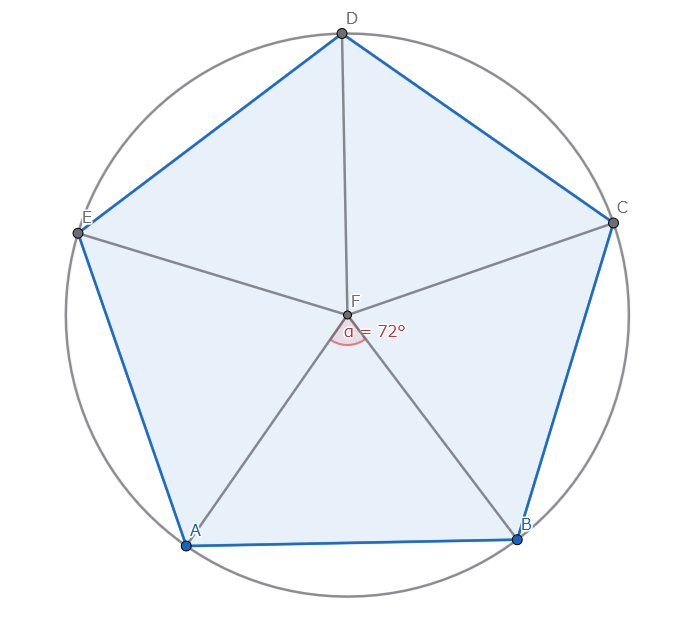
続いて、この二等辺三角形の頂角から底辺に垂線を下ろします。
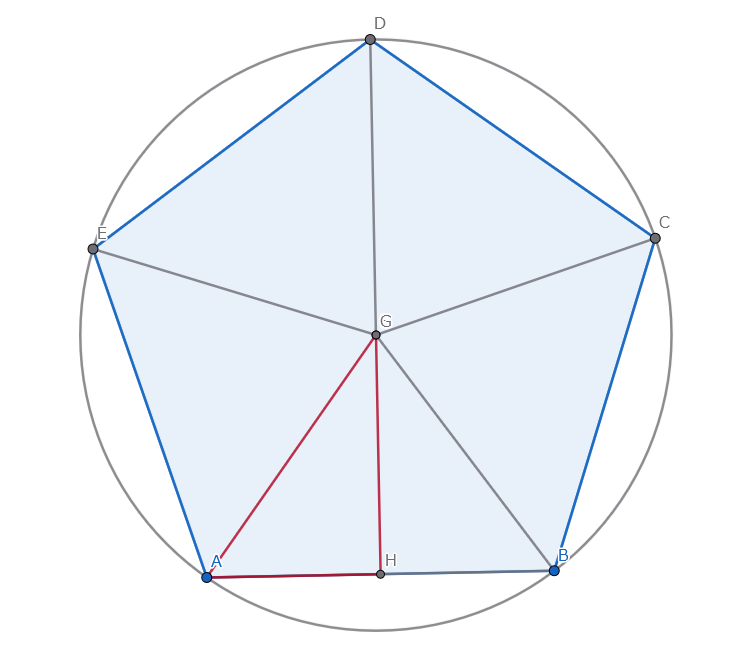
すると、直角三角形が2つできますね。
この直角三角形の、円の中心に対する角度は 72度 ÷ 2 = 36度 になります。
この直角三角形で考えると、斜辺の長さは円の半径なので「1」です。
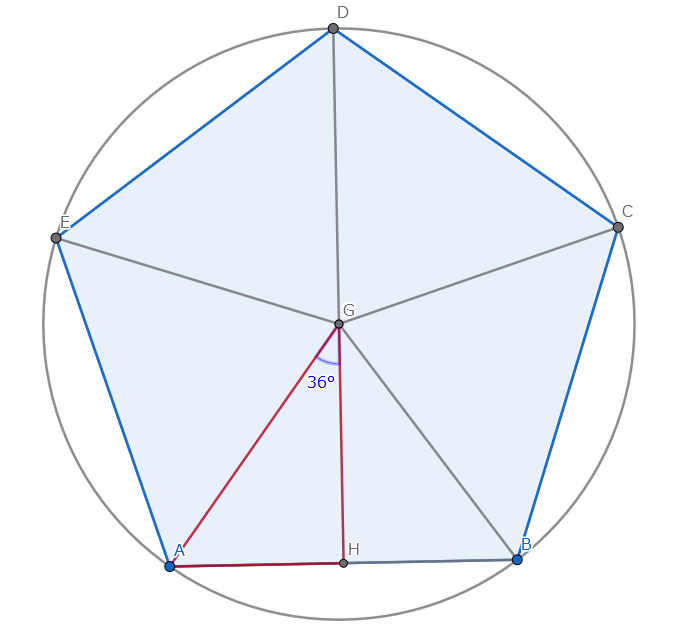
そして、求めたい正五角形の一辺の長さの「半分」は、1 * SIN(36度) で計算できます。
つまり、正五角形の一辺の長さは 2 * SIN(36度) となります。
最後に、外周の長さは、これを5倍すればOKです!
計算式としては、L = 5 * (2 * SIN(36度)) = 10 * SIN(36度) となります。
これをExcelの関数で素直に表現してみましょう!
手順
数式入力
適当なセル (例: A1セル) に以下の数式を入力します。
=10*SIN(RADIANS(36))
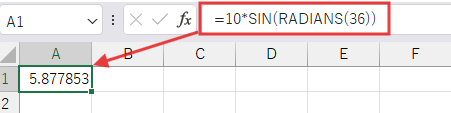
解説
この数式のポイントを見ていきましょう。
SIN関数
SIN(角度) は、サイン(正弦)を計算する関数です。
ただし、
Excelの三角関数は角度を「ラジアン」で指定する必要があります。
RADIANS関数
RADIANS(度数) は、度数法で表された角度(今回は36度)をラジアンに変換する関数です。
円周率PI ラジアン = 180度 の関係を使っています。
全体の計算
10 * … の部分は、最後に10を掛けて、外周の長さを計算しています。
これは、考えた数式 L = 10 * SIN(36度) をそのままExcelで書いた形ですね!
動作確認
入力したセルに 5.877852523… と表示されれば成功です!
これが半径1の円に内接する正五角形の外周の長さです。
方法2:COS と TAN で切り抜ける
使用禁止関数:SIN , RADIANS
考えかた
さて、ここからが暇つぶしの本番!
もし「SIN関数とRADIANS関数、使っちゃダメ!」と言われたらどうしましょう?
でも大丈夫です!
三角関数の世界には、便利な関係式があります。
例えば、TAN(θ) = SIN(θ) / COS(θ) という関係がありましたよね?
これを変形すると SIN(θ) = COS(θ) * TAN(θ) となります。
これを使えば、SIN関数の代わりにCOS関数とTAN関数で表現できそうです!
さらに、角度の単位変換も、RADIANS関数が使えないなら、
円周率PIを使って自力で計算しましょう。
36度をラジアンにするには、36 * 円周率PI / 180 を計算すればOKです。
Excelでは PI() 関数で円周率PIを得られます。
つまり、L = 10 * SIN(36度) = 10 * COS(36度) * TAN(36度) を計算します。
もちろん、角度はラジアンに変換して計算します!
やっていることは、方法1と同じなので画像は省略します。
手順
数式入力
別のセル (例: A2セル) に以下の数式を入力します。
=10*COS(36*PI()/180)*TAN(36*PI()/180)
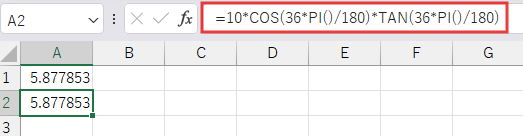
解説
この数式も分解して見てみましょう。
COS関数とTAN関数
COS(角度) はコサイン(余弦)を、
TAN(角度) はタンジェント(正接)を計算します。
PI関数
PI() は、円周率PI (約 3.14159…) を返します。
角度の変換
36*PI()/180 の部分で、36度をラジアンに変換しています。
これは RADIANS(36) と同じ計算結果になります。
全体の計算
COS(…) * TAN(…) により、SIN(36度) と同じ値を計算しています。
そして、10 * … で最後に10を掛けて外周を求めます。
縛りがあっても、別の関数で代替できましたね!
動作確認
入力したセルに、方法1と全く同じ 5.877852523… が表示されれば成功です!
方法3:まさかの三角関数全滅!? 複素数の力でゴリ押し!
使用禁止関数:三角関数系全て, RADIANS
考えかた
さあ、さらに難易度アップ!
「SINもCOSもTANも、三角関数は一切禁止!」
「RADIANSもダメ!」
となったら…?
普通ならお手上げかもしれません。
しかし! Excelにはまだ秘密兵器があります。
複素数関数!
「え、Excelで複素数?」
そうなんです、扱えるんです。
複素数平面でのアプローチ
まず、考え方をガラッと変えます。
複素数平面(実軸と虚軸で表される平面)で、
原点を中心とする半径1の円を考えます。
この円周上の点は、角度 θ を使って e^(i*θ) = COS(θ) + i*SIN(θ) (オイラーの公式)という複素数で表現できます。
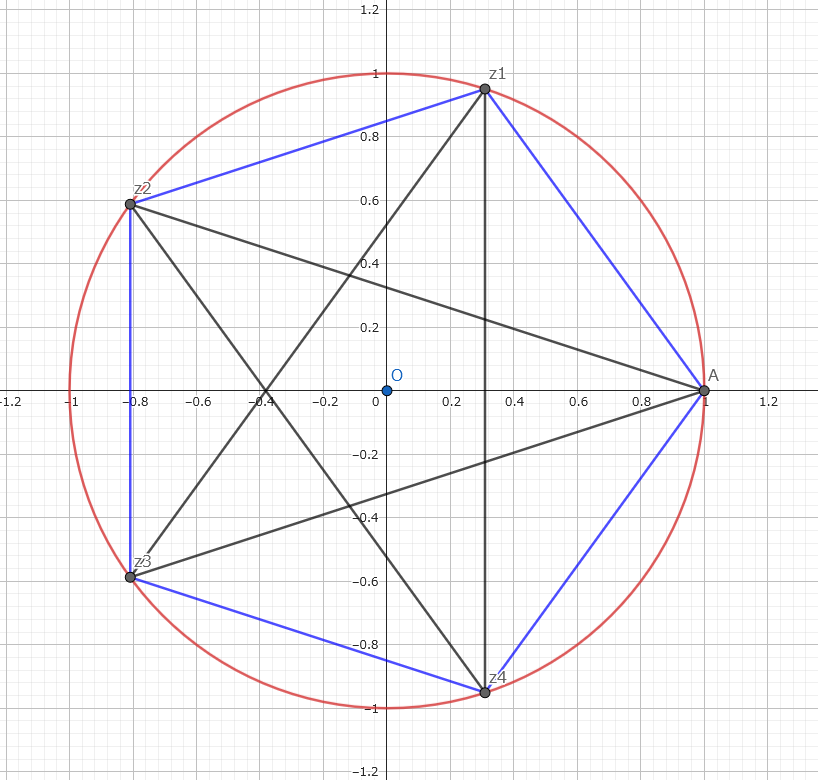
次に、正五角形の頂点は、この円周上に等間隔で並んでいます。
一つの頂点を実軸上の「1」としましょう。
すると、隣の頂点は角度 360度 / 5 = 72度 = 2*円周率PI/5 ラジアンだけ回転した点になります。
これは、複素数では eのi*(2*円周率PI/5)乗 で表せます。
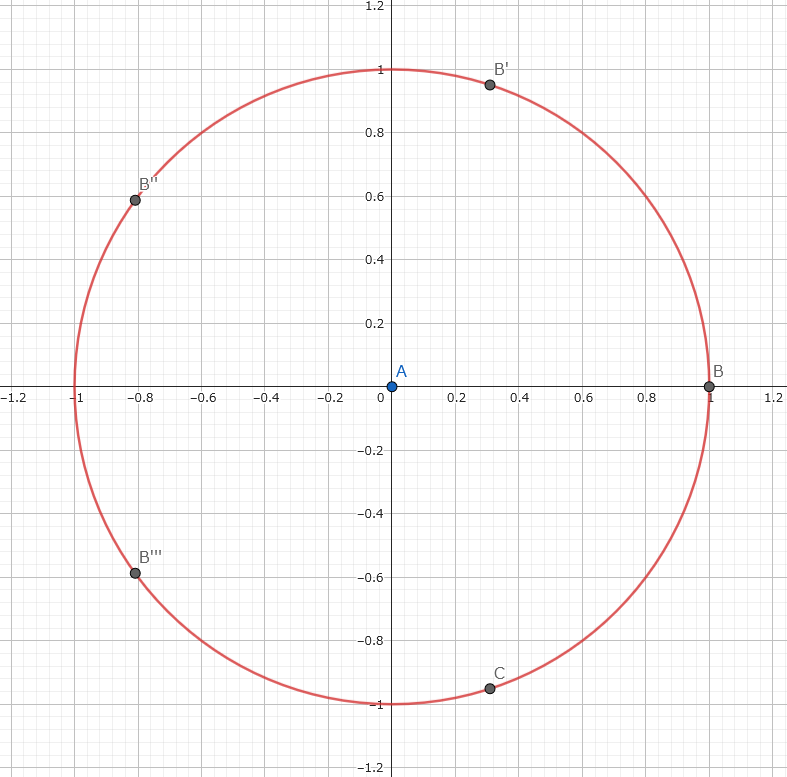
距離の計算
正五角形の一辺の長さは、この2つの頂点「1」と「eのi*(2*円周率PI/5)乗」の間の距離です。
複素数平面上での2点 z1, z2 の距離は、絶対値 |z1 – z2| で計算できます。
今回は、絶対値 |eのi*(2*円周率PI/5)乗 – 1| が一辺の長さになります。
最後に、外周は、この長さを5倍すればOK!
数式で表すと、L = 5 * 絶対値 |eのi*(2*円周率PI/5)乗 – 1|
これをExcelの複素数関数で組み立ててみましょう!
手順
数式入力
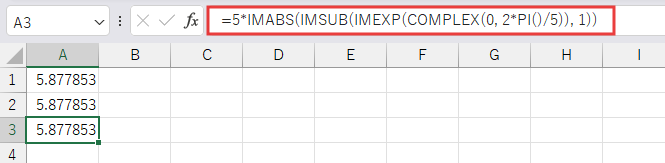
さらに別のセル (例: A3セル) に以下の数式を入力します。
=5*IMABS(IMSUB(IMEXP(COMPLEX(0, 2*PI()/5)), 1))
解説
なんだかすごい見た目の数式ですが、これも分解してみましょう。
角度の計算 (ラジアン)
2*PI()/5 の部分で、
角度 72度 をラジアンで表した値 (2*円周率PI/5) を計算しています。
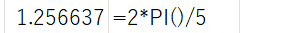
COMPLEX関数
COMPLEX(0, 2*PI()/5) は、
実部が 0、虚部が (2*円周率PI/5) の複素数、つまり i*(2*円周率PI/5) を作ります。

IMEXP関数
IMEXP(複素数) は、eの複素数乗 (ネイピア数eのべき乗) を計算します。

ここでは IMEXP(COMPLEX(…)) で、
eのi*(2*円周率PI/5)乗 を計算しています。
IMSUB関数
IMSUB(複素数1, 複素数2) は、複素数の引き算 (複素数1 – 複素数2) を行います。

ここでは、IMSUB(IMEXP(…), 1) で、(eのi*(2*円周率PI/5)乗) – 1 を計算しています。
数値の1は自動的に複素数 1+0i として扱われます
IMABS関数
IMABS(複素数) は、複素数の絶対値 |複素数| を計算します。
ここでは |(eのi*(2*円周率PI/5)乗) – 1| を計算し、これが正五角形の一辺の長さになります。

全体の計算
5 * … で、最後に5倍して外周を求めます。
これで、三角関数を使わずに、複素数だけで計算できてしまいました!
まさに力技ですね!(やっている内容は高校数学レベル…)
動作確認
入力したセルに、またしても同じ 5.877852523… が表示されたら、
あなたは複素数マスターです!
方法4:関数を使わなくても出来る!(黄金比アプローチ)
考えかた
数学の知識を活用
あれ?
よくよく考えてみると、関数を駆使しなくても、
数学の知識を使えば「値」そのものを計算できますよね?
正五角形といえば、「黄金比」と深い関わりがあります。
そして、半径1の円に内接する正五角形の一辺の長さは、2 * SIN(36度) です。
SIN(36度)の具体的な値
この SIN(36度) の値は、実は SQRT(10-2*SQRT(5))/4 であることが知られています。
証明はちょっと大変なので今回は割愛!興味があれば調べてみてください!
ということは、外周 L = 10 * SIN(36度) は、
L = 10 * (SQRT(10-2*SQRT(5)) / 4) と書けるわけです。
これをExcelで計算してみましょう。
平方根は SQRT 関数でもいいですが、べき乗演算子 ^0.5 でも計算できます。
手順
数式入力
最後のセル (例: A4セル) に以下の数式を入力します。
=10*((10-2*5^0.5)^0.5)/4
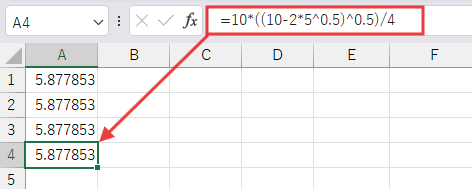
解説
この数式の各部分を見ていきます。
平方根の計算 (SQRT(5))
5^0.5 の部分は、5の0.5乗、
つまり SQRT(5) を計算しています。
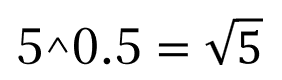
括弧内の計算
10-2*5^0.5 で、10 – 2 * SQRT(5) を計算しています。
全体の平方根
( … )^0.5 で、上記の結果 (10 – 2 * SQRT(5)) の0.5乗、
つまり SQRT(10 – 2 * SQRT(5)) を計算しています。
最終計算
10 * … / 4 で、最後に 10 を掛けて 4 で割り、
外周 L = 10 * (SQRT(10-2*SQRT(5)) / 4) を計算しています。
これはもう、Excel関数というよりは、
数学の公式をそのまま打ち込んだ感じですね!
関数縛りのルールからは少し外れますが、
こんなアプローチもあるということで。
動作確認
もちろん、このセルにも 5.877852523… が表示されるはずです!
参考:今回登場したExcel関数たち
関数リスト
今回の暇つぶしで活躍(?)した関数たちを軽くご紹介します。
- SIN(数値): 数値 (ラジアン) のサインを返します。
- COS(数値): 数値 (ラジアン) のコサインを返します。
- TAN(数値): 数値 (ラジアン) のタンジェントを返します。
- RADIANS(角度): 度数で表された角度をラジアンに変換します。
- PI(): 円周率PI (約 3.14159…) を返します。引数不要!
- COMPLEX(実部, 虚部, [接尾辞]): 実部と虚部から複素数を作成します (例: COMPLEX(1, 2) は 1+2i)。
- IMEXP(複素数): 複素数を指数とする e (ネイピア数) のべき乗 (eの複素数乗) を計算します。
- IMSUB(複素数1, 複素数2): 2つの複素数の差 (複素数1 – 複素数2) を計算します。
- IMABS(複素数): 複素数の絶対値 (原点からの距離) を計算します。
- SQRT(数値): (今回は使いませんでしたが紹介) 数値の正の平方根を返します。数値^0.5 と同じです。
(関数ではありませんが…)
- ^(べき乗演算子): 数値 ^ 指数 でべき乗を計算します (POWER関数と同じ)。
^0.5 で平方根を計算できます。
普段使わない関数も、使ってみると面白い発見がありますね!
まとめ
さて、「半径1の円に内接する正五角形の外周」を求めるExcel関数の暇つぶし、
楽しんでいただけたでしょうか。
まず、三角関数でスマートに解く方法から始めました。
次に、関数縛りで別のアプローチを探る方法も試しました。
そして、複素数を使う方法、さらに数学の知識で直接値を計算する方法までありました。
結果として、色々な角度から同じ答え 5.877852523… にたどり着きました。
正直、方法3の複素数関数は、実務で使う場面はほぼ無いでしょう(笑)
実は、複素数を使えば、Excelのセルが実質“2つの変数”を持つような使い方ができます!
でも、こうやって「あえて違う方法でやってみる」「制限の中で工夫してみる」という思考実験は、Excel関数の本質的な理解につながります。
また、数式を柔軟に組み立てる力を養うのにも役立つはずです。
「この計算はこの関数」と決め打ちするだけでなく、
色々な引き出しを持っておくと、
きっとあなたのExcelスキルはもっと豊かになります!
たまにはこんな「関数パズル」で頭の体操をするのも、楽しいものですね。
今回の暇つぶしが、皆さんのExcelライフのちょっとした刺激になれば幸いです!