Excelで遊んでいる皆さん、こんにちは!
今回も、Excelの新しい「遊び方」を発見してみませんか?
皆さんは、Excelのセルをじっと眺めていると、何かに見えてきたりしませんか?
あのマス目状のセル、実は、まるで碁盤の目のように整然と並んだ「町」のようにも見えてくるんです。

今回の暇つぶしは、まずExcelのセルを「町」に見立てて、マップを作ってみるところから始まります。
そして、そのマップの上で、ある場所からある場所までの「距離」を計算して遊んでみましょう!
単に距離を測るだけでなく、実はここにもExcelの奥深い関数が隠されています。
今回は、マンハッタン距離とユークリッド距離を計算してみよう!
それぞれの計算にどんなExcel関数が使えるのかを探求していきましょう。
遊びながら、いつの間にか関数に詳しくなっちゃう!
そんな楽しい時間を過ごしましょう!
今回のミッション
Excelのセル番地を住所に見立てれば、Excelのシート全体が大きな「町」になります。
そして、それぞれのセルがその町の中の「場所」を表すわけです。
今回は、このExcelという町を舞台に、ちょっとしたマップを作ります。
遊びながら、ある地点から別の地点までの「距離」を計算する方法を学んでいきます。
暇つぶしから始まる関数学習
「距離の計算?何か難しそう…」
と思う方もいるかもしれません。
でも、大丈夫!
今回は難しい数学の話ではなく、「Excelで遊ぶ」ことが目的です。
遊びの中から自然と生まれる「これってどうやるんだろう?」という疑問。
そして、「もっと良い方法はないかな?」という疑問。
その疑問を解決する過程で、Excelの便利な関数に触れることができるんです。
今回の遊びを通して、普段はあまり使わないかもしれない関数を楽しく学んでいきましょう。
こうした関数は、いざというときにきっと役立ちます。
マンハッタン距離とユークリッド距離という2種類の距離を計算してみよう!
町の中である場所から別の場所へ移動するとき、距離の測り方にはいくつかの種類があります。
今回はその中でも代表的な、マンハッタン距離とユークリッド距離という2種類の距離の考え方を学びます。
マンハッタン距離は、碁盤の目のように縦横にしか移動できない場合に使う距離です。
まるでニューヨークのマンハッタンの街を歩くように、交差点を曲がりながら目的地を目指すイメージです。
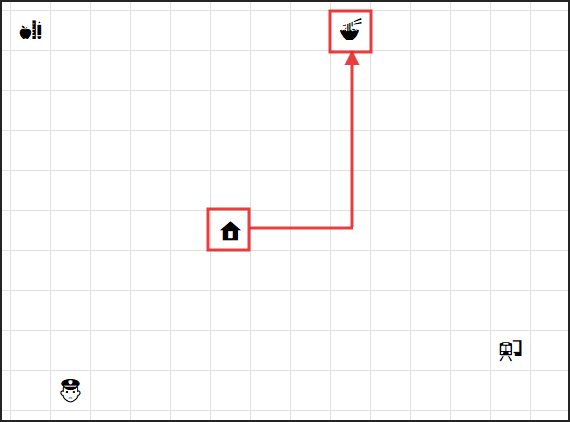
ユークリッド距離は、2点間を直線で結んだ場合の最短距離です。
普段私たちがイメージする「鳥が直線で飛んだ場合の距離」に近いです。
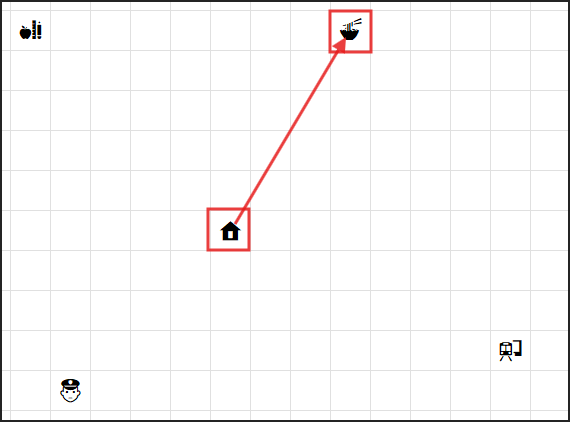
この2種類の距離を、Excelのマップ上で計算してみるのが今回のミッションです!
データの準備:セルで町づくり!
まずは、今回の遊びの舞台となる「Excelの町」を作ってみましょう。
といっても、難しい作業は一切なし!
セルを使って超シンプルなマップを作ります。
セルを正方形に調整する方法
より「町」っぽく見せるために、セルを正方形にしてみましょう。
Excelのデフォルト設定だと、列幅と行の高さが違うので、セルが横長の長方形になっています。
はじめに、シート全体を選択します。
(行番号と列番号の交わる左上の隅をクリック)
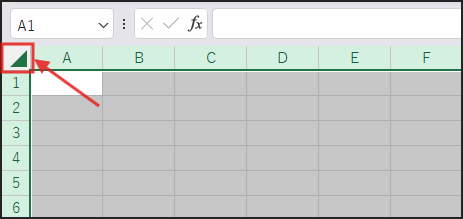
まず、列見出し(A, B, C…)の間の境界線にマウスポインタを合わせます。
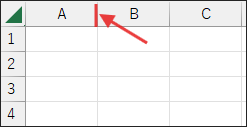
マウスポインタの形が左右の矢印に変わったら、そのままドラッグして列幅を好きな幅に調整してみましょう。
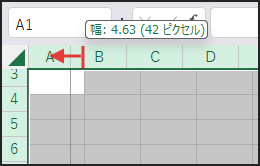
次に、行見出し(1, 2, 3…)の間の境界線にマウスポインタを合わせます。
マウスポインタの形が上下の矢印に変わったら、そのままドラッグして行の高さを調整してみましょう。
列幅と行の高さを、見た目で正方形になるように調整してみてください。
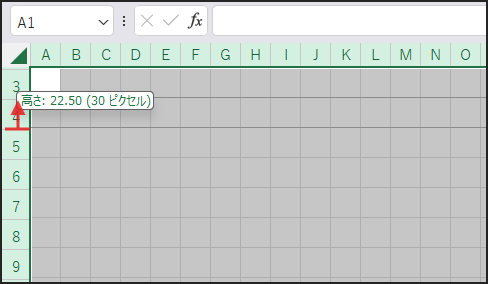
これで、Excelのセルがきれいな正方形になり、よりマップらしくなりました!
文字だけで建物を表現
次に、作ったマップの中に建物を配置してみましょう。
複雑な図形は使いません。
今回は、それぞれのセルに文字を入力するだけでOKです!
文字だけでなく、🏠や🌳といった絵文字を使ってみるのも面白いです。
見た目がぐっと楽しくなります!
例えば、
- 「家」
- 「公園」
- 「駅」
- 「学校」
- 「寺」
- 「??」(謎の場所!)
のように、好きな建物を好きな場所に文字で配置してみてください。

セルの背景色を変えたりするのも楽しいかもしれませんね。
シンプルだけど、遊べるマップ完成!
たったこれだけで、オリジナルのExcelマップが完成です!
このマップを使って、「家から公園まで」や「駅まで」の距離を計算してみるのが今回の目的です。
また、「謎の場所まで」の距離も計算してみましょう。
セルの距離ってどうやって測るの?
さて、いよいよ距離の計算に挑戦です。
まず、先ほど説明した2種類の距離について、もう少し具体的に見ていきましょう。
マンハッタン距離とユークリッド距離の直感的な違い
例えば、セル C3 にある「家」から、セル G5 にある「公園」までの距離を考えます。
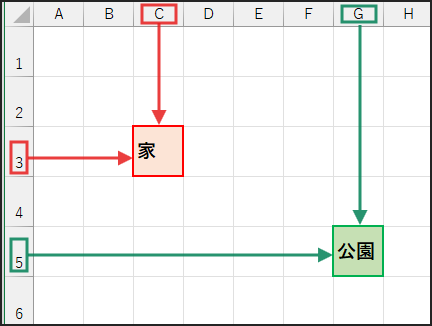
マンハッタン距離:セルからセルへ、上下左右の移動だけでたどり着く場合の最短距離です。
セル C3 から G5 へ移動するには、右に4マス(G列 – C列)、下に2マス(5行 – 3行)移動する必要があります。
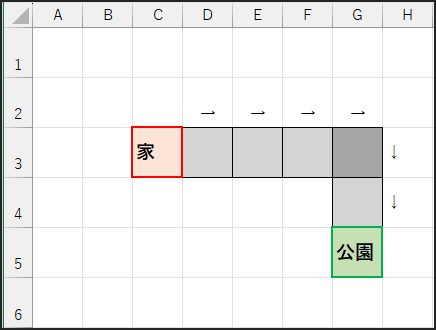
合計すると、4 + 2 = 6マスとなります。
曲がりくねった道を通っていくイメージですね。
ユークリッド距離:セル C3 から G5 をまっすぐ直線で結んだ場合の距離です。
斜めに移動するイメージです。

この距離は、三平方の定理(ピタゴラスの定理)を使って求めることができます。
先ほどの縦2マス、横4マスを辺とする直角三角形の斜辺の長さを求める感じです。
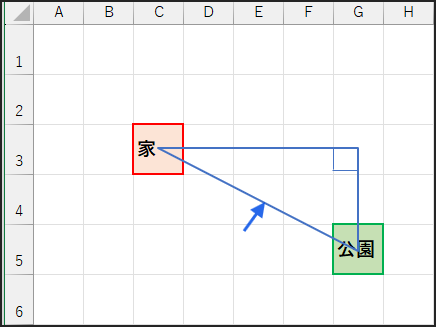
計算式は √(4^2 + 2^2) = √(16 + 4) = √(20) ≒ 4.47 マスとなります。
直感的に、マンハッタン距離は「道のり」、
ユークリッド距離は「直線距離」と考えると分かりやすいかもしれません。
それぞれExcelでどう表現できるのか
では、この2種類の距離をExcelで計算するには、どのような関数を使えば良いのでしょうか?
ここで今回の主役となる関数が登場します!
マンハッタン距離の計算
マンハッタン距離は、X方向(列)の移動距離とY方向(行)の移動距離をそれぞれ求めて、合計すれば良いんでしたね。
Excelでセルの位置を知るには、ROW() 関数と COLUMN() 関数が便利です。
ROW(セル番地):指定したセルの「行番号」を返します。COLUMN(セル番地):指定したセルの「列番号」を返します。
これらの関数を使って、例えばセル C3 からセル G5 までのマンハッタン距離を計算してみましょう。
=ABS(ROW(G5) – ROW(C3)) + ABS(COLUMN(G5) – COLUMN(C3))
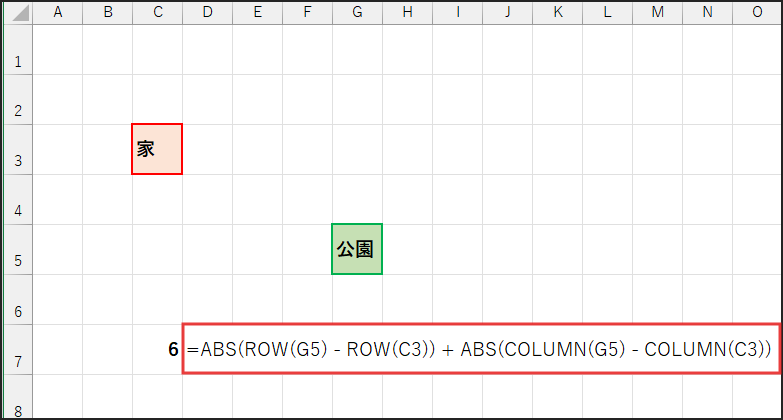
数式の解説
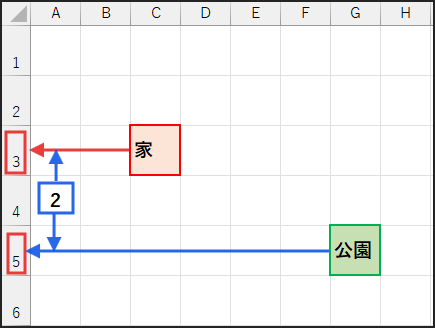
ROW(G5) – ROW(C3):目的地の行番号(5)からスタート地点の行番号(3)を引いて、
行方向の差(2)を求めています。
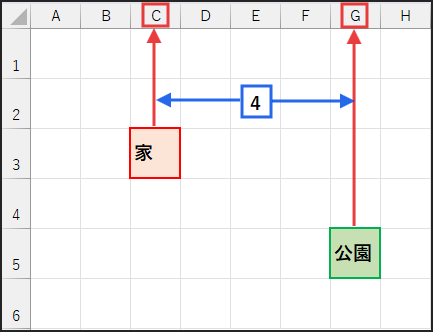
COLUMN(G5) – COLUMN(C3):目的地の列番号(7、G列は7番目)からスタート地点の列番号(3、C列は3番目)を引いて、列方向の差(4)を求めています。
ABS():絶対値を求める関数です。
距離なので、マイナスにならないように絶対値をとっています。
最後に、行方向の差と列方向の差を合計して、マンハッタン距離を求めています。
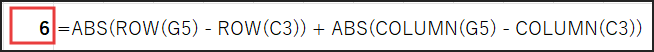
この数式をExcelに入力すれば、ちゃんとマンハッタン距離「6」が表示されるはずです!
ユークリッド距離の計算
ユークリッド距離は、先ほども触れたように √(列の差)^2 + (行の差)^2 で求められます。
Excelには平方根を求める SQRT() 関数があるので、それを使っても計算できます。
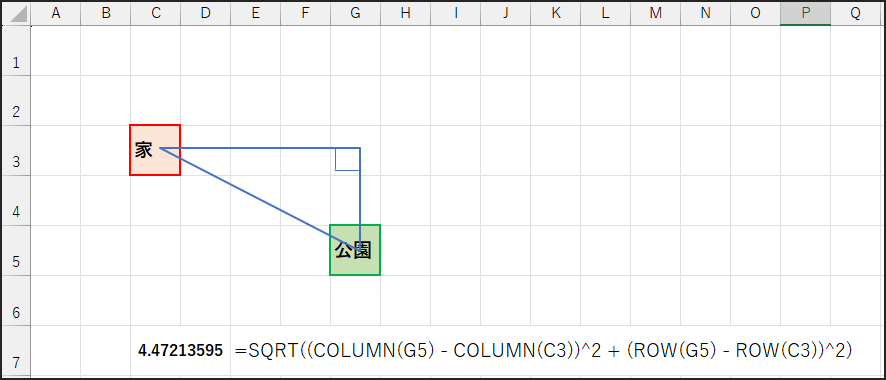
=SQRT((COLUMN(G5) – COLUMN(C3))^2 + (ROW(G5) – ROW(C3))^2)
(↑ SQRTを使ったユークリッド距離の計算例)
でも!
今回はもう一つ、面白い関数の組み合わせを紹介します。
それは、COMPLEX() 関数とIMABS() 関数を使う方法です!
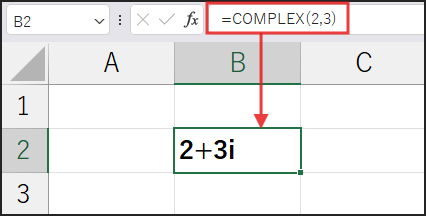
COMPLEX(実数部, 虚数部):指定した実数部と虚数部を持つ複素数を作成します。
複素数は、a + bi のような形で表される数で、実数部が a、虚数部が b の部分です。
IMABS(複素数):指定した複素数の「絶対値」を返します。
複素数 a + bi の絶対値は、
原点からの距離、つまり実数部と虚数部をそれぞれ二乗して足し合わせ、
その平方根をとった値となります。
この IMABS() 関数で複素数の絶対値を求める計算、どこかで見たことありませんか?
そう、ユークリッド距離の計算式 √(列の差)^2 + (行の差)^2 と同じ形をしていますよね!
ということは、
COMPLEX() 関数で「列の差」と「行の差」を実数部と虚数部にした複素数を作ります。
そして、その絶対値を IMABS() 関数で求めれば、ユークリッド距離が計算できる、ということです!
実際にセル C3 からセル G5 までのユークリッド距離を計算する数式を見てみましょう。
=IMABS(COMPLEX(COLUMN(G5) – COLUMN(C3), ROW(G5) – ROW(C3)))
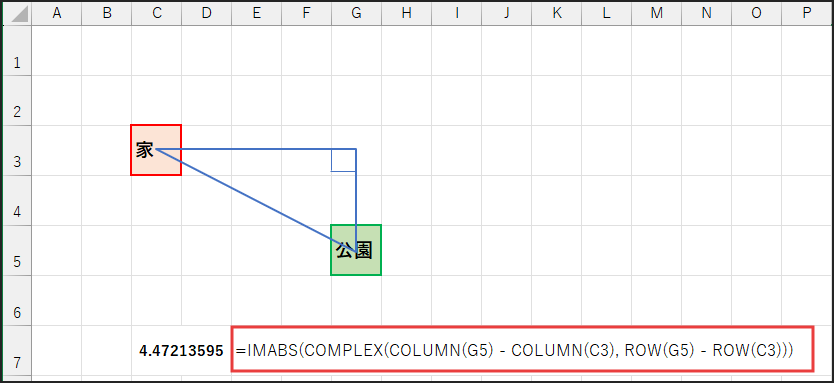
数式の解説
COLUMN(G5) – COLUMN(C3):列方向の差(4)を計算し、COMPLEX 関数の「実数部」に指定しています。
ROW(G5) – ROW(C3):行方向の差(2)を計算し、COMPLEX 関数の「虚数部」に指定しています。
COMPLEX(4, 2) は、複素数 4 + 2i を作成します。
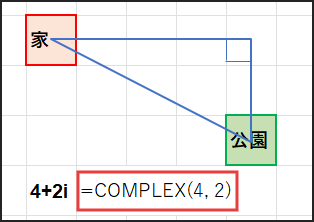
IMABS(COMPLEX(4, 2)) は、複素数 4 + 2i の絶対値 √(4^2 + 2^2) = √(16 + 4) = √(20) を計算します。
この数式をExcelに入力すると、ユークリッド距離である「4.47213562373095」(√20の近似値)が表示されるはずです!
距離の出し方いろいろ:どっちの関数が便利?
さて、マンハッタン距離には ROW() + COLUMN() + ABS()、
ユークリッド距離には COMPLEX() + IMABS() という関数の組み合わせが使えることが分かりました。
どちらの方法も距離を計算できますが、それぞれに特徴があります。
マンハッタン距離の計算は使っている関数も一般的で、計算過程も直感的で分かりやすいですね。
一方、ユークリッド距離を COMPLEX と IMABS で計算する方法は、複素数という普段あまり扱わない概念が出てくるため、最初は少し難しく感じるかもしれません。
でも、数式としては IMABS(COMPLEX(列の差, 行の差)) とコンパクトにまとまっていて、これはこれで美しい数式だと思いませんか?
=IMABS(COMPLEX(COLUMN(G5) – COLUMN(C3), ROW(G5) – ROW(C3)))
今回のテーマである「セルマップでの距離計算」という遊びにおいては、どちらの方法を使っても構いません。
マンハッタン距離を計算したい場面もあれば、ユークリッド距離を知りたい場面もあるでしょう。
もしあなたが「このセルからあのセルまでの直線距離を知りたい!」と思ったら、COMPLEX + IMABS の出番です。
そして、「どうしてこの関数で直線距離が出るんだろう?」と疑問を持ったら、
それが学ぶチャンスです!
複素数の絶対値がなぜ原点からの距離になるのか、少し調べてみるのも面白いかもしれません。
ぜひ、あなたのExcelマップで色々な場所の距離を計算しながら、「自分ならどっちの関数をどんなときに使うかな?」と考えてみてください。
実務でも役立つ!? この遊びが仕事に変わるシーン
「Excelでセルを町に見立てて距離を計算する遊び、面白かったけど、これって仕事で役に立つの?」
と思った方もいるかもしれませんね。
もちろん、この「遊び」そのものが直接仕事になるわけではありません。
でも、この遊びを通じて得られる「Excelのセルを座標に見立てる発想」や「位置情報から距離を計算する考え方」、
そして「普段使わない関数でも目的に合わせて活用してみる経験」は、様々なビジネスシーンで応用できるポテンシャルを秘めているんです。
例えば、
実務での応用例
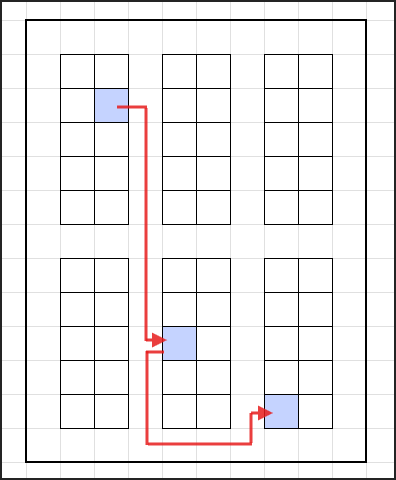
倉庫のレイアウト設計: 倉庫内の棚や商品の位置をセル番地で管理します。
そして、ピッキング作業者が最短距離で移動できるルートを計算します。
マンハッタン距離の考え方が役立つかもしれません。
営業ルートの最適化: 顧客の位置情報をExcel上で座標化し、訪問先間の移動距離を計算します。
こうすることで、効率的な営業ルートを検討できます。
店舗や施設の配置計画: 競合店や顧客の分布をExcelマップで表現します。
新しい店舗をどこに配置すれば多くの顧客から近くになるか、といった分析のヒントになります。
オフィス座席のシミュレーション: 部署間の物理的な距離を考慮して、コミュニケーションが取りやすい座席配置をシミュレーションします。
などなど、「位置」と「距離」が重要になるシーンはビジネスの中にたくさんあります。
今回の遊びのように、Excelのセルを柔軟に捉える発想が大切です。
そこにデータの「位置」を割り当てられれば、色々な分析やシミュレーションが可能になります。
特に、マンハッタン距離は倉庫内の通路のように直角にしか移動できない場所の距離計算に使えます。
ユークリッド距離は理論上の最短距離や、地図上の直線距離に近い分析に使えそうですね。
この「Excelでマップを作る」という発想自体が、
あなたのExcelスキルの幅を広げる大きな一歩になるはずです!
まとめ:Excelの中に広がる町を、あなたの関数で歩こう!
今回は、Excelのセルを町に見立ててマップを作りました。
そして、マンハッタン距離とユークリッド距離という2種類の距離を計算して遊んでみました。
今回はROW関数やCOLUMN関数、そしてCOMPLEX関数やIMABS関数といった、ちょっと聞き慣れない関数にも挑戦しましたね。
「Excelでこんなこともできるんだ!」
「この関数、面白いな!」
そう思っていただけたなら、とても嬉しいです。
遊びを通して、自然と新しい関数や概念に触れ、Excelの奥深さや面白さを感じてもらえたのではないでしょうか。
実は、今回計算した「マンハッタン距離」や「ユークリッド距離」は、AI(機械学習)がデータを分類する際(k近傍法など)にも使われる非常に重要な計算です。
Excelでこの感覚を掴んでおくと、データサイエンスの学習にも役立ちますよ!
これからも、Excelを使った楽しい「暇つぶし」や新しい活用法を見つけて、一緒に探求していきましょう!
また次回の暇つぶしでお会いしましょう!
以下の記事でも、複素数関数を使用しています!興味のある方は是非!
Excel縛りプレイ!関数のみで「i」を生成せよ




