Excel配列数式で「連続する塊」をカウントする方法

はじめに：この海に、島はいくつある？（2次元編）
アプローチ1：ラベリング法（進化の過程を見る）
アプローチ2：REDUCE関数一発で解く（魔法）
1. 数式の解剖図
まとめ：Excelは「計算機」を超えた

はじめに：この海に、島はいくつある？（2次元編）

以前の記事で、1列のデータから「連続する塊」を数える方法を紹介しました。
「なんだ、今回はその応用編か」と思いましたか？

Excelで「連続するデータの塊」を数える！0と1の島を探す6つの数式

いいえ、違います。今回は文字通り「次元」が違います。

1次元（列）の処理と、2次元（面）の処理では、難易度が桁違いです。

今回はExcel関数の限界に挑む、まさにラスボス級のミッションと言えるでしょう。

まず、A1:J10のセル範囲に、以下のような「0」と「1」のデータを用意します。

{0,0,0,1,1,0,0,1,0,1;1,1,0,1,1,0,1,1,1,1;1,1,0,0,1,1,0,1,0,1;0,1,1,0,1,0,1,0,0,0;0,0,0,0,0,0,1,1,0,0;0,1,0,1,1,0,0,0,0,0;0,0,0,0,1,0,1,0,1,1;1,1,1,1,1,0,1,1,1,1;1,0,0,0,0,0,0,1,0,0;1,0,1,1,0,0,0,1,0,0}

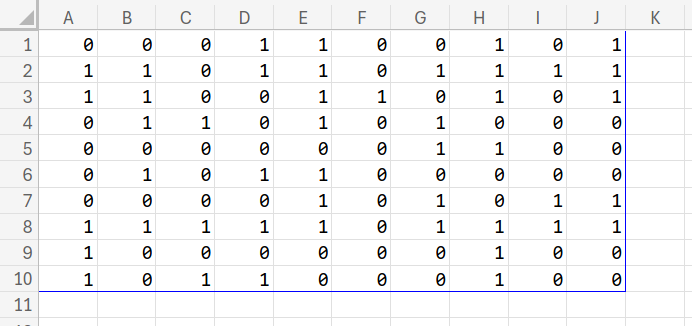
「1」を陸地、「0」を海として考えてください。

上下左右に陸地がくっついていれば、それは一つの「大きな島」とみなします。

【見た目の工夫】
単なる数字の羅列では分かりにくいので、条件付き書式を使って「1（陸）」を緑、「0（海）」を青に塗り分けています。
（※詳しい設定方法は割愛しますが、こうすることで「島の形」が直感的に見えてきます！）

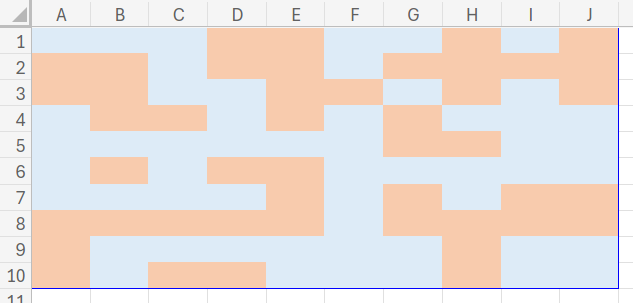
さて、この地図の中に「島」は全部でいくつあるでしょうか？

正解は「8個」です。

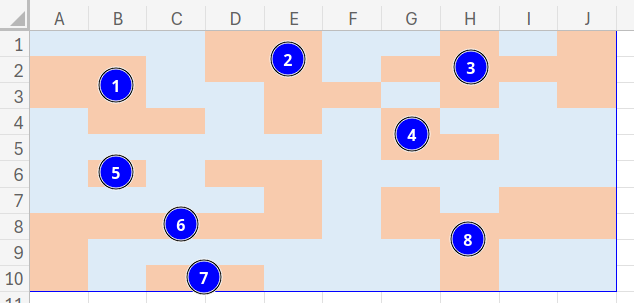
これを人間の目ではなく、Excelの関数だけで数えることはできるでしょうか？

これは情報工学の世界で「連結成分探索（Connected Component Labeling）」と呼ばれる、画像処理の基礎となる重要なアルゴリズムです。

今回は、この難問を解く2つのアプローチを紹介します。

【初心者向け】 作業用エリアを使って、じわじわと島を統合していく方法
【上級者向け】 最新関数 REDUCE を使い、たった一つの数式で答えを出す方法

アプローチ1：ラベリング法（進化の過程を見る）

本記事では、無料のWeb版Excelを使用して検証および画像の作成を行っています。Windowsはもちろん、MacやLinuxの方もブラウザさえあれば挑戦できます！
また、関数の詳細な仕様については、Microsoft公式のヘルプも参考にしてください。

はじめに、いきなり答えを出そうとせず、広い作業スペースを使って計算する方法です。

イメージは「すべての陸地に違う背番号をつけ、隣同士だったら小さい番号に統一していく」という陣取りゲームです。

ステップ1：作業用エリアの「枠」を作る

まずは、数式で「隣のセル」を見る際、端っこでエラーにならないよう、
データの周りを「0」で囲みます。

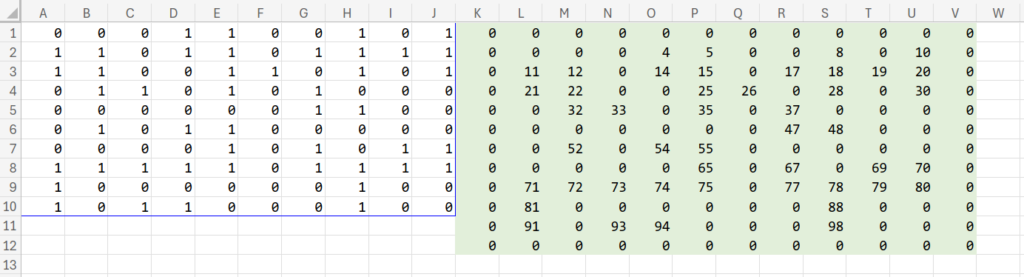
K1:V12 の範囲（12×12マス）を選択し、すべて 0 を入力してください。

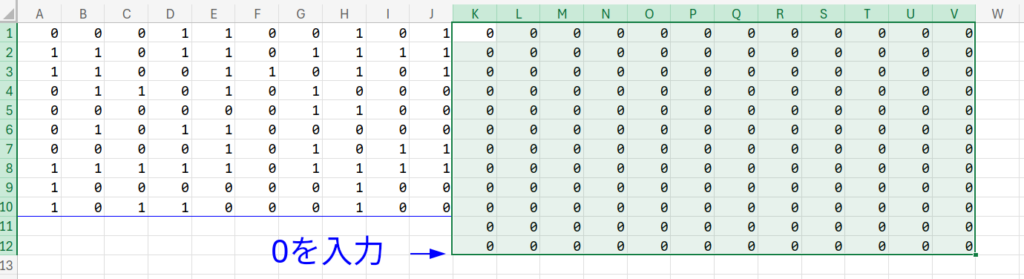
これが「第0世代（初期状態）」のエリアになります。

外周（K列、V列、1行目、12行目）は最後まで0（海）の防波堤として機能します。

ステップ2：初期IDを振る（第0世代）

次に、海（0）はそのまま、陸（1）にはユニークな背番号（ID）を振ります。

内側の L2セル を選択し、以下の数式を入力します。

=IF(A1=0, 0, (ROW(A1)-1)*10 + COLUMN(A1))

【解説】
元のデータ（A1）が0なら0。

1なら、行番号と列番号を使って固有のIDを作ります。

例えば A1なら「1」、A2なら「11」、B1なら「2」になります。

このL2セルを、L2:U11 の範囲（10×10）にコピペします。
これで、すべての陸地がバラバラのIDを持った状態（第0世代）が完成しました。

ステップ3：融合させる（第1世代の作成）

続いて、ここから進化の計算です。
すぐ右隣のエリアを使います。

まず、W1:AH12 の範囲（12×12マス）を選択し、すべて 0 を入力して枠を作ります。

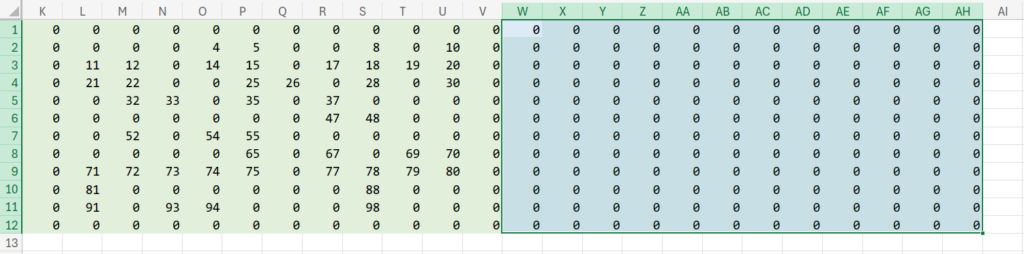
続いて、その内側の X2セル（左上）を選択し、以下の数式を入力します。

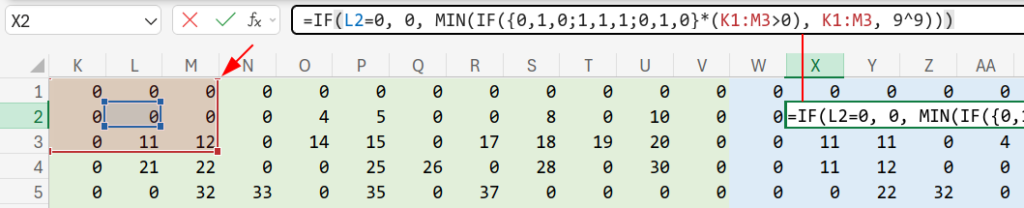
=IF(L2=0, 0, MIN(IF({0,1,0;1,1,1;0,1,0}*(K1:M3>0), K1:M3, 9^9)))

【解説：ここが心臓部！】
この数式は、「自分（L2）」と「上下左右の隣人（K1:M3）」を見渡しています。

{0,1,0;1,1,1;0,1,0}：これは十字型のマスクです。自分と上下左右だけを「1」にします。

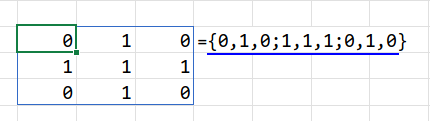
これにより、「斜めはつながっていない（4近傍）」というルールを表現しています。

MIN(..., 9^9)：十字の範囲内にいる「海(0)以外の陸地」の中で、最も小さいIDを採用します。

つまり、「隣に自分より小さい番号のやつがいたら、その番号に染まる」という処理です。

このX2セルを、X2:AG11 の範囲（10×10）にコピペします。
これで、隣り合った陸地同士でIDが統合された「第1世代」が完成しました。

ステップ4：ひたすら繰り返す（第2世代以降）

あとは、この「進化（統合）」を数字が変わらなくなるまで繰り返します。

W1:AH12 の範囲（第1世代のエリア全体）をコピーします。
※外枠の0も含めてコピーするのがコツです。
すぐ右隣の AI1セル に貼り付けます（第2世代）。
さらに右隣の AU1セル に貼り付けます（第3世代）。

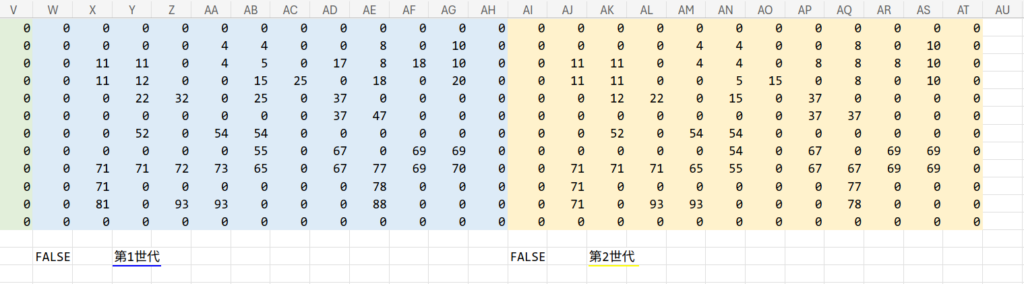
これを繰り返していくと、つながっている陸地はどんどん同じ番号（その島の中で最小の番号）に統一されていきます。

【収束の確認】
W14セルあたりに =AND(K1:V12=W1:AH12) という数式を入れて、一緒に右へコピペしていくと便利です。
この値が TRUE になった時が、「もう変化しない＝全ての島がつながった」合図です。

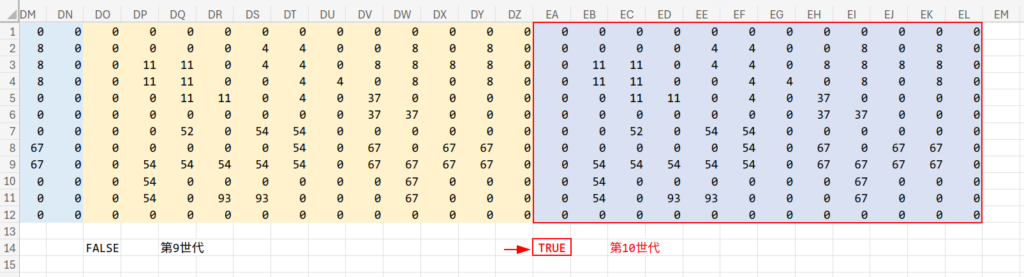
ステップ5：島の数を数える

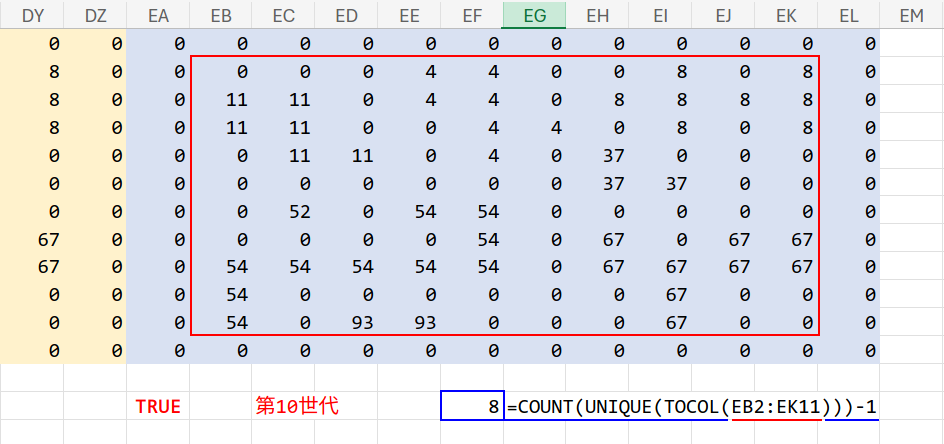
最後に、一番右側に貼り付けたエリア（TRUEになったタイミング。仮に EA1:EL12 だとします）を使って、答えを出します。

=COUNT(UNIQUE(TOCOL(EB2:EK11)))-1

【解説】
1. TOCOL：計算結果を1列に並べます。ここで範囲を EB2:EK11 にしているのは、外枠の「0（防波堤）」を除外して、中身の10×10マスだけを集計するためです。
2. UNIQUE：重複を消して、残ったIDの種類だけにします。
3. COUNT：その個数を数えます。
4. -1：最後に、海である「0」の分を引きます。

これで「8」という答えが出れば大成功です！

アプローチ2：REDUCE関数一発で解く（魔法）

「手動でコピペなんてスマートじゃない！」

そんな上級者のために、最新関数 REDUCE を使って、上記のプロセスをメモリ上ですべて処理する数式を紹介します。

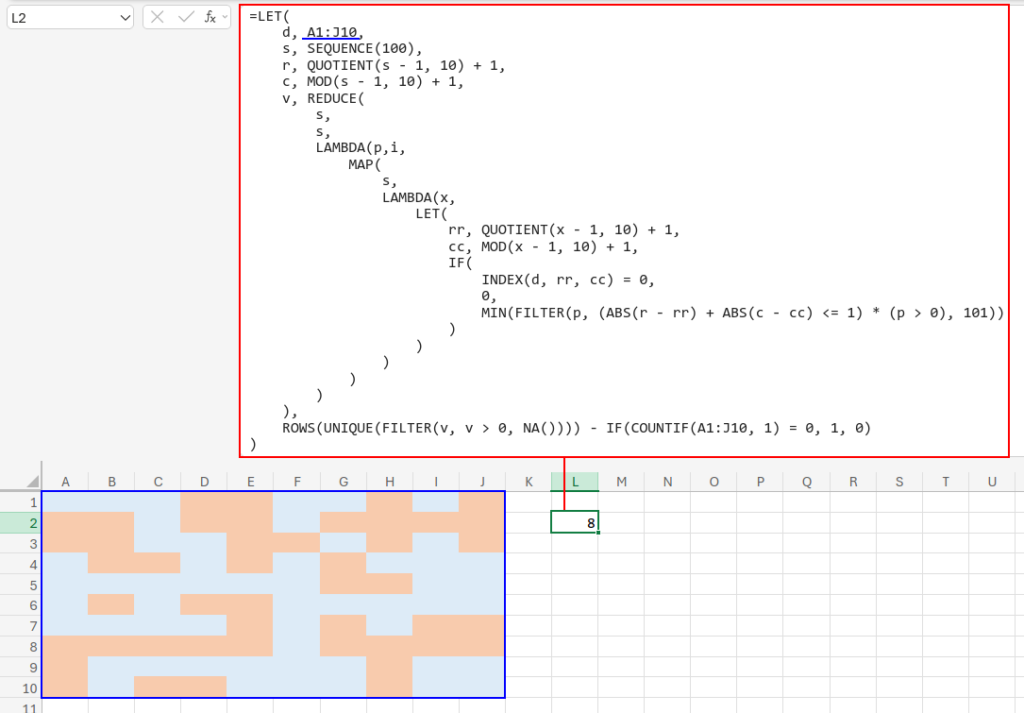
=LET( d,A1:J10, s,SEQUENCE(100), r,QUOTIENT(s-1,10)+1, c,MOD(s-1,10)+1, v,REDUCE(s,s,LAMBDA(p,i, MAP(s,LAMBDA(x, LET( rr,QUOTIENT(x-1,10)+1, cc,MOD(x-1,10)+1, IF(INDEX(d,rr,cc)=0,0, MIN(FILTER(p,(ABS(r-rr)+ABS(c-cc)<=1)*(p>0),101)) ) ) )) )), ROWS(UNIQUE(FILTER(v,v>0,NA())))-IF(COUNTIF(A1:J10,1)=0,1,0) )

数式の解剖図

やっていることは、アプローチ1とほぼ同じなので解説画像は省略します！

1. 世界を作る（座標の準備）

s, SEQUENCE(100) で、まず1から100までの連番（初期ID）を作ります。
これがステップ2の「初期ID」にあたります。

r と c は、そのIDが10×10グリッドのどこにあるかを示す「行番号」と「列番号」です。

2. 時間を進める（REDUCE）

REDUCE(s, s, LAMBDA(p, i, ...))
これが「右へ右へとコピペする作業」の代わりです。

初期状態 s に対して、LAMBDA の中の計算（融合処理）を繰り返します。

【なぜ REDUCE(s, s, ...) なの？】
第2引数に s（SEQUENCE(100)）を指定しているのは、「100回繰り返す」という意味です。
もし陸地が「一筆書きの迷路」のように長く蛇行していた場合、情報が端から端まで伝わるのに時間がかかります。
実際には100回もかかることはありませんが、念の為、マスの総数（100回）だけ繰り返しておけば間違いがないため、あえてこの回数に設定しています。