本記事では、Excel 2021を使用して検証および解説を行っています。
素数をExcel関数だけでリスト化してみよう!
「Excelで素数? そんなことして何になるの?」
そう思った方もいるかもしれませんね!
もちろん、日常業務で膨大な素数リストをExcel関数だけで作る場面は…、
まあ、ほとんどないでしょう(笑)
でも、今回の目的はそこではありません!
目的は、「一見難しそうに感じることでも、条件を分けて考えれば答えは出せる」ということを経験することです。
普段あまり使わない関数の意外な使い方や、
一見複雑に見える処理をどうやって関数だけで組み立てていくのか。
その過程を、まずは体験してみましょう!
今回は、「2から100000までの素数をリストアップする」という課題に、
Excelの関数だけで挑戦します!
このチャレンジを通して、あなたのExcel関数スキルが、
また一歩前進するきっかけになるかもしれませんよ!
今回のミッション
現在の状態とゴール
現在の状態: 空白のExcelシート
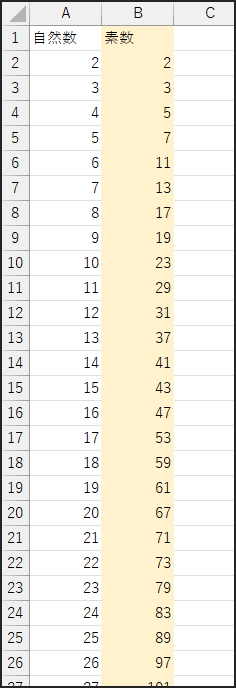
目指すゴール: 以下の画像のように、
B列に関数だけで「2から100000までの素数」を表示させること。
ルール:関数以外使用禁止!
- 使用するのはExcelの「関数」のみです。VBA(マクロ)などは使いません。
- 作業列を好きなだけ使ってOKです!
- 最終的な素数リストはB列に表示させます。(1行目は見出しとします)
- Excel 2021で使用できる関数のみを使用します。(筆者の環境に合わせます!すみません…)
さあ、準備はいいですか?
関数の力を使って、素数探索の旅に出発しましょう!
素数リスト!初心者向け・作業列活用テクニック
はじめに、計算のステップごとに作業列を使って、処理の流れを分かりやすくする方法を紹介します。
考えかた
そもそも素数とは、
「1とその数自身以外に約数を持たない、1より大きい整数」のことですね。
1は素数ではありません。約数が1つしかないため。
ある数Nが素数かどうかを調べるには、2から順番にNを割っていきます。
ただし、Nより小さい数すべてで割ってみる必要はありません。
実は、Nを「ある数」で割るとき、その「ある数」を2回掛けた数(ある数 × ある数)がNを超えたら、それ以上調べる必要はないんです。
それまでに、2を含めて一度も割り切れなければ、
その数Nは素数だと言えます。
例えば、Nが13の場合、
まず2で割ると割り切れません。
次に3で割っても割り切れません。
次の「ある数」は4ですが、4×4=16で13を超えてしまうので、
ここでチェックは終わりです。
13は2でも3でも割り切れなかったので、素数だと分かります。
この考え方に基づいて、以下のステップで進めます。
1. A列:チェック対象となる自然数のリスト(2から100000まで)を作成
2. C列:各自然数の平方根を計算
3. D列:平方根の整数部分(割り算チェックの上限)を計算
4. E列:2から平方根(整数部分)までの数で割り切れるか(=合成数か)をチェック
5. B列:E列のチェック結果をもとに、素数だけを抽出して表示
このように、段階を踏んで計算していくのがこの方法の特徴です。
手順
A列 – 自然数のリストを作成
まず、素数かどうかをチェックしたい数字のリストを用意します。
今回は2から100000までです。
A2 セルを選択します。
次に、数式バーに以下の数式を入力して [Enter] を押します。
=SEQUENCE(99999,1,2,1)
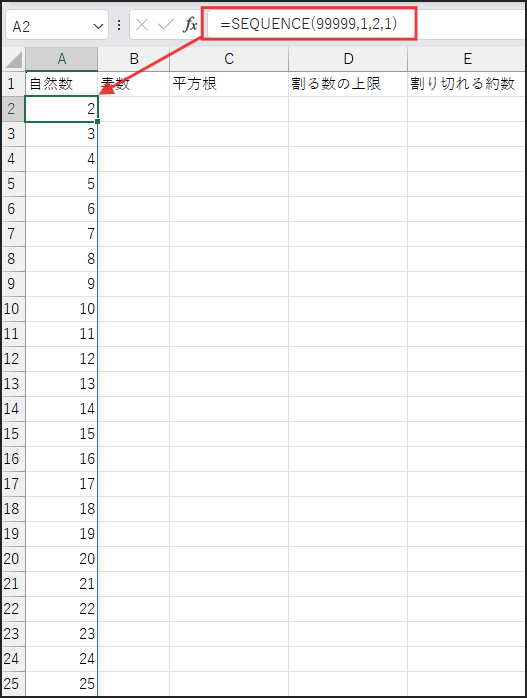
これにより、A2セルから下に、2, 3, 4, …, 100000 という連続した数値が自動的に入力されます。(スピル機能)
SEQUENCE(行数, [列数], [開始番号], [増加値]) は、連続した数値の配列を生成する関数です。
ここでは、99999行×1列で、開始番号2、増加値1の数値を生成しています。
C列 – 「平方根」の計算
続いて、素数判定の効率化のため、A列の各数値の平方根を計算します。
C2 セルを選択してください。
そして、数式バーに以下の数式を入力します。
=SQRT(A2)
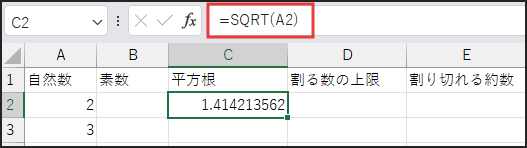
入力後、C2セルの右下にあるフィルハンドル(■)をダブルクリックするか、
下方向にドラッグします。
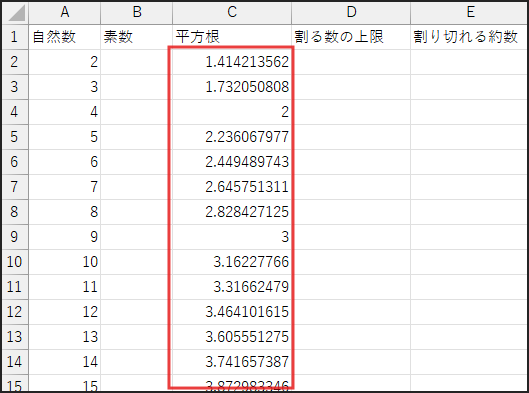
これで、A列に数値がある範囲まで数式がコピーされます。
SQRT(数値) は、数値の正の平方根を返します。
D列 – 「割る数の上限」の計算
次に、平方根の整数部分を求めます。
素数判定では、この整数部分までで割り算チェックをすれば十分です。
D2 セルを選択してください。
数式バーに以下の数式を入力します。
=INT(C2)
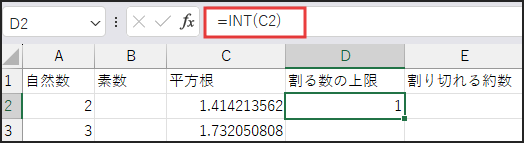
C列と同様に、D2セルの数式を下方向にコピーしてください。
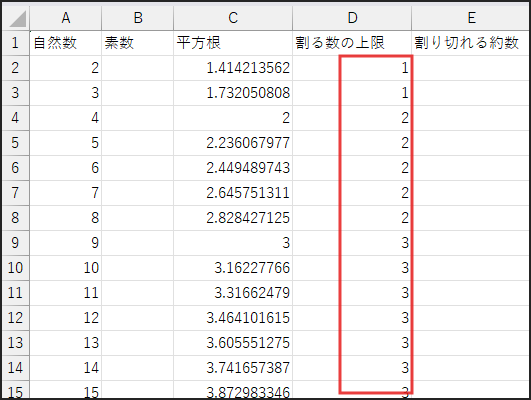
INT(数値) は、数値の小数点以下を切り捨てて整数部分を返す関数です。
E列 – 「割り切れる約数があるか?」のチェック
いよいよ素数判定の核心部分です!
A列の数値が、2からD列の数(平方根の整数部分)までのいずれかで割り切れるかどうかをチェックします。
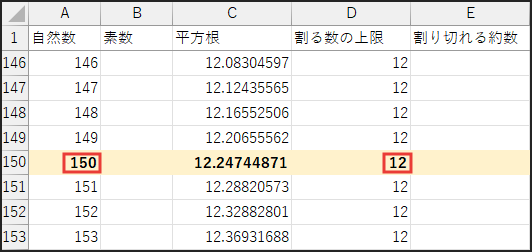
150÷2,150÷3,…,150÷12 のように、割り切れるかどうかをチェック!
割り切れるものがあれば「合成数」、
なければ「素数」という判定になります。
まず、E2 セルを選択します。
そして、数式バーに以下の数式を入力します。
=IF(D2<2, FALSE, OR(MOD(A2, SEQUENCE(D2-1, 1, 2))=0))
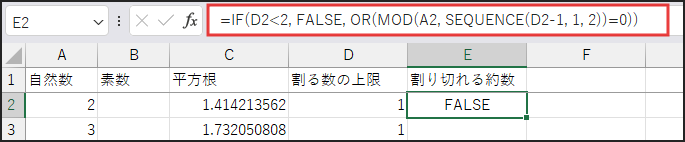
入力したら、E2セルの数式を下方向にコピーします。
素数判定の数式解説
この数式は少し複雑では?
分解して考えてみましょう。
まず、IF(D2<2, FALSE, …) の部分です。
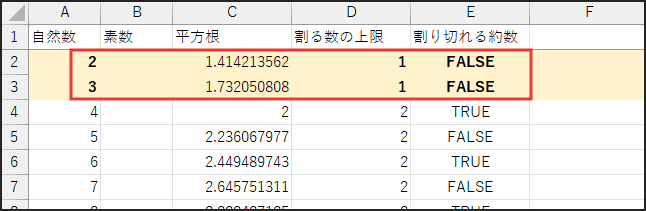
これは、D2が2未満の場合、無条件で FALSE (素数扱い) とするための処理です。
そして、メインとなるのが OR(MOD(A2, SEQUENCE(D2-1, 1, 2))=0) の部分です。
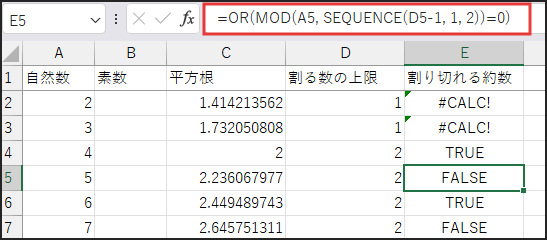
SEQUENCE(D2-1, 1, 2) で、2からD2までの連続した整数の配列(割る数のリスト)を作ります。
挙動がわかりやすいように、以下、自然数 122 の場合の画像です。
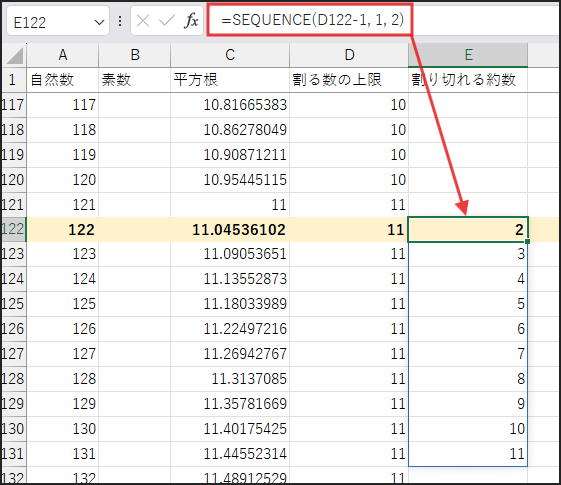
MOD(A2, …) で、A2を割る数のリストの各数値で割った余りを計算します。
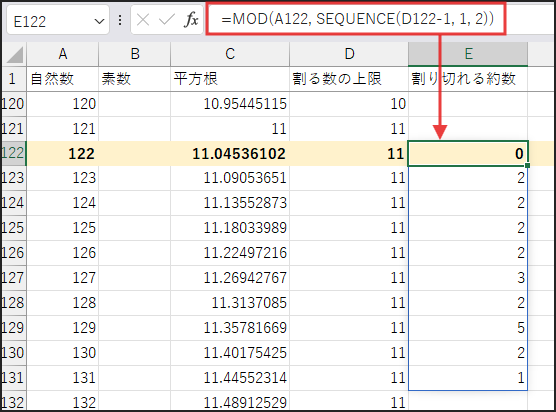
… = 0 で、余りが0になる(つまり割り切れる)かどうかを TRUE/FALSE の配列で判定します。
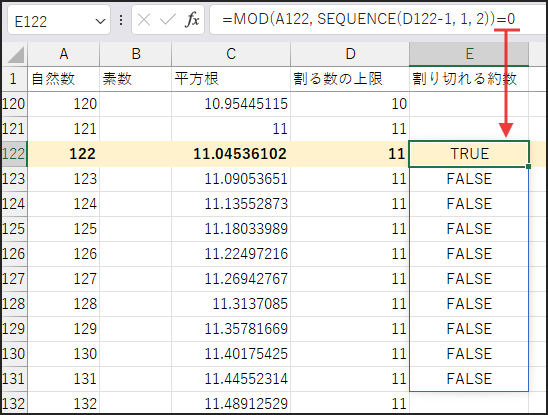
最後に、OR(…) で、その配列の中に一つでも TRUE があれば TRUE を返します。
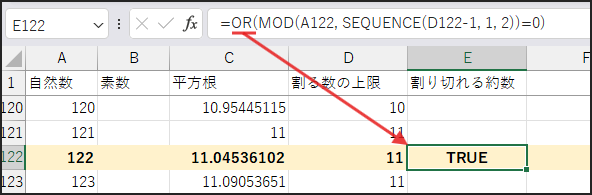
すべて FALSE なら FALSE (=素数) を返します。
結果として、このE列には「合成数なら TRUE、素数なら FALSE」が表示されることになります。
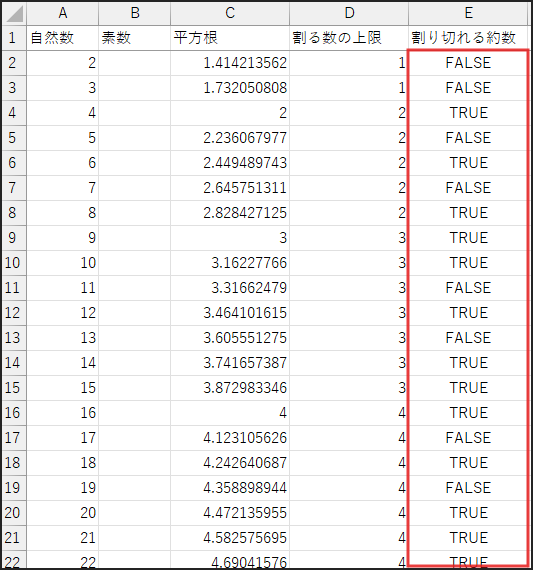
B列 – 素数リストの表示 (最終結果)
最後に、E列が FALSE (素数) であるA列の数値を、目的のB列に抽出します。
B2 セルを選択します。
数式バーに以下の数式を入力して [Enter] を押します。
=FILTER(A2:A100000, E2:E100000=FALSE)
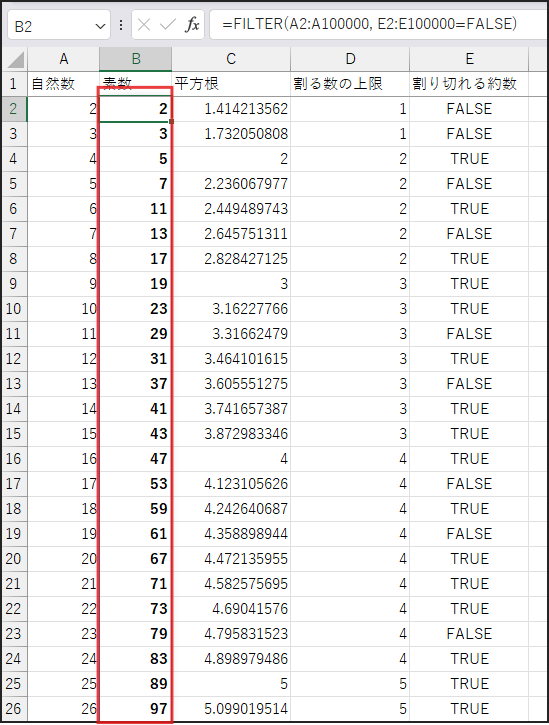
FILTER(配列, 条件) は、配列の中から条件に一致する要素だけを抽出する関数です。
ここでは、A2からA100000の範囲から、対応するE2からE100000がFALSEであるものだけを抽出しています。
動作確認
ここまでの手順が正しくできていれば、B列に、2, 3, 5, 7, 11, 13, … と順番に素数が表示されるはずです。
ただし、100000までの計算には少し時間がかかるかもしれません。
解説
この方法の最大の特徴は、素数判定のロジックを各作業列に分解している点です。
これにより、処理の流れが追いやすいというメリットがあります。
使用している関数を見ると、SEQUENCE関数やFILTER関数といった比較的新しい関数が活躍していますね。
これらと、SQRT、INT、MOD、ORといった基本的な関数を組み合わせることで、目的を達成しています。
一つ一つの関数の役割を理解しながら進められるため、
初心者の方にも比較的取り組みやすい方法と言えるでしょう。
メリット&デメリット
- メリット:
- 各ステップが列ごとに分かれており、処理内容を理解しやすい点。
- 意図しない結果になった場合、どの列の計算に問題があるか特定しやすいこと。(デバッグが容易)
- デメリット:
- 計算のために複数の作業列 (C, D, E列) が必要になり、シートが少し煩雑に見える可能性。
- 計算ステップが多いこと。(ただし、必ずしもExcel内部の処理が非効率とは限らない)
素数を作業列なしでスッキリ表示!
次に、作業列を使わない方法に挑戦してみましょう。
一つの数式(をコピーしていく形式)だけで素数リストを作成する、
なかなか難易度の高い方法です!
考えかた
この方法では、前の行で見つけた素数をもとに、
次の素数を探索するというアプローチを取ります。
具体的には、配列数式の機能や、普段あまり目にしない関数の組み合わせ(例えばMMULT関数など)を駆使します。
作業列を使わない分、数式は非常に複雑になりますが、
配列数式の強力さを垣間見ることができます。
準備
まず、新しいシートを用意します。(例えばSheet2など)
次に、A1 セルに 見出しとして「素数」と入力します。
そして、A2 セルに 最初の素数である 2 を入力しておきます。
これで準備は完了です。
手順
A3セルに数式を入力
ここが核心部です!
以下の非常に長い数式を A3 セルに入力してください。
=SMALL(IF(ROW(INDIRECT(A2+1 & ":" & A2*2)) > 1, IF(MMULT(N(MOD(ROW(INDIRECT(A2+1 & ":" & A2*2)), TRANSPOSE(ROW(INDIRECT("2:"&INT(SQRT(A2*2)))))) = 0), ROW(INDIRECT("2:"&INT(SQRT(A2*2))))^0) = 0, ROW(INDIRECT(A2+1 & ":" & A2*2)))), 1)
数式をコピー
数式を入力したら、A3セルを選択します。

最後に、A3セルの右下にあるフィルハンドル(■)を下方向にドラッグして、必要な行数までコピーします。
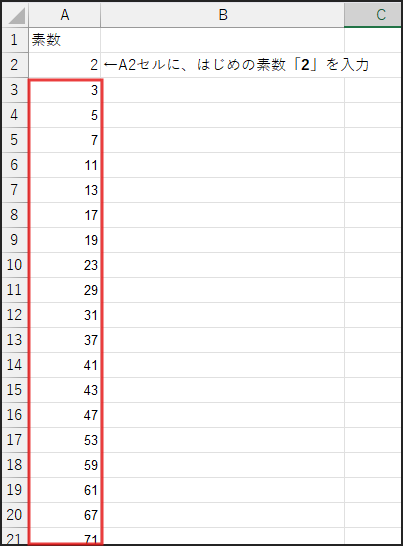
動作確認
正しく入力・コピーできていれば、A列に、2, 3, 5, 7, … と順番に素数が表示されていくはずです!
【注意】 この数式は非常に計算負荷が高いです!
そのため、あまり多くの行にコピーすると、Excelの動作が極端に遅くなったり、応答しなくなったりする可能性があります。
試す際は、少しずつコピーすることをお勧めします。
解説(数式のざっくり説明)
この数式は、複雑な処理を行っています。
ざっくり言うと、以下のような流れです。
まず、INDIRECT関数やROW関数を使って、一つ前の素数 A2 を基準に、次の素数が存在しそうな範囲(例えばA2+1 から A2*2 まで)を動的に生成します。
次に、MMULT関数やMOD関数などを複雑に組み合わせて、その探索範囲内の各数値が素数かどうか(つまり、2からその数値の平方根までの整数で割り切れないか)を判定します。
最後に、IF関数で素数判定の結果をフィルタリングし、SMALL関数を使って、条件を満たす(=素数である)数値の中で最小のものを、次の素数としてA3セルに返します。
正直なところ、この数式を理解するのはなかなか大変です!
(数式を作った人でさえも、正確に理解するまで時間がかかります。)
まさに「関数パズル」の極みと言えるかもしれません。
メリット&デメリット
- メリット:
- 作業列が不要なため、シートの見た目は非常にすっきりする点。
- MMULT関数や配列数式の非常に高度で強力な使い方を体験できること。
- デメリット:
- 数式が難解であり、内容の理解や修正が困難な点。
- 計算負荷が非常に高く、多数の素数を生成しようとするとExcelがフリーズする可能性があること。(実用的ではない)
- 一つ前のセル (A2) に依存するため、リストの途中の数式を削除したりすると正しく計算できなくなること。
まとめ
今回は、「Excelの関数だけで素数リストを作成する」という、少し変わった課題に挑戦してみました!
作業列を使う方法1は、処理の流れが追いやすく、
SEQUENCE関数やFILTER関数といった便利な関数の使い方も学べましたね。
一方、作業列を使わない方法2は、実用性は低いものの、配列数式やMMULT関数がいかに複雑な計算を実現できるかを示す、興味深い例でした。
実務で素数リストが必要になる場面は少ないかもしれません。(多分、ありません!)
しかし、このような一見無駄に見える挑戦を通して、思考力や応用力が鍛えられます。
例えば、
「この処理を実現するには、どの関数をどう組み合わせればいいか?」
「配列ってどういう動きをするんだろう?」
「もっと効率的な数式の書き方はないかな?」
といった考え方です。
普段何気なく使っているExcel関数ですが、その組み合わせ次第で様々な可能性が広がっています。
実務ではシンプルで分かりやすい方法を選びつつ、たまにはこうした一見無駄に見える挑戦で頭の体操をするのも面白いかもしれません。
今回の探求が、皆さんのExcel関数への興味や理解を深める一助となれば幸いです!