Excelで遊んでいる皆さん、こんにちは!
今回も、ちょっと変わったExcelの「暇つぶし」に挑戦してみませんか?
今回のテーマは、皆さんおなじみ「あみだくじ」です。
ただ、いつものあみだくじとは少し違います。
一番上に、左から順に 1、2、3、……、10 と数字が並んでいます。
そして、一番下には、なぜか順番が逆になった 10、9、8、……、1 と数字が並んでいます。
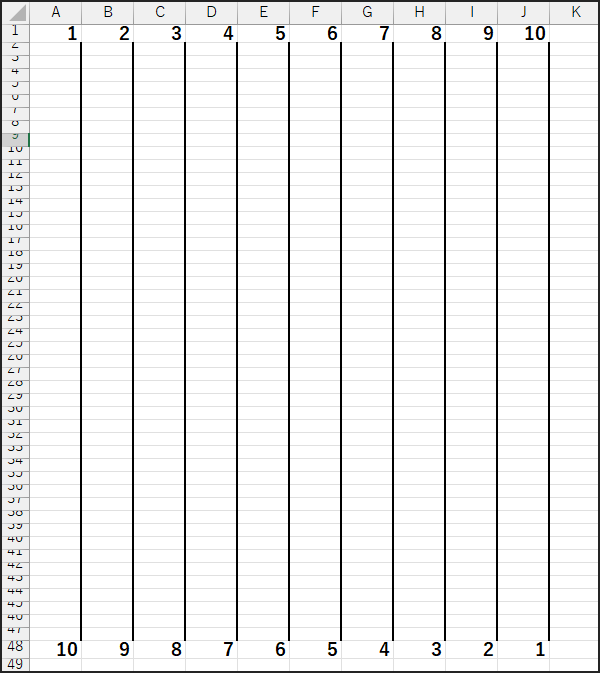
さて、ここで問題です!
この上と下の数字を、あみだくじの「横線」を使って、
正しいもの同士(上の1と下の1、上の2と下の2のように)でつなぎたいのです。
あなたなら、どこに線を引きますか?
線を引けるのは、縦線と縦線の間だけです。
そこに「横線」を自由に引いてみましょう。
ぜひ、Excelを開いて、試しに数字を並べて手を動かしてみてください。
線を引く代わりにセルの色を変えたり図形を置いたりして、
ちょこっと作業してみるのも面白いかもしれませんよ?
さあ、一緒に頭の体操を始めましょう!
はじまり!今回のミッション!
今回のミッションはとてもシンプルです。
Excelシート上で、1から10まで順に並んだ数字があります。
これを、見た目としての横線を引くことで、逆順の10から1までにつなげることです。
これは、見た目はあみだくじですが、実はある「並べ替え」をシミュレーションしています。
どんな線を引けば、上の数字と下の逆順の数字が正しくつながるのか?
ぜひ、あなたの手で挑戦してみてください!
ステップ1:まずは自由に線を引いて遊んでみよう!
小さな数で試す
「よし、やってやるぞ!」と思って、いきなり1から10まで並べて考えると、
少し大変かもしれませんね。
まず、もっと少ない数で試してみるのはどうでしょう?
たとえば、1、2、3 と並んでいて、下は 3、2、1 にしたい場合です。

あるいは、1、2、3、4、5 で、下は 5、4、3、2、1 にしたい場合です。

Excelで試してみたい!
という方のために、簡単なサンプルファイルをご用意しました!
excel_de_himatsubushi021.xlsx (15KB)
自由に試行錯誤
縦に並んだ数字の隣に、自由に横線を引いてみてください。
セルの色を変えるとか、罫線を引くとか、やりやすい方法でOK!
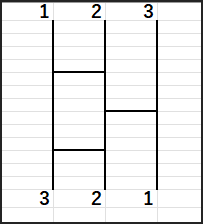
そして、一番上の数字からスタートして、引いた線を通って下までたどり着くと、
どの数字にたどり着くか?
これを追ってみましょう。
線を足してみたり、消してみたり…。
「あれ?思っていたのと違う…」
「うーん、あと少しでつながるんだけどなぁ」
なんて試行錯誤を繰り返すのが、この段階の楽しいところです!
正解をすぐに求めず、まずは自由に、
好きな場所に線を引いて遊んでみてくださいね(笑)
まるで迷路を進むみたいで、
意外と時間が経つのを忘れちゃうかもしれません。
ステップ2:あれ?これって法則があるのかも?
試行錯誤の後に生まれる疑問
自由に線を引いて遊んでいたら、もしかしたらこう思い始めた方もいるかもしれません。
「なんとなく線を引いていたけど、これって何か法則があるのかな?」
「やみくもに線を引くより、何か考え方があるのかも…?」
そうなんです!
実はこのあみだくじ、ただの遊びではないのです。
線を引くことで、数字の「順番」を入れ替えていますよね。
隣同士の「swap」に注目!
ここで少しだけヒントです!
線を1本引くと、その線の左右にある縦線の経路が入れ替わり、
結果として下の出口の数字が入れ替わったようになるイメージ、分かりますか?
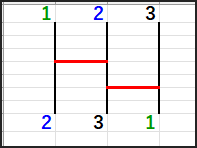
たとえば、1 | 2 | 3 と並んでいて、1と2の間の縦線に横線を1本引くと…。
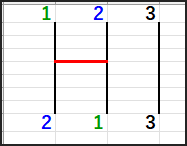
たとえば、一番上の1からスタートして線を通ると、
本来たどるはずだった1の縦線から2の縦線に移動し、
2からスタートした場合は1の縦線に移動します。
こうして、線を通ることで隣り合った縦線の経路が入れ替わり、結果としてたどり着く出口が入れ替わったように見えます。
そう!
まるで、隣同士の数字を「swap(スワップ)」しているような動きになるのです。
もしかして、この「隣同士のswap」を繰り返せば、どんな順番でも作れる…?
そして、今回の目標である「完全逆順」も、このswapの組み合わせでできる…?
頭の中で、あるいはExcelシートの上で、この「swap」の動きをイメージしてみてください。
なんとなく見えてきたかもしれません。
しかし、まだ答えは言いませんよ!(笑)
ステップ3:みんなの「できた!」を見てみよう
色々な「できた!」例
試行錯誤の末、「できた!」という方もいると思います。
線をたくさん引いた!
という方もいれば、
意外と少なくできた!
という方もいるかもしれませんね。
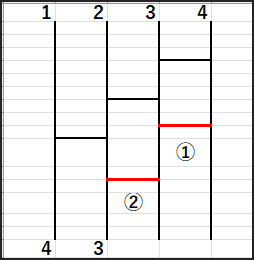
たとえば、このように線が多く引かれていると…
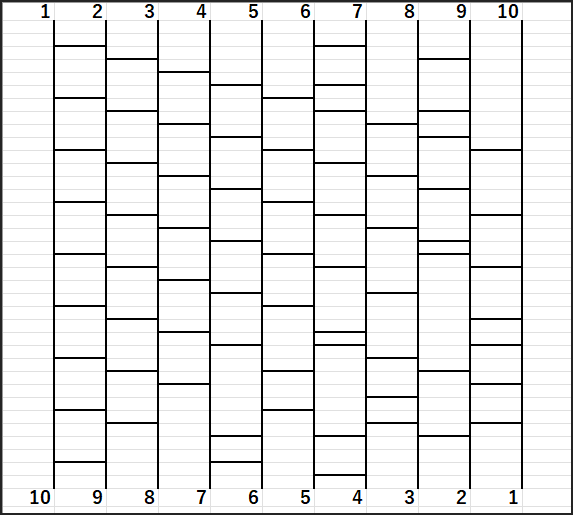
上の1は下の10へ、上の2は下の9へ…という具合に、きちんと逆順につながっています。
逆に、このように線が少なめに「できた!」という例もあります。
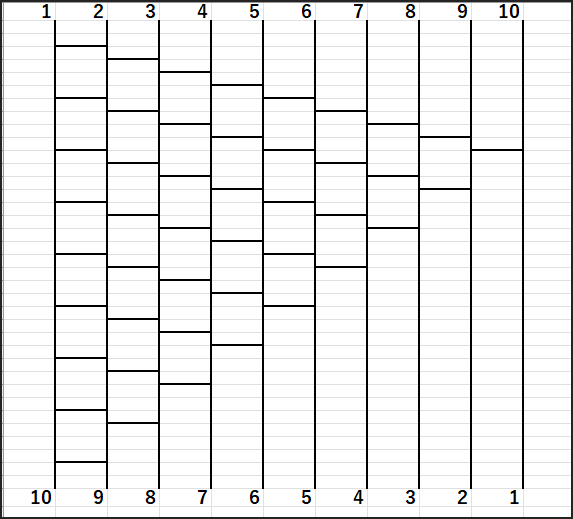
こちらも、きちんと逆順につながっていますね!
自分のやり方と比較してみよう
自分の考えた線の引き方と比べてみてどうでしょう?
「あ!このようにすればもっとシンプルになるのか!」とか、
「私のやり方、意外と効率悪かったかも?」
なんて、新しい発見があるかもしれません。
でも、大丈夫です!
この段階では、どのような線の引き方でも「できた!」ことが素晴らしいのです。
みんなで一緒に、それぞれのやり方を「振り返る」くらいの優しい気持ちで見てみましょうね。
ステップ4:最低、何本必要なの?完全逆順に必要な本数は?
さて、色々な線の引き方で「完全逆順」が実現できることが分かりました。
ここで、もう一つ大きな問いを投げかけてみましょう!
私たちが目指す「1, 2, …, 10」から「10, 9, …, 1」への完全逆順。
この並べ替えを実現するために必要な「横線の数」、つまり「swapの回数」、
最低何本だと思いますか?
「え?まだ線減らせるの?」
「自分が引いた線、もっと少なくできるの!?」
そう思ったあなた!
きっともう一度、Excelシートを見直したくなってきたのではないでしょうか?(笑)
ここから先は、「最低限の本数」を探る旅です。
どのようにすれば無駄なく、効率的にswapを繰り返せるのか?
一緒にその謎に迫ってみましょう!
ステップ5:小さな数字で「なぜ?」を解き明かそう!
法則を見つけるための実験
最低本数を見つけるために、また小さい数で考えてみるのが近道です。
たとえば、1、2、3 を 3、2、1 にする場合です。

隣同士のswapで考えましょう。
隣同士のswapで考える
ここでは、理解を深めるために、横線を引く操作を「隣り合った数字(の経路)を入れ替える操作」として捉えてみましょう。
これは、コンピュータの世界の並べ替えで使われる「隣接する要素の交換(swap)」に相当します。
完全逆順にするには、どのようにswapしていけば効率が良いでしょうか?
nの場合の手順:n=3
まず、3を一番左に持ってくるために、1 | 2 | 3 から始めます。
まず、2と3の間でswapして、1 | 3 | 2 とします。
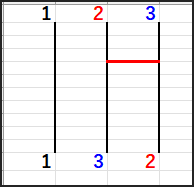
次に1と3の間でswapして、3 | 1 | 2 とします。
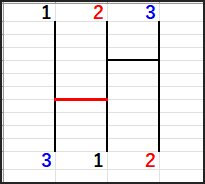
これで3は一番左、定位置に来ました。
続いて、残った 1と2 を入れ替えます。
これで完成です!
1と2の間でswapして、3 | 2 | 1 とします。
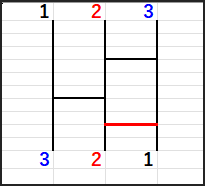
必要なswapは、最初の段階で2回、次の段階で1回の、合計3回です。
nの場合の手順:n=4
次に、1、2、3、4 を 4、3、2、1 にする場合を考えます。
まず、右端の4を一番左に持ってくるために、(4-1) = 3回のswapが必要です。
はじめに、3と4の間でswapします。
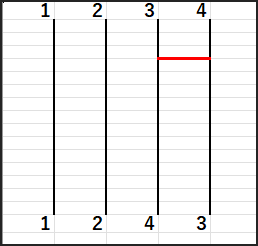
次に2と4の間でswapします。
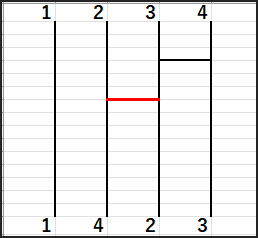
最後に1と4の間でswapします。
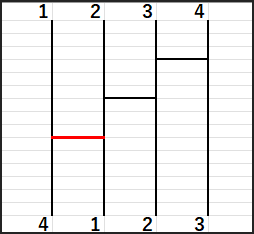
これで4は一番左に来ました。
続いて、残った 3、2、1 の中で、3を一番左(全体の2番目)に持ってくるのに、(3-1) = 2回のswapが必要です。
まず2と3の間でswapします。
次に1と3の間でswapします。
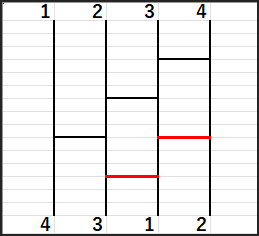
これで3は定位置に来ました。
次に残った 2、1 の中で、2を一番左(全体の3番目)に持ってくるのに、(2-1) = 1回のswapが必要です。
1と2の間でswapします。
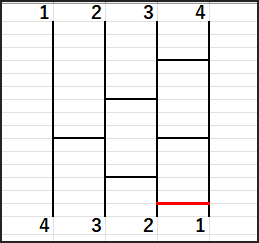
最後に残った1は自然と定位置につきました。
合計で、3 + 2 + 1 = 6回のswapが必要になります。
解説:必要なswap回数のパターン
右端から順番にswap
なるほど!
だんだん法則が見えてきましたね!
完全逆順にするには、右端から順番に数字を、
その場所に来るまでに必要な回数だけ隣とswapしていくイメージです。
右端の数字を一番左に動かすのに (n-1) 回です。
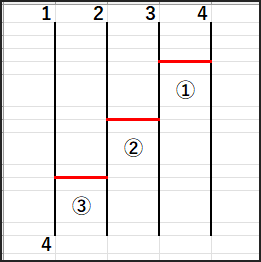
その次に右端だった数字を2番目に動かすのに (n-2) 回です。
…という具合にswapを繰り返します。
swap回数の合計パターン
必要なswapの合計回数は、以下の計算で求められます。
(n-1) + (n-2) + …… + 1
これは、1から(n-1)までの数字をすべて足し合わせた数ですね。
この合計は、数学の世界では有名な公式 n × (n-1) / 2 で求めることができます。
ステップ6:あみだくじは「ソート」だった!?法則を一般化!
法則を一般化する
小さな数字での実験から見えてきた法則を、いよいよ一般化してみましょう。
最低swap回数の公式
n個の数字を完全逆順に並べ替えるために必要な最低swap回数は、
公式: n × (n-1) / 2 で求めることができます。
つまり、今回の 1から10までの数字 (n=10) を完全逆順にするのに必要な最低swap回数は…
10 × (10 – 1) / 2 = 10 × 9 / 2 = 90 / 2 = 45回
そう!
最低でも 45本の横線 が必要なんです!

解説:あみだくじとソートの関係
あみだくじはswapの可視化
どうでしょう?
予想より多かったですか?
少なかったですか?
単純なあみだくじ遊びだと思っていたら、実はその裏で、数字の並び替え(コンピュータの世界では「ソート」と呼ばれます)の基本原理である「バブルソート」のような動きが隠れていたのです!
あみだくじで線を引く行為は、まさにこの「隣同士のswap」を可視化している、
と言えるかもしれませんね。
他の並べ替えの場合
他の並べ替え(たとえば、1, 3, 2, 4 など)でも、必要なswap回数は変わってきます。
興味があれば、ぜひ他のパターンでも考えてみてください!
まとめ:線を引く遊びの奥に、考える楽しさがあった!
記事の振り返り
今回は、あみだくじを使って数字の順番を入れ替える遊びを通して、
その裏に隠された論理や数学に触れてみました。
好きな場所に線を引く、という単純な遊びから始まりましたが、
さまざまな疑問が生まれたはずです。
どのようにすれば目的の並べ替えができるかな?
もっと効率的なやり方があるかな?
最低何回swapすればできるのだろう?
あれ?
小さい数で試すと何か法則が見えるぞ?
ということは、
大きい数でも同じ法則が使えるはずだ!
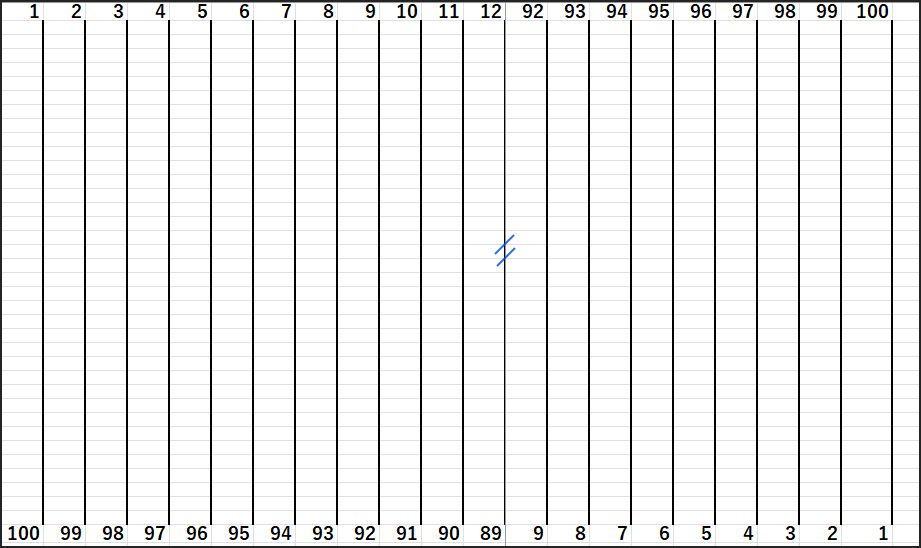
(n = 100のときは 4950本必要ですね!)
考える楽しさを見つけよう
「なぜ?」という疑問が生まれ、それを試行錯誤しながら解き明かしていく過程が、
何よりも楽しかったのではないでしょうか。
Excelは、ただ計算したり表を作ったりするだけでなく、
今回のようにちょっとした「遊び場」として、
論理的に考えたり、法則を見つけたりするためのツールにもなるのです。
ぜひ、今回の「あみだくじ順序入れ替え」を応用して、
別の数字の並べ替えで遊んでみてください。
必要な横線の数はいくつになるかな?
どのように線を引けば最短でできるかな?
新しい発見が、きっとあるはずです!
これからも、Excelを使った楽しい「暇つぶし」を見つけて、一緒に探求していきましょう!
また次回の暇つぶしでお会いしましょう!
理屈はわかったけど、Excel関数で一瞬で並べ替えたい!」という方は、こちらの記事をどうぞ。
Excel関数で「重複しないランダムな数値」を作る3つの方法!抽選や席替えに