ギターの音、もしかして「気持ち悪い」?Excelで解き明かす音の秘密
まず、ギターを弾く皆さん、こんな経験ありませんか?
「ハーモニクスでチューニングしたのに、なんかコードの響きが気持ち悪い…」
「5弦の7フレットハーモニクスと4弦の5フレットハーモニクス、合わせたはずなのにオクターブ上が微妙にズレてる気がする…」
「特に6弦と1弦、同じEのはずなのに、なんかこう…しっくりこないんだよなぁ…」
そう、それ、気のせいじゃないんです!
あなたの耳は決して悪くありません。
むしろ、その微細な「気持ち悪さ」を感じ取れるあなたは、素晴らしい耳の持ち主です!
そして、この長年のモヤモヤ、実はめちゃくちゃ奥が深い、
知的好奇心をくすぐるExcelパズルで解き明かせるって知ってましたか?
「え、Excelでギターのチューニングの謎が解けるの!?」
そうなんです!
今回の「暇つぶし」では、小難しい音楽理論書を紐解くのではなく、我らが愛する表計算ソフト・Excelを駆使して、この音の「気持ち悪さ」の正体を徹底的に、数値で暴き出していこうという、ちょっぴりマニアックな試みなんです(笑)
さて、今回の目的は、決して「これが絶対正しいチューニングだ!」と声高に叫ぶことではありません。
そうではなく、「なぜ、完璧に合わせたはずの音がズレて聞こえるのか?」
その原因を、Excelというツールを使って、まるで実験でもするかのように、とことん解析してみる「壮大な暇つぶし」なんです!
あなたがこれまで「なんとなく」感じていた音のズレを、
Excelのセル上に「数値」としてハッキリと映し出し、「見える化」する。
これって、なんだかワクワクしませんか?
最終目標は、ただギターが上手くなることだけじゃありません。
ギターの音、音楽の仕組み、そしてExcelというツールの無限の可能性を、あなた自身の力で「遊び倒す」こと。
そんなマニアックな楽しさを、この記事を通して共有できれば最高です!
さあ、「音のズレ」を探る冒険へ、一緒に出発しましょう!
音の正体と人間の耳:Excelで「周波数」と「比」を扱う
さて、ここから壮大な「暇つぶし」の始まりです!
まず初めに、我々がこれからExcelでいじくり回す「音」の正体と、
それを人間がどう感じ取っているのか、その基本的なルールをExcelと絡めておさらいしましょう。
ここをしっかり押さえておくと、後の音律の話がググッと面白くなりますよ!
音の物理的単位「Hz(ヘルツ)」とExcelでの表現
ご存知の通り、音は空気の振動であり、その振動の速さ(1秒間に何回振動するか)を「周波数」と呼び、単位はHz(ヘルツ)で表されます。
周波数が高ければ高い音、低ければ低い音、というのは直感的にも分かりますよね。
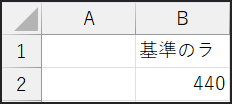
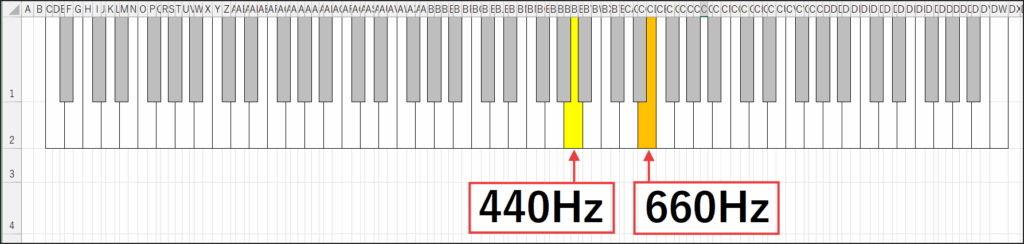
例えば、多くのチューナーで基準とされる「A(ラ)」の音は440Hzです。
これをExcelで表現するのは簡単!
適当なセル、例えばセルB2に440と入力すれば、それが「基準となるラの音の周波数」を表している、と我々が決めればいいだけの話です。
このように、Excelのセルは、音の高さという物理現象を「数値」として扱うための、最初のとっかかりになってくれるわけです。
まあ、ここまではウォーミングアップですね!
人間が感じる音程は「比」が命!対数とExcel
ここからが重要です!
音の高さそのものは周波数という「絶対的な数値」で表せますが、
我々人間が感じる「音程(インターバル)」、つまり2つの音の高さの「隔たり」は、
実は周波数の「差」ではなく「比」で決まるんです!
「え、差じゃなくて比?」
そうなんです!
ここ、めちゃくちゃ大事なポイントなので、もう一度言います。
音程は「比」が命!
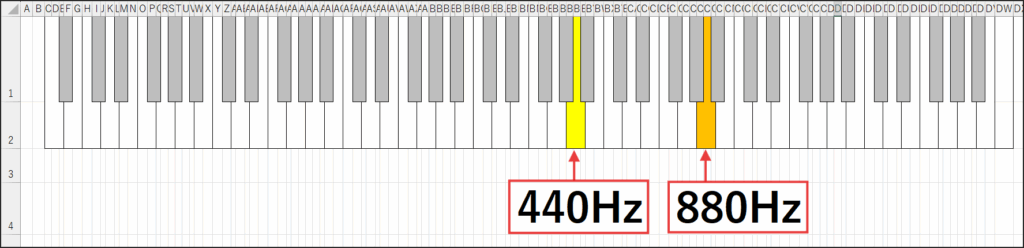
例えば、先ほどの440Hzのラ(A4)の音。
この1オクターブ上のラ(A5)の音の周波数は、皆さんご存知の通り880Hzですよね。
では、A4とA5の周波数の「差」は880 - 440 = 440Hzです。
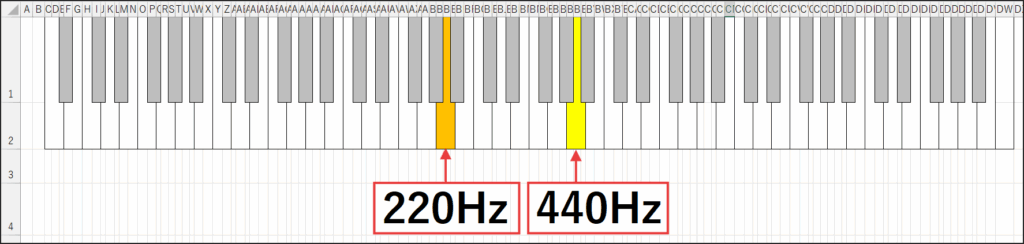
一方、A3(220Hz)とA4(440Hz)の周波数の「差」は440 - 220 = 220Hzです。
「差」は全然違いますよね?
でも、我々の耳にはA3→A4も、A4→A5も、
同じ「1オクターブ」という音程として認識されます。
これが「比」が重要である証拠!
A4に対するA5の周波数比は 880 / 440 = 2
A3に対するA4の周波数比も 440 / 220 = 2
そう、周波数比が同じ「2倍」だから、同じ「1オクターブ」に聞こえるのです!
他の音程も見てみましょう。
例えば、ド(C)に対するソ(G)の音程は「完全5度」と呼ばれ、非常に協和する美しい響きです。
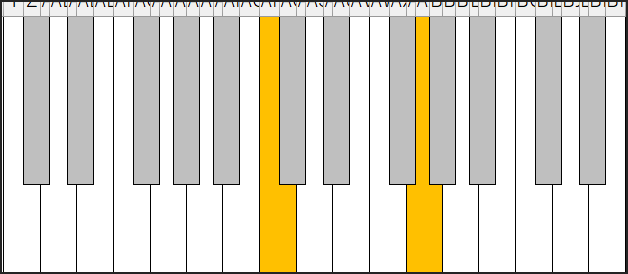
この完全5度の周波数比は、だいたい3:2、つまり1.5倍の関係になっています。
ラの音(A=440Hz)の完全5度上のミ(E)の音は、440 * (3/2) = 660Hzとなります。
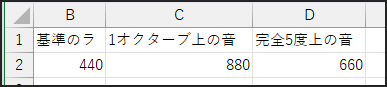
これをExcelで計算するのは超簡単!
セルB2に基準周波数440が入っているとしたら、1オクターブ上の音は、セルC2に=B2*2と入力すればOK。
完全5度上の音は、セルD2に=B2*3/2または=B2*1.5と入力すれば計算できます。
そして、ここで「おや?」と思ったあなたは鋭い!
人間が音程を「比」で感じているということは、
私たちの感覚は「線形」ではなく「対数的」である可能性を示唆しています。
「対数…? 高校数学でやったアレか…?」
そうです、アレです!
ExcelにもちゃんとLOG関数が用意されていますよね。
実はこのLOG関数、後の「セント」という音のズレを精密に測る単位を計算するときに、とんでもなく重要な役割を果たすことになるんです!
今の段階では「ふーん、LOGねぇ…」くらいで大丈夫。
Excelのセル上で、基準の音の周波数に様々な「比」を掛け算していくことで、色々な音の高さを作り出し、それらを比較していく。
これが、これから始まる音律探求の基本操作になります。
ワクワクしてきましたか?
音律の三巨頭!「純正律」vs「ピタゴラス音律」vs「平均律」をExcelで徹底比較分析
さあ、いよいよ本日のメインディッシュの一つ、音律の世界へ足を踏み入れましょう!
「音律って何だっけ…?」
という方もご安心を。
簡単に言えば、「ドレミファソラシド」といった音階の各音の周波数を、どのような「比」の関係で定めるか、というルールのことです。
歴史上、様々な音律が考案されてきましたが、今回は特に重要な「純正律」「ピタゴラス音律」「平均律」の三つをExcelで徹底的に比較分析し、それぞれの特徴と「ズレ」の正体を暴き出します!
純正律:「最も美しく響く和音」の理想郷?
まず登場するのは「純正律(Just Intonation)」です。
その名の通り、「純正な響き」、
つまり「最も美しく協和する和音」を作り出すことを目指した音律です。
その秘密は、各音の周波数比がごく単純な整数比で構成されている点にあります。
例えば、ドミソの和音(長三和音)が美しく響くのは、ド(1)に対してミが5/4倍、ソが3/2倍という、非常にシンプルな整数比になっているからです。
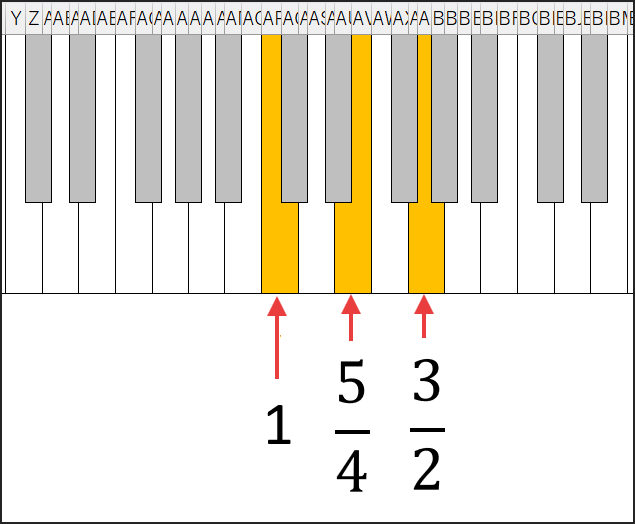
Excelワークシートを「純正律計算機」に!
では、実際にExcelを使って、純正律の音階を計算してみましょう。
基準となる音を、ここではA4=440Hzとします。
そして、このAの音を基準(1/1)として、主要な純正律の音程の周波数を計算していきます。
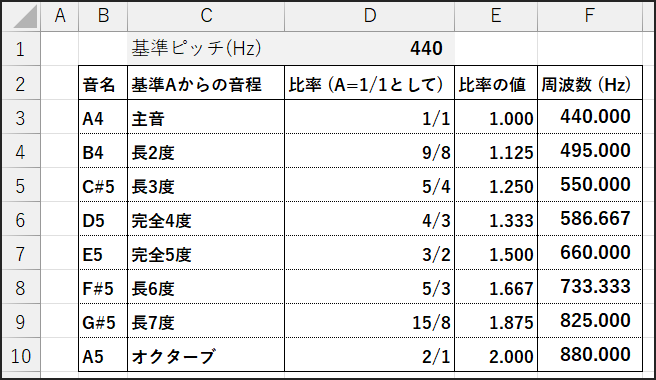
どうですか?
Excelの得意技である計算と表作成のおかげで、一見複雑そうな純正律の音階も、その比率さえ分かっていれば簡単に再現できてしまいますね!
この「単純な整数比」こそが、純正律の和音が澄み切った美しい響きを持つ理由なのです。
しかし、この純正律、実は大きな問題を抱えています。
それは「転調に弱い」ということ。
ある調で完璧に美しく響くように調整すると、他の調では途端に響きが悪くなってしまうのです。
うーん、なんとも悩ましい!
まさに「理想郷」は一つ所に留まれない運命なのでしょうか。
ピタゴラス音律:3倍音が生み出す「完全なる5度」の世界と、その「影」
次に登場するのは、古代ギリシャの哲学者であり数学者でもあるピタゴラスの名を冠した「ピタゴラス音律(Pythagorean Tuning)」です。
この音律の最大の特徴は、完全5度(周波数比3:2)の響きを絶対的に重視し、それを積み重ねて音階を作り上げていく点にあります。
ギターを弾く皆さんならピンと来るかもしれませんが、
弦の長さの2/3の場所(または1/3の場所)で得られるハーモニクス音は、元の音の完全5度上の音(の1オクターブ上、つまり周波数3倍)になりますよね。
「ハーモニクスで合わせた音は、このピタゴラス音律に近い響きを持っている」と、まずは頭の片隅に置いておいてください。
これが後々の「なぜハーモニクスチューニングがズレるのか?」という謎を解く鍵の一つになります!
Excelでピタゴラス音律の各音を計算!
ピタゴラス音律の計算は、まさにExcelの独壇場!
基準音(仮にCとしましょう。周波数は後で決めます)から、完全5度(3/2倍)を上に積み重ねたり、完全4度(4/3倍、これは5度下をオクターブ上げたものと解釈でき、実質的に(2/3)倍してオクターブ調整)を下に積み重ねたりして音を作っていきます。
例えば、Cを基準(1)とすると、GはC * (3/2)
DはG * (3/2)(オクターブ調整が必要なら1/2倍) → C * (3/2) * (3/2) = C * (9/4)
オクターブ調整してC * (9/8)
AはD * (3/2)→C * (9/8) * (3/2) = C * (27/16)
EはA * (3/2)→C * (27/16) * (3/2) = C * (81/32)
オクターブ調整してC * (81/64)
という具合です。
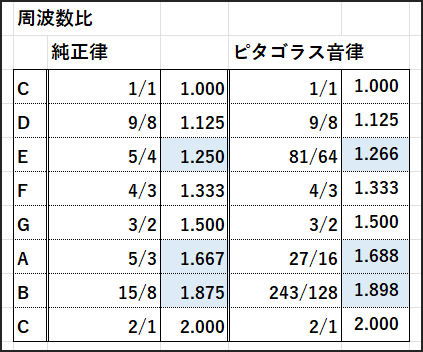
さて、このピタゴラス音律、完全5度は非常に美しいのですが、大きな「影」も持っています。
それは、特定の3度の響きがかなり不協和になるという点です。
特に問題となるのが「長3度」
純正律ではド(1)に対するミ(E)の比率は5/4(=1.250)で、非常に澄んだ響きでしたよね。
ところがピタゴラス音律では、Cから完全5度を4回積み重ねて作られるEの音は、
Cに対して (3/2)^4 をオクターブ調整したもの、つまり (81/64) (=1.265625)という比率になります。
5/4 = 80/64
ピタゴラスの長3度 = 81/64
この81/64と80/64のわずかな差、(81/64) / (80/64) = 81/80
これを「シントニック・コンマ」と呼びます。
数値で見ると大したことないように感じますか?
いやいや、これが和音になると、結構「うなる」ような濁った響きを生み出してしまうのです!
Excelでこの二つの長3度の周波数(例えばC4=261.63Hzを基準に)を計算し、その差を具体的に見てみましょう。
純正律 E:=261.63 * (5/4)→327.0375 Hz
ピタゴラス E:=261.63 * (81/64)→331.1255... Hz
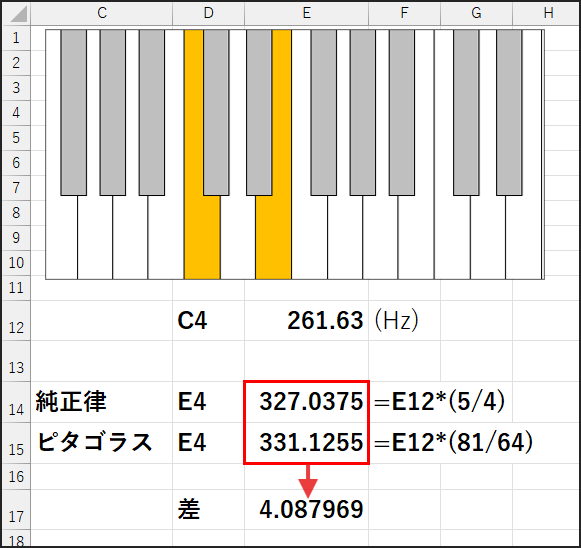
この差、約4Hz!
このズレが、ピタゴラス音律の「影」の部分。
完全5度の純粋さを追求した代償とも言えるでしょう。
「なるほど、だからハーモニクスで合わせた音が、なんだか特定の和音だと気持ち悪かったのか…?」
その通り!
その疑問に、Excelが数値という形で一つの答えを提示してくれましたね!
平均律:万能音律
そして、現代のピアノやギターで最も一般的に使われているのが「平均律(Equal Temperament)」です。
「どんな調でも同じように、そこそこ問題なく弾けるようにしたい!」という、
ある意味非常にプラグマティックな要求から生まれました。
その仕組みは至ってシンプル。
1オクターブを均等に12個の半音に分割するというものです。
1オクターブ上がると周波数は2倍になるのでしたね。
それを12個の同じ比率で分割するということは、隣り合う半音同士の周波数比をrとすると、r * r * r * ... (12回) ... * r = 2
つまり、r^12 = 2ということになります。
ということは、隣り合う半音の周波数比rは、2の12乗根となるわけです!
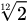
出ました!
高校数学で習った指数計算!
Excelでは^という演算子で簡単に計算できますね。
Excelワークシートを「平均律生成機」に!
これもExcelにお任せあれ!
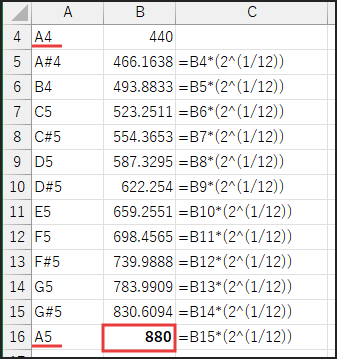
基準音A4=440HzをセルB4に入力したとしましょう。
半音上のA#(B♭)の周波数は、セルB5に=B4*(2^(1/12))と入力すれば一発です!
そのまた半音上のBの周波数は、セルB6に=B5*(2^(1/12))
これを12回繰り返せば、きっちり1オクターブ上のA5=880Hzにたどり着くはずです。
この平均律の素晴らしいところは、どの調に移っても音程の「比率」が全く変わらないため、
転調し放題という点です。
しかし、その代償として、純正律のような完全に澄み切った和音や、
ピタゴラス音律のような数学的に純粋な完全5度からは、ほんの少しずつ「ズレて」います。
全てを「そこそこ」良くするために、全てが「完璧」ではなくなる、
というある種の妥協の産物とも言えるかもしれません。
衝撃の比較!Excelが暴く音の「ズレ」の数値化:三つの音律の徹底比較!
さあ、いよいよクライマックスです!
これまで見てきた純正律、ピタゴラス音律、平均律。
それぞれが持つ「理想」と「妥協」。
これらを同じ土俵に乗せ、Excelを使ってその「ズレ」を小数点以下の具体的な数値として白日の下に晒してやりましょう!
例として、基準音をCとして、そこからの主要な音程(長3度、完全5度など)が、各音律でどのような周波数比(または周波数そのもの)になるのかを見ていきます。
そして、それぞれの音律の値を比較し、特に平均律を基準(現代音楽のデファクトスタンダードなので)として、他の音律がどれだけ「ズレている」のかを計算してみましょう。
仮にC4の周波数を261.6256 Hz(これはA4=440Hzとした場合の平均律のC4に近いです)と設定してExcelのセルに入力し、各音律のE4(長3度上)とG4(完全5度上)の周波数を計算させてみます。
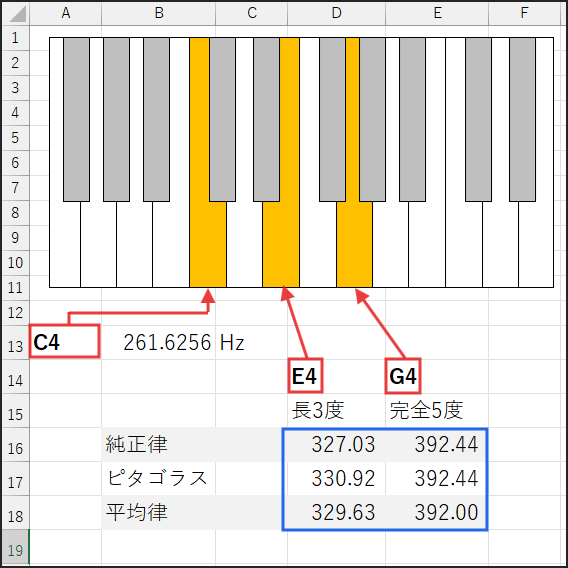
さあ、Excelの計算結果を見てください!
長3度(E4)に注目!
純正律のE4 (327.03Hz) は、平均律のE4 (329.63Hz) よりも約2.6Hz低いですね。
これが、純正律の長3度が「甘く、柔らかく」響く理由の一つです。
一方、ピタゴラス音律のE4 (330.92Hz) は、平均律よりも約1.29Hz高い!
これが、ピタゴラス音律の長3度が「硬く、時には濁って」聞こえる原因です。
完全5度(G4)に注目!
純正律とピタゴラス音律のG4 (392.44Hz) は、同じ周波数です。
しかし、平均律のG4 (392.00Hz) は、それらよりも約0.44Hz低い!
平均律の完全5度は、純正な響きからほんの少しだけ「狭く」なっているのです。
これが、平均律の和音が純正律ほど「完全に澄み切ってはいない」と感じる理由の一つ。
ほら!Excelが証明してくれました!
あなたがギターを弾いていて感じた、「気持ち悪さ」「しっくりこなさ」…
その正体の一端が、この各音律が生み出す微細な周波数の「ズレ」だったんです!
純正律の甘美な響き、ピタゴラス音律の数学的な整合性と時折見せる不協和、そして平均律のオールマイティさと引き換えのわずかな妥協。
これらが複雑に絡み合い、我々の耳に様々な印象を与えているのです。
Excelのセルに並んだこれらの数字こそ、長年の謎への明確な答え!
ギターのハーモニクスチューニングはなぜ合わないのか?Excelで徹底分析
さて、音律の基礎知識とExcelでの解析方法をゲットしたところで、いよいよ本丸!
ギタリスト長年の謎、「ハーモニクスチューニング、なんで完璧に合わないの!?」問題に、Excelを使ってメスを入れていきましょう!
あなたのその「気持ち悪さ」の正体を、今度こそ小数点以下まで特定してやりますよ!
ギターのハーモニクス音と倍音
まず基本のおさらいです。
ギターのハーモニクスポイント(例えば5フレット、7フレット、12フレットなど)で軽く弦に触れてピッキングすると、ポーンと澄んだ音が出ますよね。
あれがハーモニクス音です。
これらのハーモニクス音は、弦の基本振動(開放弦の音)に対して、整数倍の周波数を持つ「倍音」の一部を強調して取り出したものです。
- 12フレットハーモニクス: 開放弦の音の2倍音(1オクターブ上の同じ音)
- 7フレットハーモニクス: 開放弦の音の3倍音(1オクターブと完全5度上の音)
- 5フレットハーモニクス: 開放弦の音の4倍音(2オクターブ上の同じ音)
- 4フレット(正確には3.8フレット付近)ハーモニクス: 開放弦の音の5倍音(2オクターブと長3度上の音)
- 9フレットハーモニクス: 開放弦の音の3倍音(7フレットと同じ。ただし場所が違う)
ここでのポイントは、ハーモニクスで得られる音は、理論上、元の音の周波数の「きれいな整数倍」になっているということです。
これが何を意味するか…もうお分かりですね?
そう、ハーモニクスでチューニングするということは、知らず知らずのうちに「ピタゴラス音律」や「純正律」に近い音程関係を作り出そうとしている、ということなんです!
だって、3倍音(完全5度)とか5倍音(長3度)って、まさにピタゴラス音律や純正律の構成要素でしたよね?
Excelでハーモニクス周波数を「精密計算」
では、実際にExcelを使って、ギターの各弦のハーモニクス音が「理論上」どのくらいの周波数になるのかを計算してみましょう。
そのためには、まず各開放弦の周波数を正確にExcelに入力する必要があります。
ここでは、一般的なレギュラーチューニング(E-A-D-G-B-E)で、A4=440Hzを基準とした平均律の周波数を、小数点以下もなるべく忠実に入力する想定で話を進めます。
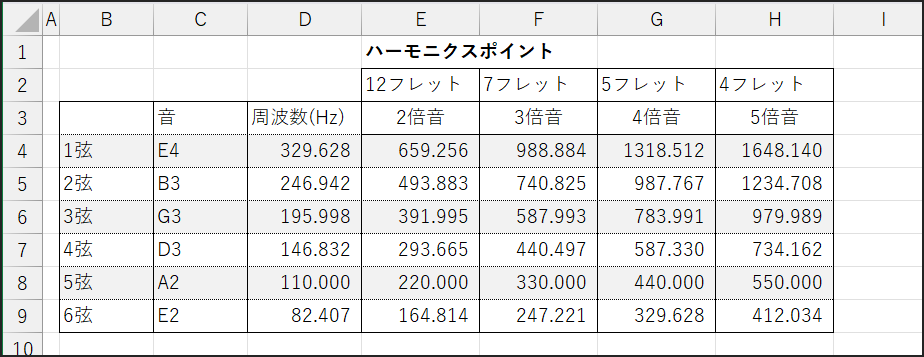
さあ、これらの開放弦の周波数を元に、Excelでハーモニクス音の理論周波数を計算していきましょう。
例えば、6弦5フレットハーモニクス(E4の音が出るはず)の周波数は、6弦(セルD9)の周波数の4倍なので、=D9*4となります。
同様に、5弦7フレットハーモニクス(E4の音が出るはず)の周波数は、5弦(仮にセルD8)の周波数の3倍なので、=D8*3です。
これを各弦、各ハーモニクスポイントについて計算させていけば、準備はOK!
音のズレを「セント」で精密測定!〜ハーモニクスチューニングの真実〜
周波数で比較してもいいのですが、音の「ズレ」をより人間の感覚に近い形で、かつ精密に表現するためには「セント(cent)」という単位を使うのが一般的です。
覚えていますか?
1オクターブは1200セント。
そして、平均律の半音は100セントです。
2つの周波数 f1 と f2 があったとき、その音程のセント値は、以下の数式で計算できます。
きたぞ、本日の主役、LOG関数の登場だ!
セント差 = 1200 * LOG(f2 / f1, 2)
この数式の意味、分かりますか?
f2 / f1は、周波数比ですね。
LOG(周波数比, 2)というのは、「2を何乗したらこの周波数比になりますか?」という問いの答え(底を2とする対数)です。
1オクターブ(周波数比2)だとLOG(2, 2) = 1になります。
それに1200を掛けているので、1オクターブなら1200セント、となるわけです。
Excelでこの計算をするには、LOG関数を使います。
例えば、セルD6にf1の周波数、セルE6にf2の周波数が入力されている場合、セント差は=1200*LOG(E6/D6, 2)
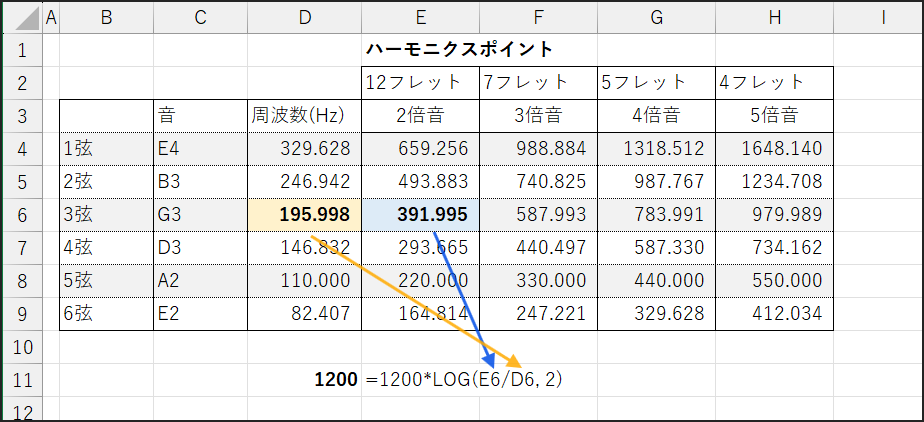
または、=1200*(LOG(E6,2)-LOG(D6,2))という形でも計算できます。
(対数の性質log(a/b) = log(a) - log(b)を利用)
ExcelのLOG関数は、デフォルトだと底が10(常用対数)なので、LOG(数値, 底)のように底を指定するのを忘れないでくださいね!
LOG(数値, 2)で底を2にできます。
いよいよ本題!ハーモニクスチューニングで最もズレるポイントはどこだ!?
お待たせしました!
いよいよExcelを使って、ハーモニクスチューニングの「気持ち悪さ」の正体を数値で暴き出します!
一般的なチューニング方法はこれですね!
- 6弦5フレットハーモニクス(理論上E4)と、5弦7フレットハーモニクス(理論上E4)を合わせる
- 5弦5フレットハーモニクス(理論上A4)と、4弦7フレットハーモニクス(理論上A4)を合わせる
- 4弦5フレットハーモニクス(理論上D5)と、3弦7フレットハーモニクス(理論上D5)を合わせる
- ここが問題! 3弦4フレットハーモニクス(理論上B4より少し低いG#5倍音)と、2弦の開放弦B3を合わせる? いや、普通は2弦の開放Bと3弦の4フレット実音Bを合わせたり、… ハーモニクスだけでBを合わせるのはちょっと難しいですね。一般的には3弦と2弦の間はハーモニクスで直接合わせにくいポイントです。
- 2弦5フレットハーモニクス(理論上B4)と、1弦7フレットハーモニクス(理論上B4)を合わせる
以下、フレットを「F」と表記する場合もあります。
では、Excelを使って、例えば「6弦5Fハーモニクス」と「5弦7Fハーモニクス」が、理論上は同じE4の音になるはずなのに、実際にはどれくらいセント値がズレているのかを計算してみましょう!
前提として、6弦E2の周波数をセルB6に82.40689 Hz、5弦A2の周波数をセルB7に110.00000 Hzと入力したとします。
計算は次の通りです。
1. 6弦5Fハーモニクスの周波数 (E4のはず):=B6*4→ これをセルB9に計算させると329.62756Hz
2. 5弦7Fハーモニクスの周波数 (E4のはず):=B7*3→ これをセルB10に計算させると330.00000Hz
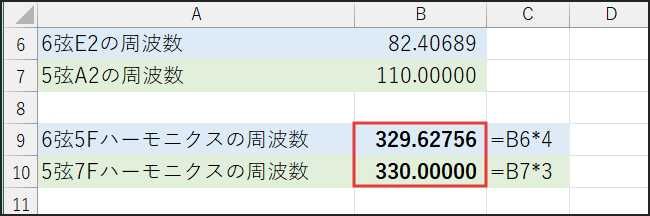
おや?
すでに周波数が微妙に違いますね!
329.62756Hz と330.00000Hz
では、この二つの音のズレをセントで計算してみましょう。
基準を6弦5Fハーモニクス(B9)とし、5弦7Fハーモニクス(B10)がどれだけズレているかを見ます。
ズレ(セント) = 1200*LOG(B10/C6, 2)
これをExcelのセルB12に計算させると…=1200*LOG(330/329.62756, 2)→ 約1.955セント
出ました!
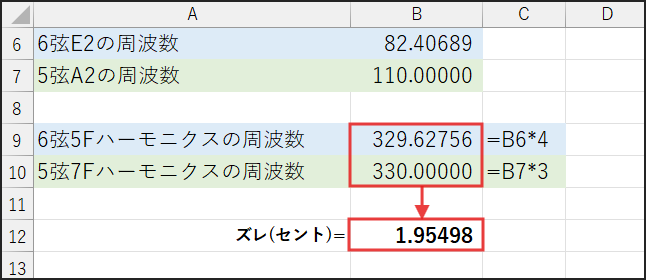
もしあなたが6弦5Fハーモニクスを基準に、5弦7Fハーモニクスをピッタリ合わせようとすると、
その5弦から派生する音は、元々の平均律の音に対して約1.96セント高くなってしまう、ということです!
1セントは半音の1/100。
2セント弱というと、耳の良い人なら「ん?ちょっと高いな?」と感じるレベルのズレです。
これが、ハーモニクスで順番に音を合わせていくと、だんだん全体の調律が狂ってくる原因の一つなんです!
6弦(開放E2)と1弦(開放E4)の音のズレをExcelで徹底解析
ギタリストが最も「気持ち悪い!」と感じやすいポイントの一つが、チューニングを終えたはずなのに、6弦のEと1弦のEの響きがしっくりこない、という現象ではないでしょうか。
特にハーモニクスチューニングを丁寧に行った(つもりの)後にこれが起きると、本当にモヤモヤしますよね。
Excelで、この謎に迫りましょう!
一般的なハーモニクスチューニングの手順をたどると、6弦 → (5F vs 5弦7F) → 5弦 → (5F vs 4弦7F) → 4弦 → (5F vs 3弦7F) → 3弦 …と、3倍音(完全5度)を頼りに音を合わせていく場面が多くなります。
これは何を意味するかというと、ピタゴラス音律の特性がチューニングに強く影響してくるということです。
ピタゴラス音律では、完全5度を12回積み重ねると、元の音の7オクターブ上にほぼ戻ってきますが、完全には一致せず、わずかに高くなります。
このズレを「ピタゴラス・コンマ」と呼び、その値は約23.46セントです。
もっと直接的に、ハーモニクスチューニングの過程で1弦のE4が、6弦のE2から見てどれだけズレてしまう可能性があるかを考えてみましょう。
仮に、6弦E2を完璧な基準とします。
1弦E4は、6弦E2のちょうど2オクターブ上の音のはずです。
つまり、セント値で言えば、6弦E2を0セントとすると、1弦E4は2400セントになるのが「平均律的には」理想です。
6弦E2 (82.40689 Hz) を基準0セントとします。
1弦E4の平均律での目標周波数は 329.62756 Hz です。
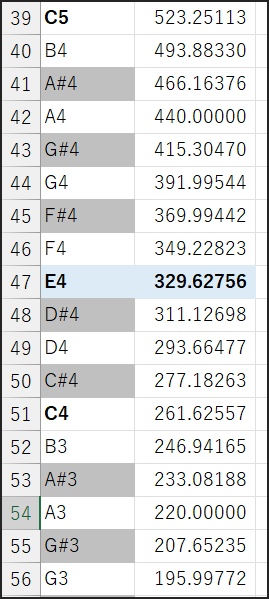
このセント値は1200*LOG(329.62756/82.40689, 2) = 2400セント (当然!)
では、ハーモニクスチューニングを繰り返した結果、1弦E4の周波数が、例えば先ほどの「3倍音の積み重ね」の影響で、平均律よりもピタゴラス音律の長3度や長6度に近い特性を帯びたと仮定してみましょう。
これは非常に簡略化した思考実験です。実際のズレはもっと複雑な要因が絡みます。
ピタゴラス音律では、2オクターブと長3度(これはE2に対するG#4に相当)は、純正律や平均律のそれよりも高くなる傾向がありました。
例えば、E2から見て、ピタゴラス的な音程の積み重ねでE4に到達したとします。
その過程で、3倍音(完全5度)が多用されるため、先述の「ピタゴラス・コンマ」のズレが蓄積し、最終的に1弦のE4が、6弦E2に対して平均律の2オクターブよりもわずかに高くなってしまう傾向があるのです。
そのズレは、数セント単位になることが多いです。
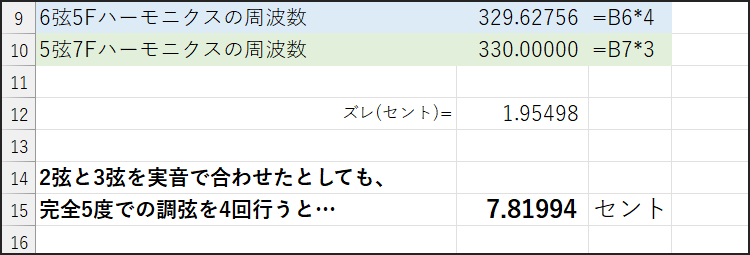
あなたの耳が感じた6弦と1弦の気持ち悪さは、Excelのセルに数字としてハッキリ刻まれました!
これは気のせいじゃなかったんです!
ハーモニクス音(特に3倍音=完全5度系列)を頼りにチューニングを進めていくと、
どうしてもピタゴラス音律的な「クセ」が乗り移り、平均律の妥協点からは少しズレてしまう。
特にオクターブ関係にある音が、その「クセ」の蓄積によって微妙にうねって聞こえてしまう。
これが、あのモヤモヤの正体だったというわけです!
じゃあどうする?〜チューナーなしで音を合わせる暇つぶし〜
さて、ハーモニクスチューニングの「気持ち悪さ」の正体が、音律の特性とExcelによる数値計算で明らかになりました。
「じゃあ、結局どうやってチューニングすりゃいいんだよ?」
という声が聞こえてきそうですね(笑)
まず大前提として、現代の音楽制作やバンド演奏においては、高精度なクロマチックチューナーを使うのが一番手軽で確実です。
これは揺るぎない事実。
プロもアマも、まずはチューナーを信じましょう!
しかし!
「この知識とExcelの計算能力を活かして、チューナーなしで、あるいはチューナーを使いつつも、もっと自分にとって『気持ちいい』調弦を追求できないものか?」
今回の「暇つぶし」のゴールは、チューナーを否定することではありません。
むしろ、Excelを使って音の構造を理解した上で、自分だけの「こだわりチューニング」を探求する遊びを提案したいのです。
Excelで「理想のチューニング周波数」を計算する
はじめに、基本に立ち返り、ギターの各弦が平均律において、どのような周波数になるのが「理論上の目標」なのかをExcelで正確に計算しておきましょう。
これは先ほども少し触れましたが、A4=440Hzを基準として、各弦の目標周波数を考えます。
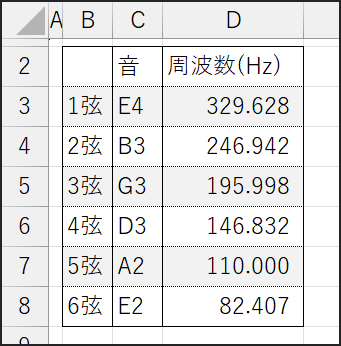
これらの周波数が、まずは我々の「基準点」となります。
市販のチューナーは、基本的にこれらの周波数に合わせようとしてくれますよね。
「ギターの特性」をExcelで考慮するヒント(マニア向け要素)
ここからが、さらにマニアックな「暇つぶし」の領域です!
実際のギターという楽器は、弦を押さえると張力がわずかに上がり、音がシャープ(高くなる)する傾向があります。
特に1~3フレットあたりを押さえた時や、チョーキングした時などは顕著ですよね。
また、コードを弾いたときの全体の響きをより美しくするために、あえて特定の弦を平均律からわずかにずらす「ストレッチチューニング」という概念も存在します。
ピアノの調律などでは一般的なテクニックですが、ギターでもこれを意識する人がいます。
「これらの微妙な物理特性や響きの好みを、Excelの数式で微調整できないだろうか?」
そう、できるんです!
これぞExcelで暇つぶしの真骨頂!
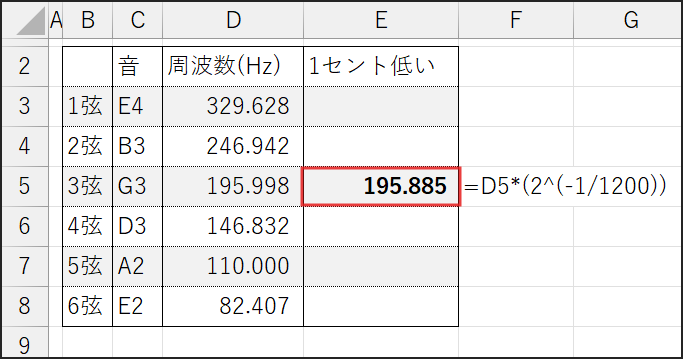
例えば、「俺のギター、3弦を押さえるといつも2セントくらいシャープするんだよな…。だから、開放弦をあらかじめ1セントくらい低めにチューニングしておこうかな」なんていう調整をExcelで計算できます。
目標周波数がセルD5(G3)に入っているとして、これを1セント低くしたい場合、新しい目標周波数 =元の周波数 * (2^(-1/1200))という計算式になります。
Excelのセルには、=D5*(2^(-1/1200))と入力すればOK!
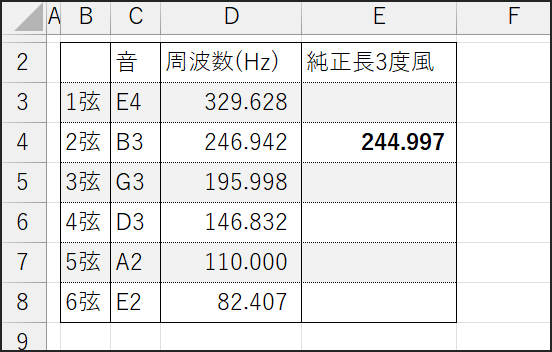
あるいは、特定の弦の倍音構成を考慮して、純正律の響きに近づけるために、平均律から意図的に数セントずらす、なんていう実験も面白いかもしれません。
例えば、「GとBの長3度の響きを、もっと純正律っぽく甘くしたいから、B弦を平均律より14セントくらい低めにしてみようかな?」といった感じです。
純正律の長3度は平均律の長3度より約13.69セント低い
B弦の目標周波数(平均律) = 246.9412 Hz(セルD4)
B弦の目標周波数(純正長3度風) = D4 * (2^(-13.69/1200)) →244.99... Hz
このように、Excelの数式一つで、あなたの「こだわり」をチューニングの目標値に反映させることができるのです!
これはもう、自分だけのカスタム音律ジェネレーターを作っているようなものですね!
この「ギター × Excel」暇つぶしがあなたに与えるもの
さて、ここまでギターのチューニングの謎をExcelで解き明かすという、「暇つぶし」にお付き合いいただき、ありがとうございました!
この一見風変わりな探求が、あなたに何かしらの新しい発見や面白さを提供できたとしたら、これほど嬉しいことはありません。
今回の「暇つぶし」は、単なるギターの調弦テクニックの紹介ではありませんでした。
それは…
- 音楽の「科学」への探求心: 普段何気なく聞いている音楽や楽器の音が、実は厳密な物理法則と数学的関係性の上に成り立っているという事実。その一端をExcelというツールで垣間見る体験。
- 複雑な概念の「見える化」能力: 音律やセントといった、言葉だけでは捉えにくい複雑な音の概念を、Excelの数値計算や(もしグラフを使えば)グラフ化によって、具体的かつ客観的に「見える化」するスキルの獲得。
- 「比」と「対数」を操る快感: 周波数比が音程を決定し、その感覚が対数的であるという本質を理解し、「比」や「セント」といった単位をExcelのLOG関数や
^演算子を駆使して自在に操るテクニカルな面白さ。 - 数学と音楽の美しい連携の発見: 数学的な思考や計算が、音楽の理解を深め、さらには演奏の質を向上させる可能性を秘めているという発見。
そして何よりも、Excelが持つ「計算」と「可視化」、そして「未知なるものを探求する道具」としての無限の可能性を、改めて感じていただけたのではないでしょうか。
これこそが、「l暇つぶし」の真髄なのです!
この経験は、直接的にあなたのギタープレイを飛躍的に向上させるものではないかもしれません。
しかし、あなたがギターの音、音楽の構造に対して、より深く、より知的な興味を持つきっかけになったとしたら、それは素晴らしいことです。
そして、Excelというツールを見る目が、少し変わったかもしれませんね!
まとめ:ギターは「数学」と「Excel」で覚醒する
なかなかの長旅でしたね!
「今度、自分のギターの開放弦の周波数を正確に調べて、Excelで理想のチューニング表を作ってみようかな…」なんて少しでも思ってくれたなら、この「暇つぶし」は大成功です!
ぜひ一度、あなたのお手元のExcelを起動して、今日ご紹介したような計算を試してみてください。
電卓を叩くように数値を入力し、数式を組み立て、その結果がセルに表示された瞬間… きっと、「おおっ!」「なるほど!」といった小さな感動と「発見」があるはずです。
それは、あなたのギターの音が、そして音楽そのものが、よりクリアに、より深く理解できた証。
あなたのギターは、もしかしたら「数学」と「Excel」という新たな視点によって、今までとは違う響きで「覚醒」するかもしれませんよ?
さあ、Excelという万能ツールは、あなたの知的好奇心と探求心を満たすために、いつでもスタンバイしています。
あなたの次なる「Excel暇つぶし」は何ですか?
この音の謎、あなたはExcelでどこまで解き明かせましたか?
最後までお読みいただき、本当にありがとうございました!




