まず、Excelで暇つぶし、Excelでアート、してますか?
以前、単純な格子模様をExcelで描いてみる記事をご紹介しました。(まだの方はぜひ!)
格子模様を作成!100×100マスを塗りつぶす方法
あれもなかなかの暇つぶしになりました!
「Excelでアート?しかも数式で?そんなバカな!」
Excelのポテンシャルをまだまだ見くびってはいけません!
さて、今回はさらにステップアップします!
Excelの「数式」の力をフル活用します。
そして、もっと複雑で、もっと美しい「モザイク模様」作りに挑戦しましょう。
そう、あの小さなセルの一つ一つを「ピクセル」に見立てるのです。
次に、数式と「条件付き書式」という魔法を組み合わせるだけです。
すると、まるでプログラムで描いたような、驚きの幾何学模様がExcelシート上に現れます!
「Excelってこんな表現もできるんだ!」という発見があります。
また、「この関数、こんな動きするの!?」という発見の喜びもあります。
そして、数式が生み出す意外な美しさは、最高の「暇つぶし」になること間違いなしです!
さあ、あなたもExcel関数の奥深い世界を覗いてみませんか?
モザイク描画の基本ルール:シートをアートキャンバスに変える準備
本記事では、Excel 2021を使用して検証および画像の作成を行っています。
はじめに、本格的な模様作りの前に、まずは下準備から始めましょう!
Excelシートを私たちだけのアートキャンバスに変えるための、3つの簡単なステップをご紹介します。
セルを正方形に!
セルの形状調整
まず、美しいモザイク模様のためには、セルの形が重要です。
デフォルトのExcelセルは縦長の長方形ですね。
これを正方形に近づけることで、模様が歪まず綺麗に見えます。
意図した通りの美しい形で表示されるようになります。
適用範囲と設定例
次に、今回は描画範囲をA1セルからKN300セル(つまり300行 × 300列の範囲)とします。
この範囲の行の高さと列の幅を調整しましょう。
できるだけ正方形になるようにしてください。
例えば、列幅を「2.5」、行の高さを「18.75」くらいに設定します。

そうすると、だいたい正方形っぽくなりますよ。
お使いの環境やフォントによって微調整してくださいね!
「座標」を意識する!ROW()とCOLUMN()関数
それぞれの関数の詳細な仕様については、Microsoft公式のヘルプも参考にしてください。
座標の重要性
まず、数式で模様を描く上で、各セルがシート上の「どこにあるのか」が重要です。
この位置情報(座標)が超重要になります。
ここで活躍するのが、おなじみ ROW() 関数と COLUMN() 関数です!
関数の基本動作
- ROW(): そのセルが何行目にあるかを返します。
- COLUMN(): そのセルが何列目にあるかを返します。
これらの関数が、私たちの数式アートの出発点です。
各セルのX座標、Y座標のようなものだと考えてください。
例えば、B2セルなら ROW() は 2 を返します。
COLUMN() も 2 を返します(A列が1列目なので)。
座標計算の基準
続いて、今回は300×300の範囲を想定します。
多くの場合、シートの中心あたり、例えば (列:150, 行:150) を考えます。
ここを座標の「原点 (0,0)」のように見立てて計算を進めていきます。
つまり、COLUMN()-150 や ROW()-150 といった形がよく登場しますよ!
数値が色に変わる魔法!条件付き書式「カラースケール」
数値から色彩へ
まず、各セルに数式を入力すると、計算結果として「数値」が得られます。
でも、欲しいのは模様、つまり「色」ですよね?
ここで登場するのが「条件付き書式」です。
中でも特に便利な「カラースケール」機能を使います!
カラースケールの仕組み
これは、セルの数値の大小に応じて色を自動的に塗ってくれる優れものです。
グラデーションで塗ってくれます。
例えば、「最小値を赤、最大値を青」のように設定します。
そうすれば、数式の結果が小さいセルは赤っぽくなります。
大きいセルは青っぽく、その中間はグラデーションで彩られます。

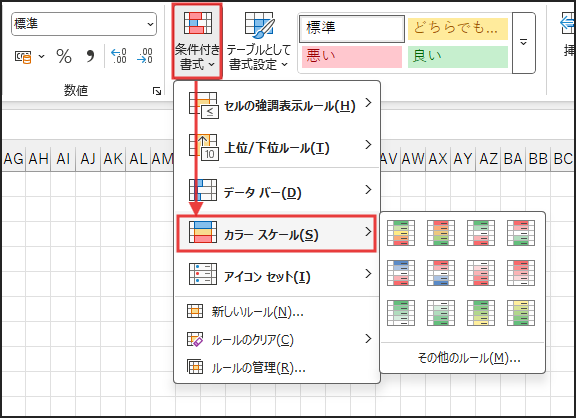
設定手順
次に、設定は簡単です!
- 描画範囲(A1:KN300)を選択します。
- 「ホーム」タブの「条件付き書式」から「カラースケール」を選びます。
- お好みの配色パターン(例:赤-黄-緑 や 青-白-赤など)を選択します。
たったこれだけで、数式が生み出す数値が美しい色彩のモザイク模様へと変わるんです!
今回は、この「カラースケール」を前提に模様を作っていきます。
そのため、複雑な条件付き書式のルール設定は不要です。
楽ちんですね!
パターン1:MOD関数で繰り返す!シンプルなブロック&ストライプ
考え方
最初にご紹介するのは、Excel関数の中でも特に「周期性」を扱うのが得意な関数です。
MOD 関数を使ったパターンです。
MOD(数値, 除数) は、「数値を除数で割った余り」を返しますよね。
この「余り」が一定のサイクルで繰り返される性質を利用します。
そして、シンプルなブロック模様やストライプ模様を作り出しましょう。
数式
まず、A1セルに以下の数式を入力してください。
次に、A1:KN300の範囲にコピーしてください。
=MOD(ROUNDUP(ROW()/2,0),2)+MOD(ROUNDUP(COLUMN()/2,0),2)
数式解説
数式の分解
なんだかゴチャっとして見えますが、分解すれば簡単です!
ROW()/2やCOLUMN()/2: 各セルの行番号や列番号を2で割っています。- ROUNDUP(…,0): 上記の結果を小数点以下切り上げで整数にしています。
- 例えば、
ROUNDUP(ROW()/2,0)の部分だけを見ると、1行目と2行目は「1」になります。 - 3行目と4行目は「2」、5行目と6行目は「3」…というようになります。
- 2行ずつのグループができます。
- 例えば、
- MOD(…,2): そのグループ番号をさらに2で割った余りを求めています。
- 先ほどの例で言うと、グループ「1」は余り「1」です。
- グループ「2」は余り「0」、グループ「3」は余り「1」…となります。
- 結果が0か1で周期的に変化します。
- 「
+」: 行方向の周期的な値と、列方向の周期的な値を足し合わせています。
模様の形成
このようにして、行ごと、列ごとに2セル単位で計算結果が周期的に変わります。
それらが組み合わさることで、市松模様のようなパターンが現れます。
あるいは太めのストライプが交差したようなブロックパターンにもなります。
そして、カラースケールによって、計算結果の0、1、2が異なる色で塗り分けられます。
最後に、シンプルな数式とは思えない模様が浮かび上がりますよ!

パターン2:SQRTとSUMSQで「距離」を測る!同心円と放射模様
考え方
次に挑戦するのは、なんだか数学っぽい響きの「距離」を使った模様です。
各セルが、シートの中心点からどれだけ離れているかを計算します。
今回は仮に(150,150)とします。
その「距離」に応じてカラースケールで色を変えればどうなるでしょう?
そう、まるで水面に石を投げたときに広がる波紋のようです。
同心円状の美しいグラデーション模様が描けるはずです!
ここで使うのは、二乗和を計算する SUMSQ 関数です。
そして、平方根を計算する SQRT 関数です。
ピタゴラスの定理を思い出しますね!
数式
まず、A1セルに以下の数式を入力してください。
次に、A1:KN300の範囲にコピーしてください。
=SQRT(SUMSQ(COLUMN()-150, ROW()-150))
数式解説
距離計算の仕組み
この数式は、まさに「中心からの距離」を計算しています。
COLUMN()-150: 列番号から150を引くことで、150列目を中心(0)とした相対的な横位置を計算します。ROW()-150: 同様に、行番号から150を引くことで、150行目を中心(0)とした相対的な縦位置を計算します。- SUMSQ(数値1, 数値2): 指定された数値の二乗の合計を返します。
- ここでは、
(COLUMN()-150)2 +(ROW()-150)2 を計算していることになります。 - これは、中心からの距離の「二乗」ですね。
- SQRT(数値): 指定された数値の正の平方根を返します。
- つまり、先ほどの二乗和の平方根を取ります。
- これにより、純粋な「中心からの距離」が算出されます。
模様の視覚化
続いて、図でイメージすると、各セル(x, y)に対して計算します。
中心を(150,150)としたときの \sqrt{(x-150)^2 + (y-150)^2} を計算しているわけです。
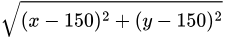
この距離が小さい(中心に近い)セルほど計算結果の数値は小さくなります。
大きい(中心から遠い)セルほど数値は大きくなります。
これをカラースケールで表示すると、中心から外側に向かって色が滑らかに変化します。
そして、美しい同心円模様や、見方によっては放射状の模様が浮かび上がるのです!

パターン3:三角関数で波を打つ!美しいグラデーション模様
考え方
数学の授業で出会った、あのサイン・コサイン・タンジェント…!
そう、三角関数の登場です!
「うっ…三角関数は苦手だった…」
大丈夫!
難しい理論は抜きにして、三角関数が持つ「波の性質」だけを拝借しましょう。
SIN 関数などは、入力値に応じて周期的に-1から1の間の値を返しますよね。
この滑らかな値の変化を利用すれば、波打つような模様が作れます。
あるいは斜めに流れるような美しいグラデーション模様が作れるんです。
数式
まず、A1セルに以下の数式を入力してください。
次に、A1:KN300の範囲にコピーしてください。
=SIN((ROW()-1+COLUMN()-1)*PI()/10)
数式解説
入力値の生成
ROW()-1+COLUMN()-1: ここでは、A1セルを基準(0+0=0)としています。- 各セルの行番号と列番号(それぞれ1を引いて0からのスタートに調整)を足し合わせています。
- これにより、セルの位置によって連続的に変化する値が得られます。
- 例えば、A1セルでは0、B1セルでは1、A2セルでは1、B2セルでは2…といった具合です。
波の調整と出力
*PI()/10: 上記の値に PI() (円周率πですね!) を掛けて10で割っています。- これは、SIN 関数に入れる角度のようなものです。
- この値を調整することで波の密度(細かさ)を変えることができます。
/10の数字を小さくすれば波は緩やかになります。- 大きくすれば波は細かくなります。
- SIN(…): そして、この計算結果を SIN 関数に入れます。
- 結果として、各セルの値は-1から1の間で滑らかに変化する数値となります。
模様の多様性
この-1から1までの連続的な数値がカラースケールによって色付けされます。
すると、まるでオーロラのような模様がシートいっぱいに広がります。
さらに、ROW()-1+COLUMN()-1 の部分を色々変えてみてください。
例えば ROW()*COLUMN() や ROW()-COLUMN() などです。
そうするだけでも、全く異なる表情の波模様が生まれます。
ぜひ実験してみてください!

パターン4:複素関数で空間を歪める!「魔法の鏡」模様
考え方
複素数の導入
さあ、ここからは少しマニアックな領域へ足を踏み入れますよ!
登場するのは「複素数(ふくそすう)」です。
覚えてますか?
a + bi ってやつです!
Excelには、この複素数を扱える関数群がちゃんと用意されているんです。
COMPLEX, IMPOWER, IMREAL, IMAGINARYなど
これを使わない手はありません!
複素関数による歪み
まず、各セルの座標 (COLUMN()-150, ROW()-150) を考えます。
これを一つの複素数 z = (x-150) + (y-150)i と見立てます。
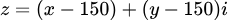
そして、この複素数に対して、例えば z^2 (zの2乗) のような単純な複素関数を適用してみるのです。
すると、あら不思議!
まるで空間がぐにゃりと歪んだような模様が現れます。
万華鏡を覗いたような、ユニークで美しい模様です。
数式
はじめに、A1セルに以下の数式を入力してください。
次に、A1:KN300の範囲にコピーしてください。
=IMAGINARY(IMPOWER(COMPLEX(COLUMN()-150, ROW()-150), 2))
数式解説
関数の役割
- COMPLEX(
COLUMN()-150,ROW()-150): これがキモです! - 各セルの相対座標 (
COLUMN()-150を実部、ROW()-150を虚部として) を複素数に変換します。 - 例えば、中心点(150,150)は 0+0i になります。
- IMPOWER(…, 2):
IMPOWER(複素数, 指数)は、複素数のべき乗を計算します。 - ここでは、先ほど作った複素数を単純に「2乗」しています。
- 複素数の2乗は (x+yi)^2 = (x^2 – y^2) + (2xy)i となります。
- 元の座標が複雑に混ざり合うのがポイントです。
- IMAGINARY(…):
IMAGINARY(複素数)は、複素数の虚部を取り出します。 - ここでは、z^2 の計算結果の虚部の値がセルの数値となります。
- (ちなみに IMREAL を使うと実部が取り出せ、また違った模様になりますよ!)
模様の生成と拡張性
このようにして、虚部の値が、カラースケールによって色に変換されるわけです。
たったこれだけの処理で、中心から放射状に広がりつつ回転するような模様が生まれます。
非常に面白いパターンです。

さらに、IMPOWER の指数を 2 から 3 や 1.5 などに変えてみてください。
そうすると、歪み方が変わってさらに楽しめます!

パターン5:波の交差点!予測不能な異世界模様
導入
さて、みなさん…。
ここからは、ちょっと覚悟してください。
今までのパターンは、いわば序の口、前菜のようなものでした。
これからお見せするのは、これまで紹介した様々な関数をこれでもかと組み合わせます。
Excelに「予測不能な絵」を描かせるのです。
まさに究極の暇つぶしアートです!
「え、Excelが暴走するの…?」
ご安心を(?)。
ちゃんと数式に支配された、秩序ある混沌(カオス)が生まれますから!
考え方
基本方針:三角関数の重ね合わせと角度変調
まず、このパターンの核心は、多数のSIN関数とCOS関数、そしてATAN2関数を駆使することにあります。
各セルの座標 (COLUMN()-150, ROW()-150) を基準とします。
これにより、300×300セルのキャンバスの中心が原点(0,0)のように扱われます。
次に、これらの座標値を異なる係数で割って複数のSIN波とCOS波を生成し、それらを掛け合わせます。
この操作により、非常に複雑な周波数を持つ波の干渉模様を作り出します。
ATAN2による角度の導入とさらなる変調
続いて、ATAN2関数を使って、これらの干渉波から角度情報を抽出します。
ATAN2関数は、原点から指定した(x,y)座標への角度を返すため、模様に回転や渦のような要素を加えることができます。
さらに、この角度情報に別のSIN波とCOS波の組み合わせを加えて変調し、予測不能性を高めます。
最終的な量子化による模様の確定
そして最後に、複雑に変調された波の値を大きな係数で増幅し、INT関数で整数に丸めます。
この「量子化」の処理によって、滑らかなグラデーションではなく、色の境界が明確な、
まるで細胞や地形図、あるいは抽象画のような複雑怪奇なパターンが浮かび上がります。
まさに、数式が生み出す「秩序ある混沌」と言えるでしょう。
数式
心してA1セルに以下の数式を入力してください!
そして、A1:KN300の範囲(300行x300列)にコピーしてください!
=INT(SIN(DEGREES(ATAN2(COS((COLUMN()-150)/10)*SIN((ROW()-150)/100),SIN((COLUMN()-150)/50)*COS((ROW()-150)/20)))*PI()/180+COS((COLUMN()-150)/30)*SIN((ROW()-150)/40)/20)*300)
数式解説
ステップごとの解説
もはや呪文に見えるかもしれませんが、じっくりと分解していきましょう!
座標の基準化と初期波形の生成
まず、COLUMN()-150 と ROW()-150 の部分です。
これらは、300×300セルの描画範囲の中心を(0,0)とするための座標変換です。
次に、これらの相対座標を異なる数値(10, 100, 50, 20など)で割って、
COS関数やSIN関数に入れています。
例えば COS((COLUMN()-150)/10) や SIN((ROW()-150)/100) といった部分です。
これにより、座標位置に応じて周期的に変化する複数の基本的な波形が作られます。
割る数値が小さいほど波は細かく、大きいほど緩やかになります。
ATAN2による角度の複雑な生成
続いて、ATAN2(y, x) 関数の部分です。
この関数は、原点から点(x,y)への角度をラジアン単位で返します。
ここでは、y引数に COS((COLUMN()-150)/10)*SIN((ROW()-150)/100) を、
x引数に SIN((COLUMN()-150)/50)*COS((ROW()-150)/20) を指定しています。
つまり、2つの複雑な波の干渉パターンをx成分とy成分として、それらが合成された結果としての「角度」を各セルに対して計算しているのです。
これにより、非常に変化に富んだ角度の場が生成されます。
角度の再変換とさらなる変調
次に、DEGREES(ATAN2(...)) * PI() / 180 の部分です。
ATAN2が返したラジアン単位の角度を、DEGREES関数で一度「度」に変換し、それを即座に * PI() / 180 で再び「ラジアン」に戻しています。
これは実質的に元のラジアン角のままですが、数式にこのようなステップを挟むことで意図的な複雑さを加えています。(無駄なことをしています!)
さらに、この角度に対して + COS((COLUMN()-150)/30)*SIN((ROW()-150)/40)/20 という別の波の干渉結果を加算しています。
これにより、角度はさらに複雑に変調されます。
最終的な波形の生成と量子化
そして、この複雑に加工された角度を、外側の SIN 関数 SIN(...) に入力します。
これにより、-1から1の間で振動する最終的な波形が得られます。
この結果に * 300 を乗じて振幅を-300から300に拡大します。
最後に、INT 関数でこの値を整数に丸めます。
この整数化によって、滑らかな色の変化ではなく、色の境界が明確に区切られた、予測不能で有機的なパターンが完成するのです!
パラメータ変更の妙
この数式の面白さは、各パラメータ(COSやSINの中の除数、ATAN2の引数の組み合わせ、最後の乗数など)をほんの少し変えるだけで、模様が劇的に変化する点です。
どんな模様が出るかは、実際に試してみてのお楽しみです。
ぜひ、これらの数値を色々変更して、あなただけの「予測不能な異世界」をExcel上に創り出してみてください!

この「Excelアート」暇つぶしがあなたに与えるもの
さて、5つの驚きのモザイク模様、楽しんでいただけましたか?
「こんなの作って何になるの?」
この一見「無駄」とも思えるExcelアートへの挑戦は、きっとあなたに新しい発見とスキルをもたらしてくれたはずです。
- Excelのセルが、単なる表計算のマス目ではないということ
- 創造力を刺激するアートキャンバスになり得るという発見
- MOD, SQRT, SIN, そして複素関数といった関数
- 条件付き書式「カラースケール」と数式の連携
- どこまでも「遊ぶ」ことができるという無限の可能性!
そうです、これは最高の知的な暇つぶしです。
まとめ:Excelは、ただの「表計算ソフト」ではない
今回は、Excelの数式と条件付き書式だけで描く「モザイク模様」をお届けしました。
ぜひ、今日紹介した数式をコピー&ペーストして遊んでみてください。
もちろんそれだけでなく、あなた自身の手で数値をいじったりしてみてください。
きっと、時間を忘れて没頭してしまうはずです。
(気づけば関数のスキルも少しアップしているかもしれません!)
それでは、また次回の暇つぶしでお会いしましょう!