Excelでランダム?確率?
日常で「ランダム」という言葉を使うとき、多くの人が思い浮かべるのは、サイコロ投げではないでしょうか。
サイコロは、その手軽さからゲームや運試しなど、様々な場面で「公平な結果」を期待して使われます。
では、私たちの身近なツールであるExcelを使ってサイコロを振ったとしたら、それは本当に公平な結果をもたらすのでしょうか?
その結果が私たちの期待する「公平さ」とどれだけ一致するのか、
あるいは「偏る」のかを観察していきます。
本記事では、Excel 2021を使用して検証および数式の作成を行っています。
真剣に追求する「どうでもいいこと」
まず、「Excelでサイコロを振って、その公平性を確かめるなんて、なんだかどうでもいいことじゃない?」
――そう思われるかもしれません。
しかし、一見すると些細な疑問や「どうでもいいこと」に真剣に取り組むと、思わぬ発見や学びがあるものです。
そして何より、その探求の過程自体が面白いのです。
この記事では、そんな「真剣な暇つぶし」の精神で、Excelの乱数機能を使ってサイコロを振るシミュレーションを行います。
ExcelのRAND関数で乱数の「偏り」があるかどうか
Excelには RAND という関数があり、これを使うと0以上1未満の乱数(ランダムな数値)を簡単に生成できます。
次に、この関数を少し加工すれば、サイコロの1から6までの目をシミュレーションすることが可能です。
しかし、ここで素朴な疑問が湧いてきます。
「このExcelサイコロは、本当にそれぞれの目を公平に出してくれるのだろうか?」
「もしかしたら、少ない回数試しただけでも、すでに何らかの偏りが現れているのではないだろうか?」
そこで今回は、Excelの関数(特に RAND 関数)の基本を学びつつ、さらに強力な助っ人であるVBA(Visual Basic for Applications)を駆使して、大量のサイコロ振りシミュレーションを実行します。
そして、RAND 関数(正確にはVBA内でサイコロの目を生成する際の乱数)が示すかもしれない「小さな偏り」を、皆さんと一緒に目撃していく「暇つぶし統計分析」に挑戦します。
果たして、Excelのサイコロは私たちの期待に応えてくれるのでしょうか?
STEP1:Excel関数でサイコロを「振る」!基本と「確率」のおさらい
シミュレーションを始める前に、まずは「公平なサイコロ」とは何か、
そしてExcelの RAND 関数をどのように使えばサイコロの目を表現できるのか、基本を確認しておきましょう。
公平なサイコロが持つ「期待」、RAND関数の加工
サイコロと言えば、1から6までの目が描かれた立方体です。
ここでは、それぞれの目がどれくらいの確率で出るのか、そしてそれをExcelでどう表現するのかを見ていきます。
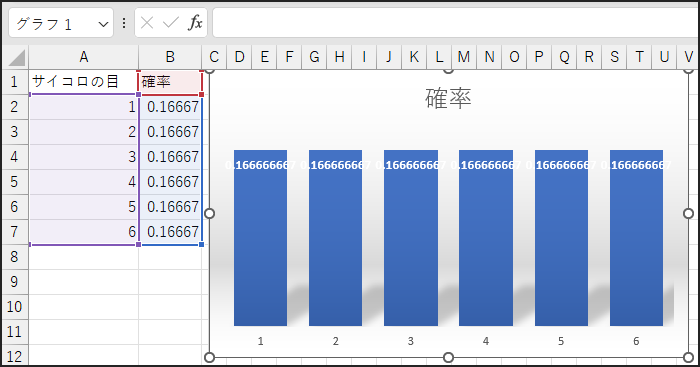
サイコロの目と確率の基本
もし手元にあるサイコロが完全に公平(いかさまではない、完璧な形をしている)ならば、
1の目が出る確率、2の目が出る確率、…、6の目が出る確率は、すべて等しく 1/6 (約16.7%)になるはずです。
これは、サイコロを1回振ったときに、それぞれの目が現れることへの「期待度」とも言えます。
続いて、統計の世界には「大数の法則」という考え方があります。
これはざっくり言うと、
「試行回数を増やせば増やすほど、実際に観測される結果の平均値は、理論上の期待値(真の確率)に近づいていく」
というものです。
今回のシミュレーションでは、この「大数の法則」のほんの小さな片鱗を垣間見ることを目指します。
つまり、サイコロを振る回数を増やしていくと、各目の出現割合が 1/6 に近づいていくのかどうかを観察するのです。
RAND() 関数の基本とサイコロの目への加工方法
Excelで乱数を扱う基本的な関数が RAND() です。
この関数は、引数を必要とせず、セルに =RAND() と入力するだけで、
0以上1未満の小数点以下の数値をランダムに返します。
例えば、0.12345 や 0.87654 といった具合です。
しかし、このままではサイコロの目としては使えません。
そこで、この RAND() 関数の結果を加工して、
サイコロの目である1から6までの整数を作り出す「加工」が必要になります。
その数式は以下の通りです。
=INT(RAND()*6)+1この数式がどのようにして1から6までの整数を生成するのか、ステップごとに見ていきましょう。
RAND(): まず、RAND()が0以上1未満の乱数を生成します。(例:0.0から0.999...の範囲)RAND()*6: 次に、その結果を6倍します。すると、範囲は0以上6未満の数値になります。(例:0.0から5.999...の範囲)INT(RAND()*6):INT関数は、小数点以下を切り捨てて整数にする関数です。これにより、範囲は0, 1, 2, 3, 4, 5のいずれかの整数になります。INT(RAND()*6)+1: 最後に、その結果に1を加えます。これで、範囲は1, 2, 3, 4, 5, 6のいずれかの整数となり、サイコロの目として使える数値が得られるわけです。
まずは手動で試してみよう!
実際にExcelの任意のセルに =INT(RAND()*6)+1 と入力してみてください。
Enter キーを押すと、1から6までのいずれかの数値が表示されるはずです。
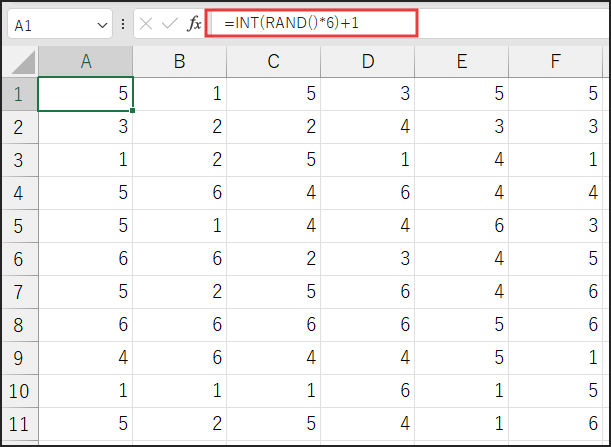
さらに、そのセルを選択した状態で F9 キーを押すと、
Excelが再計算を行い、セルの数値がランダムに変化するのが確認できます。
これを10回、20回と手動で繰り返してみると、
結果がバラバラで「いかにもランダムに見える」ことでしょう。
しかし、この時点ではまだ、それぞれの目が公平に出ているのか、
それとも何らかの「偏り」があるのかは、なかなかわかりにくいものです。
STEP2:VBA導入!サイコロを「自動」で振るツールを作ろう!
手動で F9 キーを何度も押して結果を記録するのは、
数回ならまだしも、何百回、何千回となると現実的ではありません。
そこで登場するのがVBAです。
VBAを使えば、このサイコロ振り作業を自動化し、
大量の試行を効率的に行うことができます。
手動では非効率!VBAで「自動化」
はじめに、
「サイコロを100回振って、それぞれの目が何回出たか記録する」
という作業を考えてみてください。
手作業では時間がかかり、入力ミスも起こり得ます。
しかし、VBAマクロを使えば、このような反復作業を、正確かつ高速に実行させることが可能です。
今回は、VBAを使って「指定した回数だけサイコロを振り、その結果をExcelシートに自動で書き出す」
という、シンプルな「自動化ツール」を作成します。
VBAコードの作成とマクロ実行ボタンの設置
VBAコードは「標準モジュール」という場所に記述するのが一般的です。
ここでは、その手順を解説します。
VBA実行環境の準備
開発タブの表示: まず、Excelのリボンに「開発」タブが表示されていない場合は、これを表示させる必要があります。
「ファイル」タブから「オプション」を選び、「リボンのユーザー設定」を開きます。そして、右側の「メインタブ」一覧にある「開発」にチェックを入れてOKします。
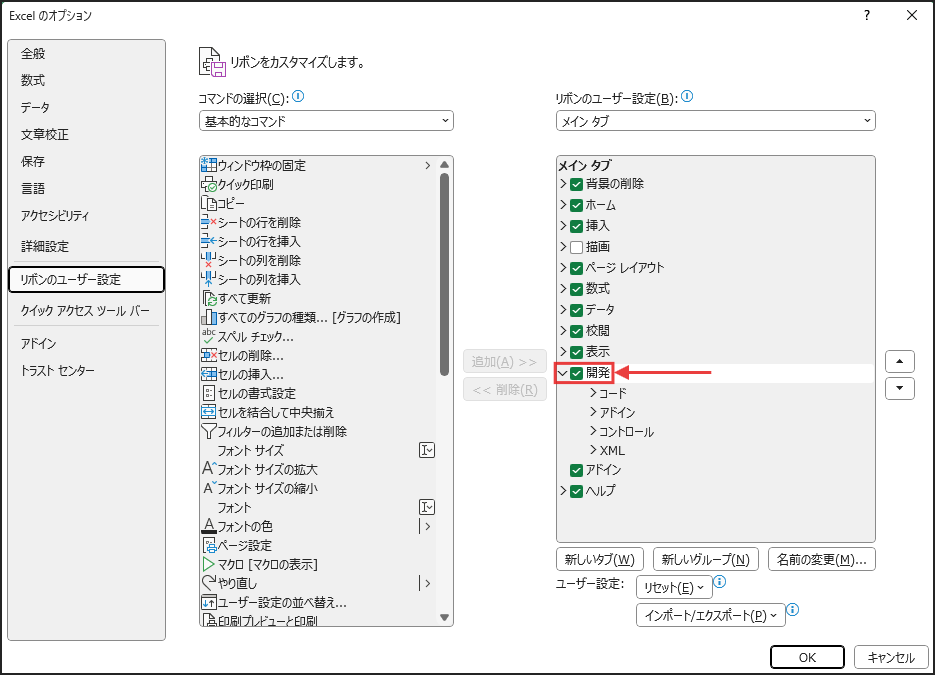
VBAエディタを開く: 次に、「開発」タブの左端にある「Visual Basic」ボタンをクリックすると、VBAエディタ(VBE)が開きます。

標準モジュールを挿入: VBEのメニューから「挿入」を選び、「標準モジュール」を選択します。
すると、プロジェクトエクスプローラーウィンドウに新しい「Module1」などが表示され、
右側にコードを記述する白いウィンドウが現れます。
VBAコードの記述と解説
コードの貼り付け: 以下のVBAコードを、表示されたコードウィンドウにコピーアンドペーストします。
Sub RollDice_100回()
Const NumRolls As Long = 100 ' ★★★ 試行回数を設定 ★★★
Dim ws As Worksheet
Dim i As Long
' ★★★ 結果を出力するシート名に合わせてください ★★★
On Error Resume Next ' シートが存在しない場合のエラーを無視
Set ws = ThisWorkbook.Sheets("100回")
If ws Is Nothing Then
MsgBox "シート「100回」が見つかりません。", vbExclamation
Exit Sub
End If
On Error GoTo 0 ' エラーハンドリングを元に戻す
ws.Cells.ClearContents ' シートの内容をクリア
ws.Range("A1").Value = "サイコロ振りシミュレーション結果 (VBA: Rnd)"
ws.Range("A2").Value = "試行回数:" & NumRolls & "回"
ws.Range("A4").Value = "出目" ' 見出し
Application.ScreenUpdating = False ' 画面描画を一時停止 (高速化のため)
Application.Calculation = xlCalculationManual ' 計算モードを一時的に手動に (高速化のため)
' サイコロを振り、結果をA列に書き出す
For i = 1 To NumRolls
' VBAのRnd関数を使ってサイコロの目を生成 (1から6の整数)
ws.Cells(i + 4, 1).Value = Int(Rnd() * 6) + 1
Next i
Application.Calculation = xlCalculationAutomatic ' 計算モードを自動に戻す
Application.ScreenUpdating = True ' 画面描画を再開
MsgBox NumRolls & "回のサイコロ振りシミュレーションが完了しました!", vbInformation
End Sub
このコードは、RollDice_100回 という名前のマクロです。
これは、「100回」という名前のシートに100回サイコロを振った結果(1から6のいずれかの数値)を A5 セルから順に書き出します。
NumRolls という定数の値を変更し、
Set ws = ThisWorkbook.Sheets("シート名")
のシート名を対象のものに変更すれば、
異なる回数や異なるシートへの出力を簡単に行うことができます。
例えば、1000回振りたい場合は
Const NumRolls As Long = 1000
とし、出力先シートも「1000回」シートに変更するといった具合です。
マクロ実行ボタンのシートへの設置
作成したマクロは、Excelシート上に配置したボタンから簡単に実行できるようにすると便利です。
まず、Excelシートに戻り、「開発」タブの「コントロール」グループにある「挿入」をクリックします。

次に、「フォームコントロール」の中から「ボタン(フォームコントロール)」を選択します。
続いて、シート上でボタンを配置したい場所をドラッグしてボタンを作成します。
「マクロの登録」ダイアログボックスが表示されたら、先ほど作成した RollDice_100回 を選択し、「OK」をクリックします。
最後に、ボタンのテキストを「100回振る」などに変更すれば完成です。
これで、ボタンをクリックするだけで指定回数のサイコロ振りシミュレーションが実行できるようになりました。
STEP3:サイコロを「1万回」振る!偏りを見つけて、大数の法則を体感しよう!
いよいよ、VBAを使って大量のサイコロ振りシミュレーションを実行し、その結果を分析していきます。
試行回数を増やすことで、乱数が持つ真の姿、
そして「大数の法則」がどのように現れるのか(あるいは現れないのか)を観察しましょう。
ここでは、試行回数を100回、1,000回、10,000回と増やしていくことで、
結果がどのように変化するのかを比較します。
準備:コントロールシートと結果シートの作成
シミュレーションをスムーズに行うために、まず、シートをいくつか準備します。
Sheet1 の名前を「コントロール」に変更します。
このシートに後述する各試行回数(100回、1000回、10000回)のマクロを実行するためのボタンを3つ配置します。
次に、新しいシートを3枚作成します。
それぞれ「100回」「1000回」「10000回」という名前に変更します。
VBAマクロは、これらのシートに対応する試行回数の結果を書き出します。
上記のVBAコードを参考に、
RollDice_1000回 (NumRolls = 1000, 出力シート名 “1000回“)
RollDice_10000回 (NumRolls = 10000, 出力シート名 “10000回“)
のマクロも作成し、
それぞれのボタンに登録しておきましょう。
検証1:100回サイコロを振る!「偏り」を目撃せよ! (“100回” シート)
まず、「コントロール」シートの「100回振る」ボタンをクリックしてマクロを実行します。
完了メッセージが表示されたら、次に「100回」シートを開いてみましょう。
A列の A5 セル以下に、100個のサイコロの目が記録されているはずです。
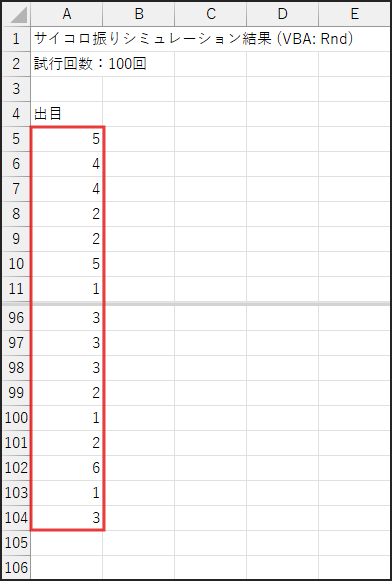
続いて、これらのデータから、1から6の各目がそれぞれ何回出現したかを集計します。
ここでは、COUNTIF 関数を使うのが一般的ですが、
今回はあえて SUM 関数と N 関数、そして比較演算子を組み合わせた、
少し「マニアック」な方法でカウントしてみましょう。
この「暇つぶし技」もExcelの奥深さを感じる一端です。
「100回」シートの例えば B 列に集計用のテーブルを作成します。
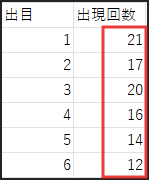
B4 セルに「出目」、C4 セルに「出現回数」と見出しを付け、B5 から B10 セルに1から6の数値を入力します。
そして、C5 セル(1の目の出現回数を表示するセル)に以下の数式を入力します。
=SUM(N($A$5:$A$104=B5))古いバージョンのExcelや特定の状況では、
入力後にCtrl + Shift + Enterキーを同時に押して確定する必要があります!
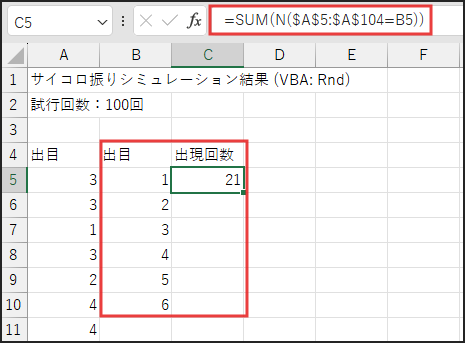
解説
A5:A104 は、VBAが出力したサイコロの出目データが記録されている範囲です。
A5:A104=B5 は、A5:A104 の各セルが B5 セル(この場合は「1」)と等しいかどうかを判定し、TRUEまたは FALSE の配列を返します。
N() 関数は、TRUE を 1 に、FALSE を 0 に変換します。
最後に SUM 関数がこれらの 1 と 0 を合計することで、
B5 セルの値(つまり「1」)が出現した回数がカウントできるのです。
この数式を C10 セルまで下にコピーすれば、各目の出現回数が集計できます。
さあ、結果はどうでしょうか?
期待通り、各目がほぼ同じ回数(100回 ÷ 6 ≒ 16.7回)ずつ出ているでしょうか?
多くの場合、特に試行回数が少ないと、結果にはバラつきが見られるはずです。
「偏り」を目で確認!ヒストグラムで可視化!
この集計結果(B4:C10 の範囲)を選択し、「挿入」タブの「グラフ」グループから「縦棒グラフ」を選んでヒストグラムを作成してみましょう。
グラフを見てください。
たった100回の試行でも、思った以上に各目の出現回数に差があり、
グラフがデコボコしていませんか?
これが、少ない試行回数で見られる「偏り」の最初の目撃です。
検証2:1,000回サイコロを振る!少しだけ均等に? (“1000回” シート)
次に、「コントロール」シートの「1000回振る」ボタンでマクロを実行し、
「1000回」シートで結果を確認します。
先ほどと同様に SUM(N()) を使って各目の出現回数を集計し、ヒストグラムを作成します。
データ範囲は A5:A1004 など、実際のデータ範囲に合わせてください
100回の時と比べてどうでしょうか?
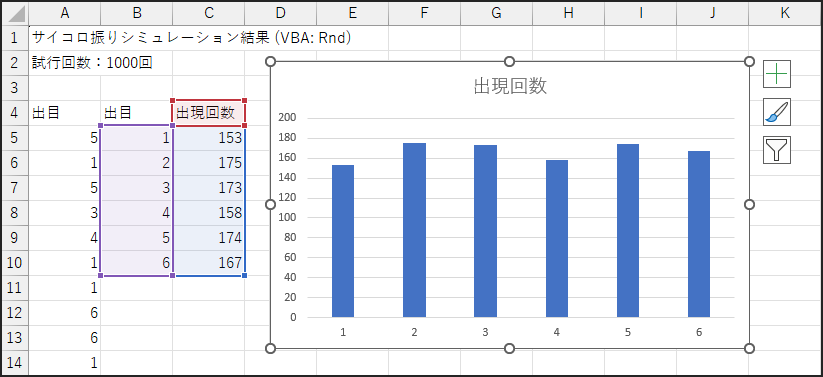
おそらく、グラフのデコボコ具合が少しだけ滑らかになり、各棒の高さの差が縮まっているかもしれません。
しかし、それでもまだ「完全に均等」とは言えず、偏りが残っているのが観察できるでしょう。
「100回よりはマシになったけど、まだ偏りが大きいですね…」と感じるかもしれません。
検証3:10,000回サイコロを振る!「大数の法則」の片鱗が見える! (“10000回” シート)
いよいよ10,000回の試行です。
「コントロール」シートの「10000回振る」ボタンを押すと、
Excelが少しの間、一生懸命計算を始めるかもしれません。
もしかしたら、マウスカーソルが砂時計になったり、
Excelのウィンドウが「応答なし」と表示されたりするかもしれませんが、
慌てずに少し待ってみましょう。
これもまた、大量データ処理の一端を体験する良い機会です。
計算が完了したら、「10000回」シートで結果を確認し、
同様に集計とヒストグラム作成を行います。
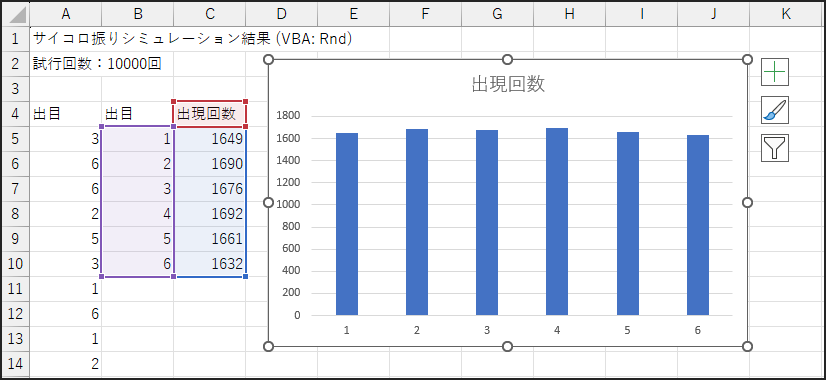
どうでしょうか?
100回や1,000回の時と比べて、10,000回のヒストグラムは、各サイコロの目の出現回数を示す棒の高さが、かなり均等に近づいてきているのが見て取れるのではないでしょうか。
完璧に同じ高さにはならないかもしれませんが、その差は以前よりもずっと小さくなっているはずです。
これが、冒頭で触れた「大数の法則」の片鱗です。
試行回数を増やすことで、実際の出現確率が理論上の確率(各目 1/6)に近づいていく様子が、視覚的に確認できたかと思います。
あなたのサイコロ、実は「偏る」!?
今回の「暇つぶし統計分析」では、ExcelとVBAを使ってサイコロ振りのシミュレーションを行い、その結果を観察しました。
一見「どうでもいいこと」に思えるこの試みから、私たちは何を見つけられたでしょうか。
「真剣にどうでもいいこと」から見えてくるExcelの奥深さ
この実験を通して、私たちはExcelの RAND 関数(正確にはVBAの Rnd 関数によるシミュレーション)が生成する乱数も、
特に試行回数が少ない場合には、私たちの期待する「完全な公平さ」からはいくらか「偏って」見えることがある、という現象を目撃しました。
実際に、100回程度の試行では、特定の目が他の目よりも多く出たり少なく出たりすることは、決して珍しくないのです。
しかし、試行回数を1,000回、10,000回と増やしていくにつれて、各目の出現割合が徐々に均等に近づいていく様子も確認できました。
これは「大数の法則」が実際に働いていることの、ほんの一端を示しています。
今回のまとめ
今回の探求から得られた主な学びは以下の通りです。
- Excelの関数やVBAを使うことで、サイコロ振りのようなランダムな事象のシミュレーションを簡単に行うことができる。
- 少ない試行回数では、乱数による結果は理論値から大きく偏ることがある。
- 試行回数を増やすことで、結果は徐々に理論値に近づいていく(大数の法則の片鱗)。
SUM(N(条件式))のような配列数式の活用も、データ集計のテクニックとして活用できる。
さて、今回の実験で「大数の法則」の片鱗は見えましたが、同時に新たな疑問も湧いてきませんか?
「では、もっともっと大量に、例えば10万回、100万回とサイコロを振り続けたら、RAND関数(またはRnd関数)は完璧な公平さを見せてくれるのだろうか?」
「そもそも、コンピュータが生み出す『乱数』とは何なのだろう?それは本当に『ランダム』なのだろうか?」
「Excelが内部で使っている『疑似乱数』のアルゴリズムとは、一体どんな秘密を持っているのだろう?」
これらの答えは、残念ながら今回の記事だけでは明らかにできません。
しかし、この探求心こそが、次なる学びへの第一歩です。
この先、さらに試行回数を増やし、Excelが持つ「疑似乱数」の性質について深く掘り下げていくと、どのような景色が見えてくるのでしょうか?
その答えは、次回の記事で!