この記事は「Excelで「大数の法則」を検証!サイコロを1万回振ると確率は収束するのか?」の続編です!
まだの方は下のリンクからどうぞ!
マクロの詳細については、Microsoft公式のヘルプも参考にしてください。
前回の続き、Excelサイコロの「真の姿」
本記事では、Excel 2021を使用して検証および数式の作成を行っています。
サイコロを振るという行為は、私たちにとって最も身近な「ランダム」な出来事の一つです。
前回の記事では、ExcelとVBAを使い、サイコロを1万回振るシミュレーションを行いました。
そして、試行回数が少ないうちは結果に「偏り」が見られるものの、
回数を増やすことで徐々に均等に近づく「大数の法則」の片鱗を目撃しました。
「どうでもいいこと」への探求、再び!
さて、1万回ではまだわずかな偏りが残っていました。
ならば、回数をさらに増やせば、いずれ完璧な公平さが得られるのでしょうか?
この「どうでもいいこと」への探求心を胸に、
今回は試行回数を10万回、そして100万回へと一気にスケールアップさせます。
Excelとあなたのパソコンの限界に挑戦し、
乱数が示す真実を一緒に追い求めていきましょう。
ExcelのRAND関数とVBAのRnd関数について
ここで、冒頭で一つ重要な点を明確にしておきます。
厳密には、VBAで乱数を生成する際にこれから使用するのは、
Excelワークシート関数のRANDではなく、VBA独自のRnd関数です。
しかし、その根底にある、コンピュータが計算によってランダムに見える数値を生成する「疑似乱数」の仕組みや、得られる数値の範囲(0以上1未満)といった点は、多くの点で共通しています。
今回は、このVBAのRnd関数が、
膨大な試行回数においてどのような振る舞いを見せるのかを追求していきます。
これは、VBAを使った壮大な「暇つぶし統計分析」の第2章です。
STEP1:超大量シミュレーションに備えよ!Excelの「隠れた設定」を制する!
これから行うのは、Excelにとって非常に負荷の高い、100万回という規模のシミュレーションです。
まずは、この膨大な計算にExcelが耐えられるよう、
VBAの「高速化」テクニックについておさらいしておきましょう。
なぜExcelは大量のデータ書き込みが苦手なのか?
VBAを使ってセルにデータを一つずつ書き込む処理。
実は、Excelにとって非常に重い作業です。
その主な原因は、データが書き込まれるたびに発生する「画面の再描画」と、
他のセルへの影響を計算する「自動計算」にあります。
100万回データを書き込むということ、それは…、
これらの処理が100万回繰り返されることを意味します。
何も対策をしなければ膨大な時間がかかってしまいます。
そこで、これらの処理を一時的に停止することで、
マクロの実行速度を劇的に向上させるのです。
VBAの「高速化」テクニックを再確認!
高速化の鍵となるのは、以下の2つの命令です。
Application.ScreenUpdating = False
これは「画面の描画を停止せよ」という命令です。
マクロの実行中は画面の変化を一切表示しなくなります。
Excelは描画処理にリソースを割く必要がなくなり、本来の計算処理に集中できます。
Application.Calculation = xlCalculationManual
これは「計算方法を手動に切り替えよ」という命令です。
通常、Excelはどこかのセルの値が変わると、関連する数式をすべて自動で再計算します。
これを、マクロ実行中だけ停止させます。
不要な計算の繰り返しを防ぎます。
特に10万回、100万回といった規模の処理では、その効果は絶大です。
STEP2:サイコロを「10万回」振る!「大数の法則」が本格的に動き出す! (“10万回” シート)
準備が整いました。
いよいよ、最初の大きな挑戦である「10万回」のシミュレーションです。
ここから、Excelが本格的にその計算能力を発揮し始めます。
VBAコードの作成と実行
まず、前回のファイルに追記する形で準備をします。
「コントロール」シートに「10万回実行」用のマクロ実行ボタンを新たに設置します。
「10万回」という名前の新しいシートを作成します。
次に、VBAエディタを開き、以下の RollDice_10万回 マクロのコードを追記します。
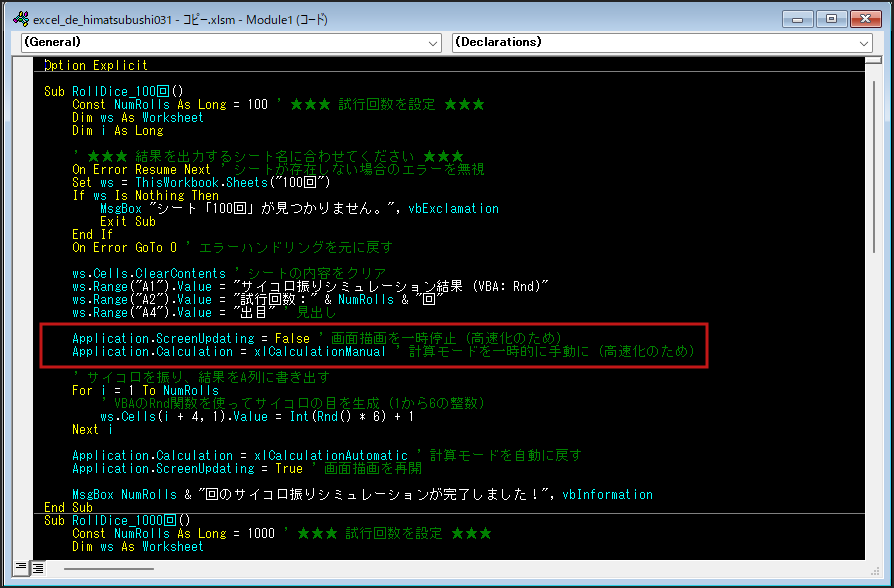
Sub RollDice_10万回()
Const NumRolls As Long = 100000 ' ★★★ 試行回数を10万回に設定 ★★★
Dim ws As Worksheet
Dim i As Long
Set ws = ThisWorkbook.Sheets("10万回") ' 結果を出力するシート名
ws.Cells.ClearContents ' シートをクリア
ws.Range("A1").Value = "サイコロ振りシミュレーション結果"
ws.Range("A2").Value = "試行回数:" & NumRolls & "回"
ws.Range("A4").Value = "出目" ' 見出し
' --- 高速化設定 ---
Application.ScreenUpdating = False
Application.Calculation = xlCalculationManual
For i = 1 To NumRolls
ws.Cells(i + 4, 1).Value = Int(Rnd() * 6) + 1
Next i
' --- 設定を元に戻す ---
Application.Calculation = xlCalculationAutomatic
Application.ScreenUpdating = True
MsgBox NumRolls & "回のサイコロ振りシミュレーションが完了しました!"
End Sub
さあ、いよいよExcelが本気を出す時が来ました!
作成したボタンをクリックしてマクロを実行し、
お使いのPCの性能によっては、かすかな「うなり声」が聞こえるかもしれません。
そのプロセスも、ぜひ体験してみてください。
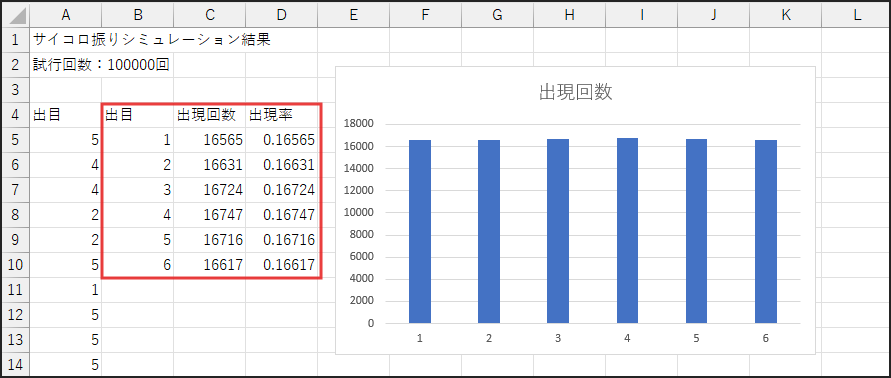
10万回サイコロを振った結果、偏りはどうなった?
計算が完了したら、「10万回」シートの結果を見ていきます。
前回と同じく、SUM(N(範囲=条件)) の数式を使って各目の出現回数を集計し、
その結果を棒グラフで可視化します。
さらに、今回は各目の出現率(パーセンテージ)も計算してみましょう。
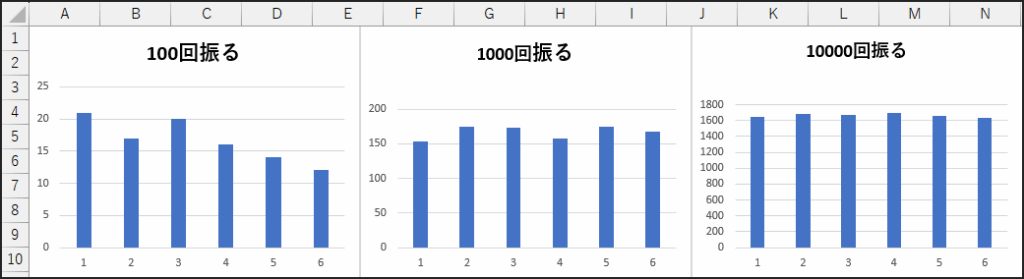
1万回のヒストグラムと比較すると、どうでしょうか?
棒の高さの差が、格段に小さくなっているのが一目瞭然のはずです。
偏りが、目に見えて薄くなってきましたね!
パーセンテージを見てみると、全ての目が理論値である16.667%に非常に近い値を示していることが、数値からも確認できるでしょう。
STEP3:究極の挑戦!サイコロを「100万回」振る!乱数の真の姿を拝め! (“100万回” シート)
10万回でも驚くほど均等に近づきましたが、私たちの探求はここで終わりません。
次なる舞台は、まさに究極の挑戦、「100万回」です。
VBAコードの作成と実行
準備はこれまでと同様です。
「コントロール」シートに「100万回実行」ボタンを設置し、
「100万回」という名前のシートを新たに作成します。
そして、以下の RollDice_100万回 マクロをVBAエディタに追加してください。
Sub RollDice_100万回()
Const NumRolls As Long = 1000000 ' ★★★ 試行回数を100万回に設定 ★★★
Dim ws As Worksheet
Dim i As Long
Set ws = ThisWorkbook.Sheets("100万回") ' 結果を出力するシート名
ws.Cells.ClearContents ' シートをクリア
ws.Range("A1").Value = "サイコロ振りシミュレーション結果"
ws.Range("A2").Value = "試行回数:" & NumRolls & "回"
ws.Range("A4").Value = "出目" ' 見出し
' --- 高速化設定 ---
Application.ScreenUpdating = False
Application.Calculation = xlCalculationManual
For i = 1 To NumRolls
ws.Cells(i + 4, 1).Value = Int(Rnd() * 6) + 1
Next i
' --- 設定を元に戻す ---
Application.Calculation = xlCalculationAutomatic
Application.ScreenUpdating = True
MsgBox NumRolls & "回のサイコロ振りシミュレーションが完了しました!"
End Sub
これはまさに、Excelにとって真剣勝負です。
実行ボタンを押してから、完了のメッセージボックスが表示されるまで、
しばしの待ち時間が発生します。
PCのファンが力強く回転を始めるのを感じながら、Excelが膨大なデータを処理する様子を想像してみてください。
この待ち時間の先に、乱数の真の姿が広がっています。
100万回サイコロを振った結果、乱数は完璧な「公平」を手に入れたのか?
長い計算の末に得られた100万個のデータ。
早速、集計してグラフで可視化してみましょう。
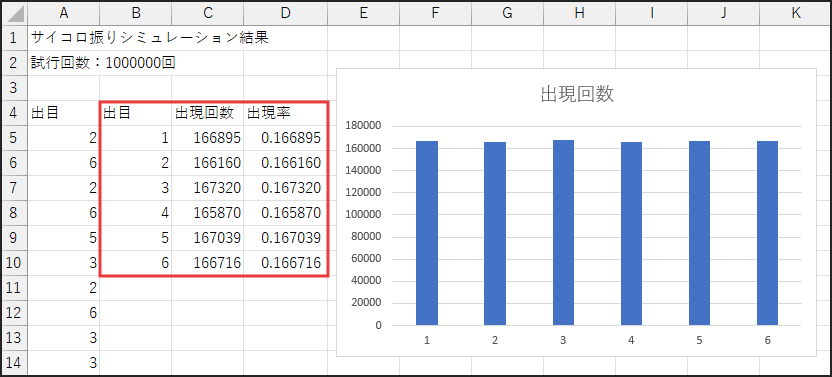
ヒストグラムの6本の棒は、まるで精密に設計されたかのように、ほぼ完璧に同じ高さで並んでいます。
これが、「大数の法則」が示す圧倒的な証明です。
パーセンテージ表示を見れば、各目の出現率と理論値16.667%との差が、
もはや誤差としか言えないほど限りなく小さくなっていることがわかります。
これが、VBAの Rnd 関数と「大数の法則」が描き出す、乱数の「真の姿」なのです。
STEP4:「真のランダム」と「疑似乱数」の違い
100万回の試行を経て、私たちは乱数が示す驚くべき均等な結果を目の当たりにしました。
では、この結果をもって「Excelのサイコロは完全に公平だ」と言えるのでしょうか?
その答えを探るため、もう少しだけ乱数の世界の深淵を覗いてみましょう。
実験結果が示すRnd関数の特性
今回の実験を通じて、VBAの Rnd 関数(Excelの RAND 関数も同様)が生成する乱数は、
試行回数を重ねることで限りなく均等に近づく、非常に優れた統計的性質を持つことがわかりました。
しかし、これらは「真のランダム」ではありません。
コンピュータは、ある計算式(アルゴリズム)に基づいて、
ランダムに見える数値の列を生成しています。
これが「疑似乱数」と呼ばれるものです。
つまり、その性質はあくまで「ランダムに限りなく近い」のであり、
予測不可能な物理現象などから生まれる「真のランダム」とは区別されます。
ですが、心配は無用です。
この疑似乱数の品質は非常に高く、今回のようなシミュレーションや多くの科学技術計算において、
実用上は「真のランダム」と見分けがつかないほど信頼できるものです。
自然なランダムに見せるためのひと手間
VBAには Randomize という命令文があります。
これは、疑似乱数を生成する際の出発点(シード値)を、
PCのシステム時刻などを使って初期化する役割を持ちます。
マクロの最初に Randomize と一行書き加えるだけで、
Excelを起動するたびに異なるパターンの乱数列が生成されるようになり、
見かけ上のランダム性がさらに高まります。
いわば、よりランダムに見せるための「おまじない」のようなものです。
今回の実験では割愛しましたが、より厳密なシミュレーションを行う際には覚えておくと良いでしょう。
まとめ:Excelは「確率の実験」 乱数の謎を解き明かせ!
10万回、そして100万回という壮大なシミュレーションを通じて、
私たちは「大数の法則」の圧倒的な力を体験しました。
この探求は、ExcelとVBAが持つ奥深い可能性を改めて教えてくれます。
今回の壮大な暇つぶしから、私たちは多くのことを学びました。
Excelの計算能力と、VBAによる自動化・高速化技術を組み合わせることで、
複雑な確率シミュレーションがデスクトップ上で可能になることの面白さを実感できたのではないでしょうか。
もう、あなたのPCはただの表計算ソフトではありません。
大量のサイコロを振る「製造所」であり、
確率を検証する「実験室」なのです。
今回のシミュレーションは、Excelのセル一つずつにデータを書き込むという、比較的シンプルな方法を採りました。
しかし、VBAにはもっと高速に、一瞬で大量のデータをシートに書き込むテクニックが存在します。
次の記事では、そのVBAの「配列一括書き込み術」を徹底解説し、
今回の100万回シミュレーションをさらに高速化する方法を探求します。