Excel縛りプレイ！関数のみで「-1」を生成せよ

本記事では、Excel 2021を使用して検証および画像の作成を行っています。

Excelの関数のみで「-1」を作り出せ！数値・演算子、一切使用禁止の関数パズル！

「Excelで『-1』って…セルに–と1を入力するだけじゃないの？」

そう思ったあなた、もちろん大正解！

普通は、それで100点満点です。

でも、ちょっと待ってください！
ここは「Excelで暇つぶし」をするブログです。

そんな当たり前の方法では、知的好奇心は満たされませんよね？

今回は、Excelに、厳しい「縛り」を与えた上で、この一見単純な「-1」という数値の生成に挑戦します。

「え、縛りって…？まさか、-（マイナス）の記号が使えないとか…？」

そのまさかです！
しかも、それだけではありません！今回のルールは、過去最高レベルに厳しいですよ！

さあ、あなたのExcel力の限界に、一緒に挑んでみましょう！

今回のミッション

ゴール

目指すゴール: Excelのワークシート関数のみを使い、単一のセルに「-1」という数値を表示させる。

ルール：厳格な関数縛り！

使用できるのはワークシート関数のみ。
数式内に数値・文字列・演算子などの記号の直接記述は一切禁止。
（例: 5, "A", "+", "&" などの直接入力は全てNG！）
同一関数の複数回使用の禁止。
（例: =SUM(N(TRUE),N(TRUE)) のような使用は不可）
1つの関数に指定できる引数は最大2つまで。
（例: =SEQUENCE(1,2,3) のような3引数の使用は不可）
ROW関数COLUMN関数禁止
関数の入れ子（ネスト）構造の使用は自由。
どのExcelバージョンの関数でも使用可能。

つまり、数式に使用していい文字は= ( ) , とアルファベットのみということです！

方法1：三角関数を利用する

考えかた

まず思いつくのは、数学の世界で「-1」になる有名な公式を利用する方法です。

高校数学を思い出してください…そう、三角関数です！

コサイン（cos）やサイン（sin）を使えば、特定の角度で「-1」を導き出せそうですね。

数式と解説

数式 ① =COS(PI())

これは、今回のパズルにおける最もシンプルで、美しい解答の一つです。

PI() = 3.141592…
PI(): 引数なしで、円周率π（パイ）の値を返します。
COS(3.141592...) = -1
COS(数値): 指定された角度（ラジアン）のコサインを返します。

数学的にcos(π) = -1です。

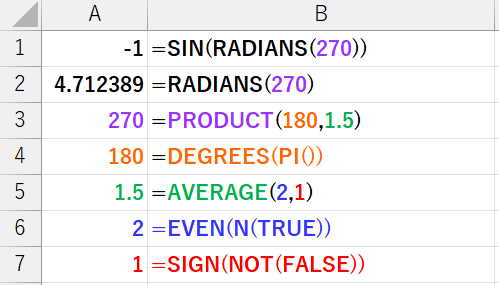
数式 ② =SIN(RADIANS(PRODUCT(DEGREES(PI()),AVERAGE(EVEN(N(TRUE)),SIGN(NOT(FALSE))))))

「COSが使えるなら、SINでもいけるはず！」という探求心が生み出した、超絶技巧の数式です！

SIN関数で-1を出すにはSIN(270°)を計算する必要がありますが、ルールで数値の270は使えません。

そこで、関数を何重にも組み合わせ、この270という数値を無理やり作り出したのが、この数式です。

計算過程と関数の役割

N(TRUE) = 1
N(値): 値を数値に変換します。TRUEは1に、FALSEは0になります。
NOT(FALSE) = TRUE
NOT(論理値): 論理値を逆にします。TRUEはFALSEに、FALSEはTRUEになります。
SIGN(TRUE) = 1
SIGN(数値): 数値の符号を返します。正なら1、負なら–1、ゼロなら0です。TRUEは1として扱われます。
EVEN(1) = 2
EVEN(数値): 数値を最も近い偶数に切り上げた値を返します。
AVERAGE(2, 1) = 1.5
AVERAGE(数値1, [数値2]): 引数の平均値（相加平均）を返します。
DEGREES(PI()) = 180
DEGREES(角度): ラジアンで表された角度を、度に変換します。PI()は180°です。
PRODUCT(180, 1.5) = 270
PRODUCT(数値1, [数値2]): 引数をすべて掛け合わせた結果（積）を返します。
RADIANS(270) = 4.712388… (3π/2ラジアン)
RADIANS(角度): 度で表された角度を、ラジアンに変換します。
SIN(4.712388...) = -1
SIN(数値): 指定された角度（ラジアン）のサインを返します。

方法2：対数を利用する

考えかた

三角関数の次は、対数（ログ）の世界を探検してみましょう。

対数関数には、「1より小さい正の数の対数は、必ず負の数になる」という面白い性質があります。

これを利用すれば、「-1」への道筋が見えてきそうです。

数式と解説

数式 ③ =SIGN(LN(RAND()))

この数式も、非常に数学的です。

計算過程と関数の役割

RAND() = 0.12345 (0から1の間の乱数を生成)
RAND(): 引数なしで、0以上1未満の乱数を返します。

LN(0.12345) = -2.0919… (結果は必ず負の数)
LN(数値): 数値の自然対数（底がeの対数）を返します。

SIGN(-2.0919...) = -1 (負の数の符号は-1)

数式 ④ Excelの画像=LOG(EVEN(N(TRUE)),IMDIV(PRODUCT(ISNA(NA())),ROUNDUP(SQRT(PI()),SUM(FALSE))))

数学的に、log₂(0.5)は-1になります。

この数式は、あの手この手で関数を組み合わせ、底が2、真数が0.5になるように計算しているのです。

計算過程と関数の役割

EVEN(N(TRUE)) = 2
（これがLOGの底になります）
NA() = #N/A
NA(): 引数なしで、#N/A（値が見つからない）というエラー値を返します。
ISNA(#N/A) = TRUE
ISNA(値): 値が #N/A エラーであるかどうかを判定し、TRUEまたはFALSEを返します。
PRODUCT(TRUE) = 1
SUM(FALSE) = 0
SUM(数値1, [数値2]): 引数をすべて合計した結果（和）を返します。FALSEは0として扱われます。
SQRT(PI()) = 1.772…
SQRT(数値): 正の平方根を返します。
ROUNDUP(1.772..., 0) = 2
ROUNDUP(数値, 桁数): 数値を指定された桁数に切り上げます。
IMDIV(1, 2) = 0.5
（これがLOGの真数になります）
IMDIV(複素数1, 複素数2): 複素数同士の割り算（商）を計算します。実数にも使えます。
LOG(2, 0.5) = -1
LOG(数値, [底]): 指定された底に対する数値の対数を返します。

方法3：文字列の力技で「-1」を組み立てる

考えかた

ここからは、数学的なアプローチとは全く違う、Excelならではの「力技」の世界です。

発想を転換してみましょう。

「-1」という数値が作れないなら、「-」という文字と「1」という文字を別々に作って、最後に合体させればいいじゃないか！という作戦です。

数式と解説

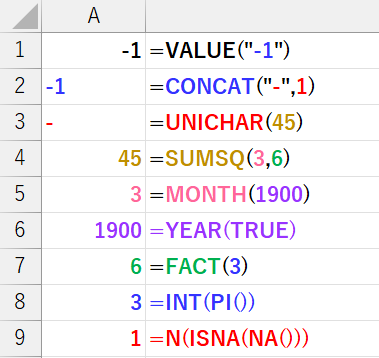
数式 ⑤ =VALUE(CONCAT(UNICHAR(SUMSQ(MONTH(YEAR(TRUE)),FACT(INT(PI())))),N(ISNA(NA()))))

この数式の心臓部は、UNICHAR(45)です。これは、文字コード45に対応する「–」（マイナス記号）を返します！

計算過程と関数の役割

YEAR(TRUE) = 1900
YEAR(シリアル値): 日付を表すシリアル値から「年」の部分を整数で返します。TRUEはシリアル値1（1900年1月1日）として扱われます。
MONTH(1900) = 3
MONTH(シリアル値): 日付のシリアル値から「月」を返します。1900は1905年3月14日として解釈されるため3が返ります。
INT(PI()) = 3
INT(数値): 数値の小数点以下を切り捨てて整数にします。
FACT(3) = 6
FACT(数値): 数値の階乗を返します (3×2×1=6)。
SUMSQ(3, 6) = 45
SUMSQ(数値1, [数値2]): 引数の2乗の合計を返します (3²+6²=9+36=45)。
UNICHAR(45) = “–“
UNICHAR(数値): 指定された数値に対応するUnicode文字を返します。
N(ISNA(NA())) = 1
CONCAT("-", 1) = “-1”
CONCAT(文字列1, [文字列2]): 複数の文字列を一つの文字列に結合します。
VALUE("-1") = -1
VALUE(文字列): 数値を表す文字列を、実際の数値に変換します。

方法4：「減算」の概念をハックする

考えかた

演算子「–」が使えないなら、減算ができない…。

本当にそうでしょうか？

Excelには、一見すると全く関係ないのに、内部的に「引き算」を行ってくれる関数が、いくつか存在するのです！

数式と解説

数式 ⑥ =DAYS(N(TRUE),EVEN(RAND()))

「え、DAYS関数！？日付の計算でなぜマイナスが…？」

そう思いますよね！

計算過程と関数の役割

N(TRUE) = 1 (終了日: 1900/1/1)
EVEN(RAND()) = 2 (開始日: 1900/1/2)
DAYS(1, 2) = -1
DAYS(終了日, 開始日): 2つの日付の間の日数を返します。内部的には「1 – 2」が実行されます。

数式 ⑦ =VALUE(IMSUB(N(TRUE),EVEN(RAND())))

IMSUB関数は複素数の引き算を行う関数ですが、実数を引数にすると、単純な引き算の結果を「文字列」で返します。

計算過程と関数の役割

N(TRUE) = 1
EVEN(RAND()) = 2
IMSUB(1, 2) = “-1”
IMSUB(複素数1, 複素数2): 複素数同士の引き算（差）を計算します。実数にも使えます。
VALUE("-1") = -1

数式 ⑧ =SUMX2MY2(N(FALSE),SIGN(TRUE))　※数式に数字あり

このSUMX2MY2関数は、2つの配列の「二乗の差の合計」を求める関数です。

計算過程と関数の役割

N(FALSE) = 0
SIGN(TRUE) = 1
SUMX2MY2(0, 1) = -1
SUMX2MY2(配列1, 配列2): 2つの配列の「二乗の差の合計」（Σ(x²-y²)）を返します。内部で0² – 1²が計算されます。

ただ、この関数名に含まれる「2」が、ルールの「数値の直接記述禁止」に抵触するのでは…？という、哲学的な論争を呼ぶかもしれませんね！

方法5：複素数の定義を利用した正攻法

考えかた

いよいよ最後のアプローチです。

数学の世界に、「2乗すると-1になる数」が存在するのを覚えていますか？

そう、虚数単位「i」です！

このi² = -1という、複素数の根本的な定義を利用すれば、非常にエレガントに「-1」を導き出せそうです。

数式と解説

数式 ⑨ =IMREAL(IMPOWER(COMPLEX(SUM(FALSE),N(TRUE)),EVEN(RAND())))

この数式は、まさにi² = -1をExcel関数で表現したものです。

計算過程と関数の役割

COMPLEX(SUM(FALSE),N(TRUE)) = “i” (実部0, 虚部1の複素数)
COMPLEX(実数, 虚数): 実数と虚数を基に、x+yiまたはx+yj形式の複素数（文字列）を生成します。
EVEN(RAND()) = 2
IMPOWER("i", 2) = “-1”
IMPOWER(複素数, 指数): 複素数を指定した指数でべき乗した結果を返します。
IMREAL("-1") = -1
IMREAL(複素数): 複素数の実数部分（係数）を返します。