本記事では、Excel 2021を使用して検証および画像の作成を行っています。
SUMとSEQUENCEの挑戦状！「a+b+c+d」の最小値を探せ！
「ふーん、SUMとSEQUENCEね。どっちもよく使う便利な関数じゃないか。」
そう思ったあなた、その通り！
SUMは合計、SEQUENCEは連続した数値の配列を作成する、どちらも非常に便利で、実務でも頻繁に登場する優秀な関数です。
では、この二つを組み合わせた、以下のシンプルな数式はいかがでしょう？
=SUM(SEQUENCE(a,b,c,d))
この数式の結果が、ちょうど「10000」になるとき、4つの変数a,b,c,dの合計値、つまりa+b+c+dが最も小さくなる組み合わせは、一体何になるでしょうか？
一見、単純な力技で解けそうに見えるこの問題…。
しかし、その裏には美しい数学的アプローチが隠されています。
今回は、Excelでの試行錯誤を通じて、論理的に最適解を導き出す、そんな思考のプロセスを一緒に楽しむ「暇つぶし」です！
今回のミッション
ゴール
=SUM(SEQUENCE(a,b,c,d))の結果が10000になるとき、a+b+c+dの合計値の最小値を求める。
ルール：変数は「自然数」のみ！
今回の挑戦では、a,b,c,dに使用できるのは自然数（1以上の整数）のみとします。
なぜなら、もしc（SEQUENCEの開始値）に負の数を使うことを許可してしまうと、a+b+c+dの合計値をいくらでも小さくできてしまい、パズルが成立しなくなってしまうからです。
例えば、=SUM(SEQUENCE(10,10,-10097,206))という数式は、結果が10000になりますが、このときのa+b+c+dは10+10-10097+206 = -9871となり、cの値を調整すれば、マイナス無限大まで作り出せてしまいます。
この制約こそが、今回のパズルを奥深く、面白くするスパイスなのです。
主役となる関数たち
SEQUENCE関数
SEQUENCE(行, [列], [開始], [間隔])
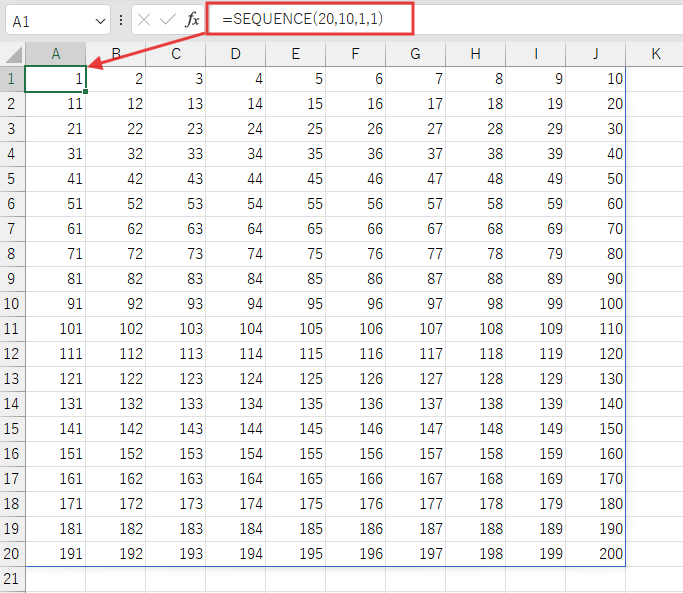
SEQUENCE関数は、連続した数値の配列（メモリ上に広がる仮想的な表）を生成する、非常に強力な関数です。
- 行: 作成する配列の行数を指定します。
- [列]: 作成する配列の列数を指定します。（省略すると
1） - [開始]: 配列の最初の数値を指定します。（省略すると
1） - [間隔]: 次の数値までの増分（ステップ）を指定します。（省略すると
1）
SUM関数
SUM(数値1, [数値2], ...)
SUM関数は、指定された数値やセル範囲の合計値を計算する、おなじみの関数ですね。
今回は、SEQUENCE関数が生成した配列を、このSUM関数で合計する、というわけです。
[Excelバージョンの補足]SUM(SEQUENCE(...))という数式は、Excel 2021やMicrosoft 365のような、スピルに対応したバージョンであれば、Enterキーだけで計算できます。
しかし、Excel 2019以前のバージョンでは、これは「配列数式」として扱われるため、数式を入力した後に Ctrl + Shift + Enter を同時に押して、数式を{}で囲む必要があります。
ちなみに、このような配列の合計を計算する場合、古いExcelではSUM関数の代わりにSUMPRODUCT関数を使うことで、CSE確定を不要にする、というテクニックも広く使われています。
STEP1：まずは試行錯誤！手当たり次第に探ってみる
考えかた
さて、ルールと関数の役割が分かったところで、早速パズルを解きにかかりましょう！
まずはExcelの得意技、とにかく数字を当てはめてみる「試行錯誤」アプローチです。
「aとbを小さくしたらどうなる？」「じゃあcとdを最小にしてみたら？」と、色々試してみましょう。
検証①：aとbを最小にしてみる
a+b+c+dを小さくしたいのですから、まずはaとbに最小の自然数である1を入れてみましょう。
a=1, b=1
この場合、SEQUENCE関数が作る配列の要素は、たったの一つだけです。
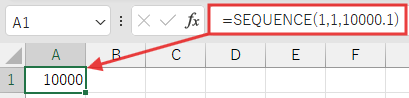
=SUM(SEQUENCE(1,1,c,d))は、当然ながらcそのものを返します。
つまり、c=10000となります。dは最小の1とすると…
a=1, b=1, c=10000, d=1a+b+c+d = 1+1+10000+1 = 10003
うーん、合計値が10003。
なんだか、もっと小さくできそうな気がしますね…。
検証②：cとdを最小にしてみる
では逆に、cとdに最小の自然数である1を入れてみましょう。
c=1, d=1
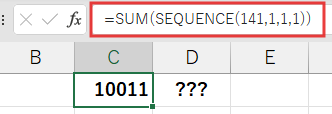
この場合、数式は=SUM(SEQUENCE(a,b,1,1))となります。
これは、「1から始まる連続した整数を、a×b個ぶん合計する」という意味になりますね。
例えばa=4, b=5なら、1から20までを合計する、ということです。
この数式の結果が10000になるaとbを探すわけですが…。
小まとめ：「力任せ」では、夜が明けてしまう…！
「あぁでもない、こうでもない…」
色々と試してみたものの、なかなか答えにたどり着きません。c=1, d=1のケースを数学的に解こうとしても、n(n+1)/2 = 10000となる整数n（=ab）は存在しません。
力任せの試行錯誤だけでは、答えにたどり着くのは非常に難しそうです。
どうやら、もっとスマートなアプローチが必要なようですね…。
STEP2：Excelの数式を「数学の言葉」に翻訳する
考えかた
行き詰まった時こそ、一歩引いて、問題の本質を見つめ直すチャンスです。
このExcelの数式が、数学的に何を意味しているのかを考えてみましょう。「急がば回れ」の精神です！
等差数列の和
SEQUENCE(a,b,c,d)が作る数列は、
- 初項 =
c - 項数 =
a b - 公差 =
d
の等差数列です。
そして、その末項（最後の項）は、c + ((a b) - 1) d と表せます。
等差数列の和の公式は、(項数 / 2) × (初項 + 末項) でしたね。
数式モデルの構築
この公式に、先ほどの要素を当てはめてみましょう。
10000 = ( (ab) / 2 ) ( c + (c + (ab-1)d) )
これを整理すると…
10000 = (ab / 2) (2c + (ab-1)d)
さらに両辺を2倍すると、
20000 = (ab) (2c + (ab-1)d)
どうでしょう！
Excelの数式が、a,b,c,dの関係性を明確に示す、美しい一本の数式モデルに変換できました。
これこそが、この難解なパズルを解き明かす、最強の武器です。
STEP3：数学の力で「探索範囲」を絞り込む
考えかた
この数式モデルを手に入れた私たちは、もう闇雲に数字を探す必要はありません。
論理の力で、探索範囲を一気に絞り込んでいきましょう。
ヒント1：「ab」は20000の約数である
この数式の形から、abは20000の約数でなければならない、ということが分かります。
これは非常に大きなヒントですね！
ヒント2：「ab」の上限を見つける
次に、abがどれくらいの大きさになりうるのか、その上限を探ります。
cとdは自然数なので、最小値は1です。
仮にc=1, d=1を数式モデルに代入してみましょう。
20000 = (ab) (21 + (ab-1)1)
20000 = (ab) (ab + 1)
abをNと置くと、20000 = N (N+1)となります。
√20000は、だいたい141.4です。
141 142 = 20022なので、N（つまりab）は、*141より小さい**ことが確定しました。
これで、無数にあった可能性の中から、「141未満の、20000の約数」という、極めて限られた候補だけを調べればよくなったのです！
STEP4：最強の組み合わせを見つけ出す！
考えかた
さあ、論理の網で候補を絞り込みました。いよいよ、最小値となる組み合わせを突き止める時です！
a+b+c+dを最小にするには、各変数のバランスが重要です。
abが小さすぎるとcが巨大になり、abが大きすぎるとa+bが大きくなる可能性があります。
STEP3で絞り込んだ候補の中から、141に近く、キリの良いab = 100を試してみましょう。
最終検証：ab = 100のケース
ab = 100を、私たちの武器である数式モデルに代入します。
20000 = 100 (2c + (100-1)d)
200 = 2c + 99d
この式を満たす、自然数cとdを探します。
d=1の場合:200 = 2c + 99→101 = 2c。残念ながらcが整数になりません。d=2の場合:200 = 2c + 198→2 = 2c→c=1！ 見つかりました！
これで、c=1, d=2が確定しました。
次に、ab=100で、a+bが最小になる組み合わせを探します。
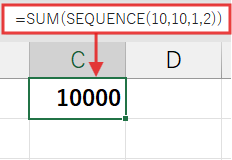
これは、aとbが最も近い数値の時、つまりa=10, b=10ですね。
結論
全てのピースが揃いました。
最小値を実現する組み合わせは…
- a = 10
- b = 10
- c = 1
- d = 2
であり、その合計値a+b+c+dは、10 + 10 + 1 + 2 = 23 となります！
実務で役に立つ？この思考法の意外な使い道
「なるほど、パズルは解けたけど、これって結局、実務では何の役にも立たない知識じゃないか！」
そう思われたかもしれませんね。確かに、この数式そのものを実務で使うことはないでしょう。
しかし、このパズルを解くために辿った「思考のプロセス」こそが、実は様々な分野で応用できる、非常に強力な武器になるのです。
今回のプロセスを振り返ってみましょう。
- 問題を定義する (
SUM(SEQUENCE)=10000の最小値) - Excelの機能を、数学的なモデルに落とし込む (数式化)
- モデルを分析し、制約条件を見つける (
Nは20000の約数、かつ141未満) - 絞り込んだ範囲で、最適解を探し出す
この思考プロセスは、例えばデータ分析や経営企画といった分野で日常的に行われています。
「売上目標=10000を達成するために、広告費(a), 営業日数(b), 単価(c), インセンティブ(d)の合計コストを最小化したい」
といったビジネス上の最適化問題は、まさに今回のパズルと同じ構造をしています。
この「暇つぶし」を通じて、知らず知らずのうちに、複雑な問題を解決するための、本質的な思考のトレーニングをしていたのです。
まとめ
今回は、SUMとSEQUENCEというシンプルな関数から始まる、奥深い関数パズルに挑戦しました。
手当たりの試行錯誤から始まり、数学的なアプローチを経て、美しい最適解にたどり着いた旅はいかがでしたでしょうか。
シンプルなExcelの数式も、少し視点を変えるだけで、これほどまでに奥深い思考のトレーニングになるのです。
このパズルが、あなたの「Excelで暇つぶし」の時間を、さらに豊かで刺激的なものにする一助となれば、これほど嬉しいことはありません。
- Excel関数パズル！SUMとSEQUENCEで最小値を探せ
- Excel縛りプレイ！関数のみで「i」を生成せよ
- Excel縛りプレイ！関数のみで「-1」を生成せよ
- INDEXとINDIRECTの三重奏！Excelで動的参照を操る
- 作曲が変わる音楽理論！和音の「機能」で全てを解く
