本記事では、OSを問わず誰でも無料で利用できる「Web版Excel」を使用して検証および画像の作成を行っています。MacやLinuxユーザーの方も、ブラウザさえあれば一緒に挑戦できますよ！
PI関数は禁止！Excelで「円周率π」の近似値を求める、壮大な暇つぶし！
「Excelで円周率？…そんなの=PI()って入力すれば、一瞬で『3.14159265…』って出るじゃないか。」
そう思ったあなた、もちろん大正解！
Excelに用意されているPI関数を使うのが、最も簡単で、最も正確な方法です。実務では100点満点の回答ですね。
でも、ここは「Excelで暇つぶし」をするブログ。
答えが分かっている道を、ただ最短距離で歩くだけでは、面白くないですよね？
今回は、あえてその便利なPI関数を禁止するという縛りを設けて、人類が何世紀にもわたって挑んできた「円周率の探求」の歴史を、Excelの関数を使って追体験してみよう、という壮大な挑戦です。
「え、そんなことできるの？しかもWeb版のExcelで？」
できるんです！
今回は、歴史的な数学の公式「ライプニッツ級数」と、確率統計の考え方を使った「モンテカルロ法」という、全く異なる2つのアプローチで、円周率の近似値に迫ります！
この探求を通して、あなたのExcelスキルだけでなく、数学の世界への興味も深まること間違いなし！
さあ、Excelで数学の歴史を巡る、知的な「暇つぶし」の旅に出かけましょう！
方法1：ライプニッツ級数 – 無限の足し算と引き算でπに迫る！
考えかた
最初にご紹介するのは、17世紀のドイツの数学者・哲学者であるゴットフリート・ライプニッツが発見した、非常に美しい公式です。
その名も「ライプニッツ級数」
数式で書くと、こうなります。
π/4 = 1 – 1/3 + 1/5 – 1/7 + 1/9 – …
なんと、分母が奇数の分数を、プラスとマイナスを交互に無限に繰り返していくと、その合計が「π/4」になるというのです！
ということは、この計算結果を4倍すれば、円周率πの近似値が求められる、というわけですね。
「でも、無限に計算なんてできないじゃないか。どうやってExcelでやるの？」
良い質問です！もちろん、無限回の計算は不可能ですが、この計算を「非常にたくさん」繰り返せば、かなり近い値になるはずです。
今回は、ExcelのSEQUENCE関数を使って、この気の遠くなるような計算を、たった一つの数式で実現してみせます！
数式と解説
=PRODUCT(SUM(1/SEQUENCE(1000000,1,1,4))-SUM(1/SEQUENCE(1000000,1,3,4)),4)
この数式は、2つの巨大なSEQUENCE関数を使い、ライプニッツ級数の「プラスの項」と「マイナスの項」を別々に計算し、最後にそれらを合体させる、という非常に巧妙なロジックで成り立っています。
数式の分解解説
- プラスの項の計算: SUM(1/SEQUENCE(1000000,1,1,4))
SEQUENCE(1000000,1,1,4): まず、SEQUENCE関数で「開始値1、間隔4」の数列を100万個作ります。これにより、1, 5, 9, 13, …という、プラスの項の分母だけが生成されます。1/...: 生成された各数値を逆数にします。（1, 1/5, 1/9, …）SUM(...): 最後に、これらの逆数をすべて合計します。
- マイナスの項の計算: SUM(1/SEQUENCE(1000000,1,3,4))
SEQUENCE(1000000,1,3,4): 今度は「開始値3、間隔4」で数列を作り、3, 7, 11, 15, …という、マイナスの項の分母だけを生成します。- 同様に、これらの逆数をSUM関数で合計します。
- 合体と仕上げ
(プラスの項の合計) - (マイナスの項の合計): これでπ/4の近似値が求まります。PRODUCT(..., 4): 最後にPRODUCT関数で結果を4倍し、円周率πの近似値を算出します！
100万項まで計算しても、なかなか「3.14159265358…」には近づきませんが、人類がかつて手計算で挑んだ歴史の重みを、感じられるのではないでしょうか。
方法2：モンテカルロ法 – 無数の点を打ち、確率でπを求める！
考えかた
次にご紹介するのは、先ほどの数式とは全く違う、確率と統計の考え方を使った「モンテカルロ法」です。
これは、カジノで有名なモナコ公国のモンテカルロ地区から名付けられた手法で、一見するとランダム（でたらめ）な試行を大量に繰り返すことで、近似解を求めるという面白いアプローチです。
円周率を求めるための考え方は、非常にシンプルです。
まず、一辺が2の正方形（面積4）を描き、その中にぴったり収まる半径1の円（面積π）を描きます。
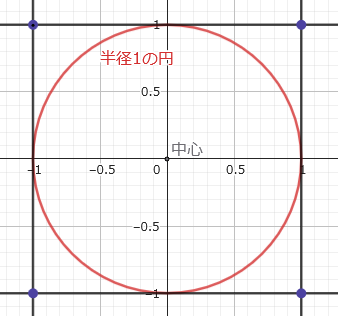
次に、この正方形の中に、完全にランダムな点を、目をつぶって大量に打ち込みます。
全ての点を打ち終わった後、円の内側に入った点の数と、全体の点の数の比率を調べます。
この「点の比率」は、ほぼ「円の面積と正方形の面積の比率」に等しくなるはずです。
つまり、(円の中の点 / 全ての点) ≒ (円の面積 / 正方形の面積) = (π / 4)となります。
ということは、この「点の比率」を4倍すれば、円周率πの近似値が求められる、というわけです！
数式と解説
この一見、アナログな手法を、Web版ExcelのRANDARRAY関数と、複素数関数を駆使して、デジタルに再現してみましょう！
STEP1: RANDARRAYでランダムな点を10万個生成
まず、A1セルに以下の数式を入力します。
=RANDARRAY(100000,2,-1,1,FALSE)
RANDARRAY(行数, 列数, 最小値, 最大値, 整数にするか): 指定したサイズのランダムな数値の配列を生成します。
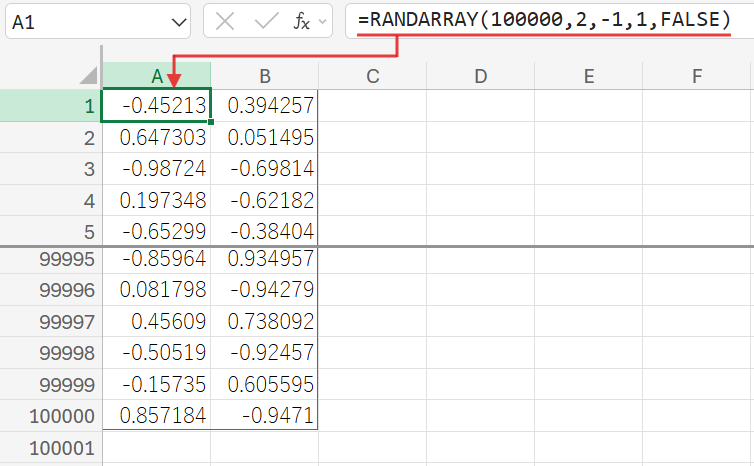
この数式は、「10万行×2列」の範囲に、「-1から1まで」のランダムな小数点以下の数値を生成します。これが、正方形の中に打たれる10万個の点のX座標（A列）とY座標（B列）になります。
STEP2: 複素数とIMABSで原点からの距離を測る
次に、C1セルに以下の数式を入力し、10万行目までオートフィルでコピーします。
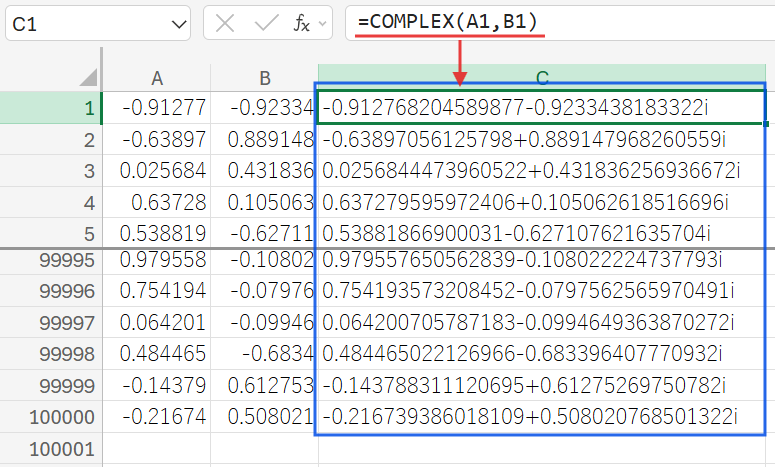
=COMPLEX(A1,B1)
COMPLEX(実数, 虚数): a+biの形の複素数（文字列）を生成します。
これは、X座標A1とY座標B1を、複素数平面上の点として表現するための準備です。
続いて、D1セルに以下の数式を入力し、こちらも10万行目までコピーします。
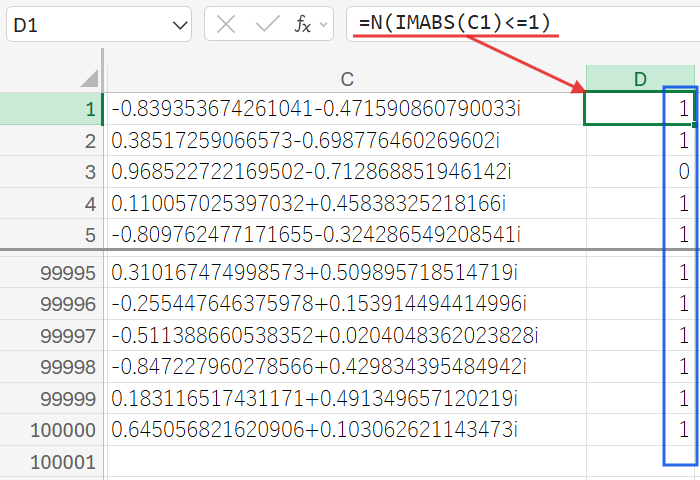
=N(IMABS(C1)<=1)
IMABS(複素数): 複素数の絶対値を返します。複素数平面において、これは原点(0,0)からの距離を意味します。
N(論理値): TRUEを1に、FALSEを0に変換します。
この数式は、「原点からの距離が1以下（つまり、円の内側にある）なら1を、そうでなければ0を返す」という、見事な判定を行っています。
STEP3: AVERAGEで確率を求め、4倍する！
さあ、仕上げです。任意のセル（例えばF1セル）に、以下の数式を入力します。
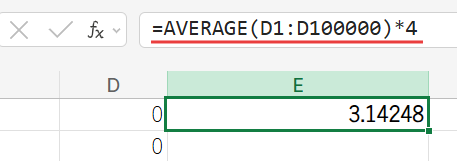
=AVERAGE(D1:D100000)*4
AVERAGE(D1:D100000)の部分は、D列の1と0の平均値を計算します。これは、円の内側に入った点の割合と全く同じ意味になります。
そして、その結果を4倍することで、円周率πの近似値が算出されるのです！
10万行の試行では、だいたい3.13から3.15あたりの値になることが多いようです。
あなたのExcelでは、どんな結果になりましたか？
もしPCの性能に余裕があれば、ぜひRANDARRAYの行数を100万行に増やして、さらに精度を高める挑戦をしてみてください！
まとめ
今回は、PI関数を禁止するという縛りの中で、歴史的な数学の公式「ライプニッツ級数」と、確率統計的なアプローチ「モンテカルロ法」という、全く異なる二つの方法で円周率の近似値を求める、壮大な「暇つぶし」に挑戦しました。
数式を組み立てる過程で、SEQUENCE関数の柔軟な使い方や、RANDARRAYと複素数関数の強力な連携など、Excelの新たな可能性を発見できたのではないでしょうか。
答えを知っているだけの状態から、その答えにたどり着くまでの「プロセス」を、自分の手で再現してみること。
それこそが、私たちの知的好奇心を満たし、Excelへの理解を深めてくれる、最高のスパイスなのです。
あなたのExcelライフが、また一つ、楽しいものになったなら幸いです！
