本記事では、OSを問わず誰でも無料で利用できる「Web版Excel」を使用して検証および画像の作成を行っています。ローカルのExcelをお持ちでないMacやLinuxユーザーの方も、ブラウザさえあれば一緒に挑戦できますよ！
偏差値とは？Excelで計算しながらその「正体」を暴く、大人の自由研究！
「あなたの偏差値は58です」「偏差値70の〇〇大学は難関だ」…。
私たちは昔から、この「偏差値」という言葉を、何か絶対的な「ものさし」のように聞いてきましたよね。
50がちょうど真ん中で、70を超えるとすごく頭が良い…。
そんな漠然としたイメージはあっても、「じゃあ、偏差値って一体どうやって計算されているの？」と聞かれると、意外と知らない方が多いのではないでしょうか。
今回の「Excelで暇つぶし」は、この謎に満ちた「偏差値」の正体を、Excelを使って計算過程を一つずつ追いながら、その本質的な意味までを解き明かす、大人の自由研究です！
この記事を読み終える頃には、あなたは偏差値の計算方法をマスターしているだけでなく、なぜ同じ80点でも、テストによって価値が全く違うのか、その理由を論理的に説明できるようになっているはずです！
STEP1：準備 – 分析データの用意と「見える化」
まずは、今回の自由研究で使う「実験道具」を準備しましょう。
サンプルデータの準備
今回は、20人の生徒が受けた「国語」「数学」「英語」のテスト結果という想定で、以下のような表を用意しました。
excel_de_himatsubushi063.xlsx (WEB版のExcelファイルを開きます)
Excelの便利機能「カラースケール」で、ばらつきを「見る」
計算を始める前に、Excelの便利機能で、データの「ばらつき」を視覚的に捉えてみましょう。
例えば、国語の点数（B2:B21）を選択し、「ホーム」タブ → 「条件付き書式」 → 「データバー」を選んでみてください。
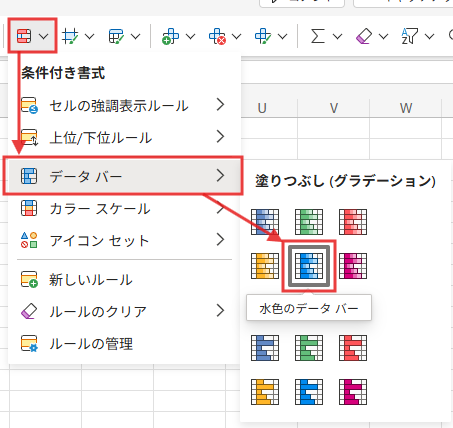
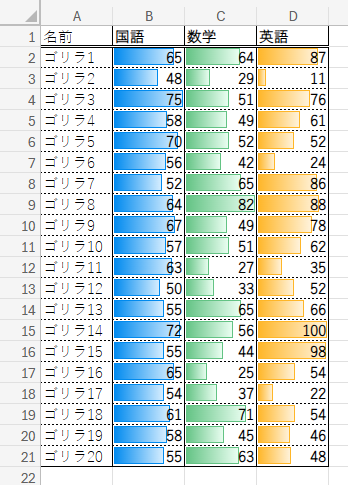
すると、点数が高いほどバーが長く、低いほど短くなるように表示されます。
これを3教科すべてに行うと、それぞれの教科の点数の「ばらつき具合」が、なんとなく見た目で比較できますね。
この「ばらつき」こそが、偏差値を計算する上で非常に重要な要素となるのです。
STEP2：偏差値の計算手順をExcelで追体験する！
さあ、いよいよ計算のステップです。
ここからは、「国語」の点数を例に、偏差値を算出する6つの手順を一つずつ見ていきましょう。
手順1：平均点を出す
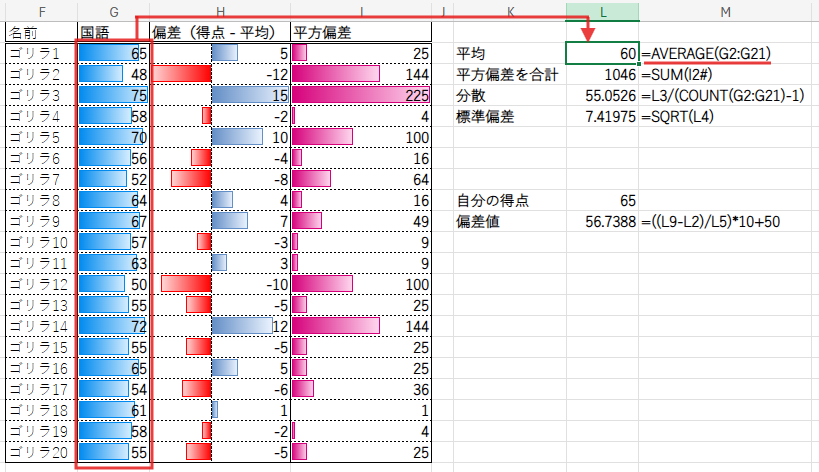
まずは、全体の基準となる「平均点」を計算します。これは簡単ですね。AVERAGE関数を使います。
=AVERAGE(G2:G21)
国語の平均点は「60点」となりました。
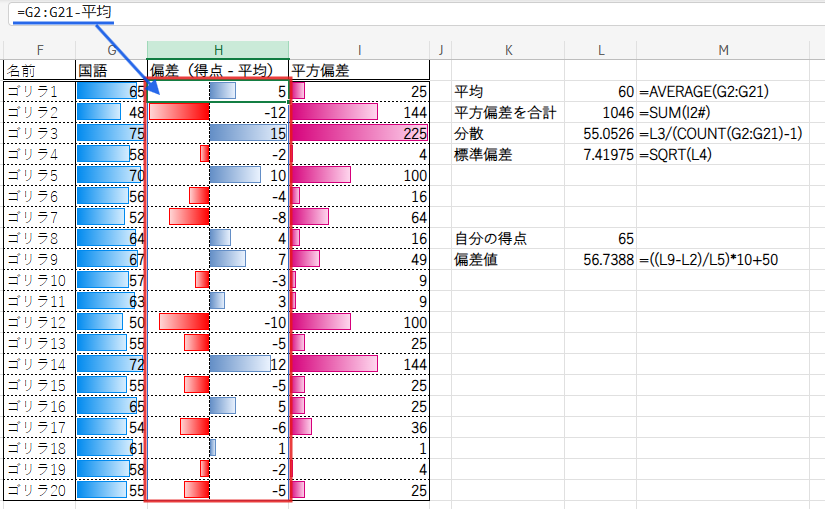
手順2：偏差（得点 – 平均点）を出す
次に、一人ひとりの得点が、平均点からどれだけ離れているかを示す「偏差」を計算します。
=G2:G21-L2
（L2セルに平均点が入っているとします。分かりやすいように名前をつけています。）
Web版Excelなら、この数式だけで20人分の偏差が一気に計算されます（スピル機能）。
平均点より高ければプラス、低ければマイナスになりますね。
手順3：平方偏差（偏差の2乗）を出す
「なぜ、わざわざ2乗するの？なんだか面倒くさい…」
良い質問です！偏差を2乗するのには、2つの明確で重要な理由があります。
- マイナスを消すため: 偏差にはプラスの値とマイナスの値が混在しています。
もしこのまま合計してしまうと、互いに打ち消し合ってしまい、全体のばらつきが正しく測れません。
そこで、2乗して全ての値を正の数に揃えるのです。 - 差を強調するため: 2乗することで、平均から大きく離れている値（外れ値）ほど、より大きな数値になります。
これにより、全体のばらつきを計算する際に、平均から大きく外れた点数の影響がより強く反映されるようになります。
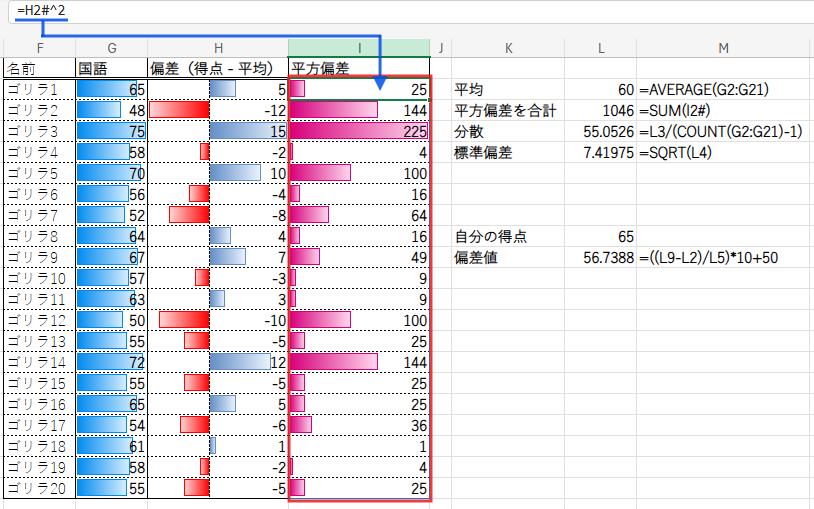
それでは、各偏差を2乗して「平方偏差」を計算しましょう。
=H2#^2
（H2#は、手順2で計算した偏差のスピル範囲を指します）
手順4：分散を出す（平方偏差の平均）
次に、全員の平方偏差を合計し、その平均値を求めます。
この「平方偏差の平均値」こそが、統計学で「分散」と呼ばれる、データ全体のばらつき具合を示す最も基本的な指標です。
分散とは？
データ一つ一つが、平均からどれだけ離れているか（偏差）を2乗した値（平方偏差）の、そのまた平均値です。
つまり、「データ全体の散らばり具合を、平均的な一つの数値で表したもの」と理解してください。分散が大きいほど、データは広く散らばっていると言えます。
まずは、平方偏差を合計します。
=SUM(I2#)
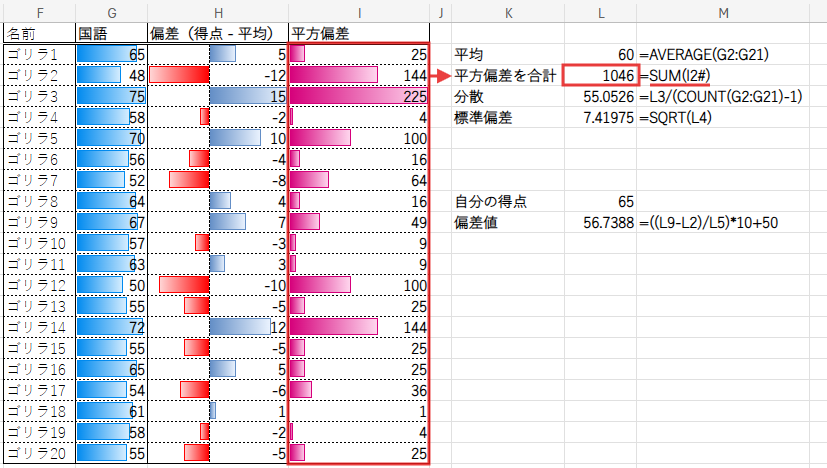
そして、この合計値を人数（から1を引いた数）で割ることで、分散を求めます。
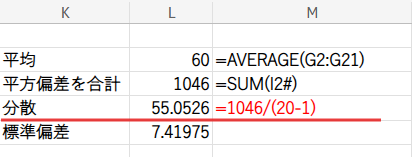
なぜ1を引くのかは、次のステップで詳しく解説します！
手順5：標準偏差を出す
「分散でばらつきが分かったのに、なぜまた別の指標が必要なの？」
それは、分散が「偏差を2乗した値」の平均だからです。
例えば、点数の単位が「点」だとすると、分散の単位は「点²（点二乗）」という、直感的に分かりにくい単位になってしまっています。
そこで、分散の平方根（ルート）をとることで、単位を元の「点」に戻し、より直感的に「平均点から、だいたい何点くらい離れているか」を分かりやすくした指標。それが「標準偏差」です。
計算式は以下の通りです。
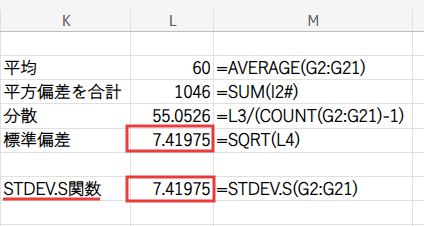
=SQRT(L4)
（L4に分散が入っているとします）
【重要解説】なぜ「-1」するのか？ STDEV.PとSTDEV.Sの違い
「やっぱり気になる！なんで人数（COUNT(B2:B21)）から1を引いて割るの？」
この-1こそ、統計学における非常に重要で、多くの人が疑問に思うポイントです！
Excelには、標準偏差を計算する関数としてSTDEV.PとSTDEV.Sの2種類があります。
- STDEV.P (Population): Pは「母集団」のP。分析したいデータの「全て」が手元にある場合に使います。分母はデータの個数nです。
- STDEV.S (Sample): Sは「標本」のS。手元にあるデータが、より大きな集団から抜き出した一部（サンプル）である場合に使います。分母はデータの個数-1、つまりn-1です。
なぜ標本の場合はn-1で割るのでしょうか？
非常に厳密な数学的証明は省きますが、ざっくり言うと、「一部のサンプルデータだけを使って計算した『ばらつき』は、母集団全体の本当の『ばらつき』よりも、少し小さめに見積もられてしまう傾向があるから」です。
そのため、分母を少しだけ小さく（n-1に）することで、計算結果を少しだけ大きくし、より「母集団全体のばらつきに近いであろう、より正確な推定値」に補正しているのです。
今回の「20人の生徒」は、学年全体や全国の受験生といった、より大きな母集団からの一部（標本）と考えるのが自然ですよね。なので、n-1で割るSTDEV.Sと同じ計算をしています。
実際に、手計算の結果と、=STDEV.S(G2:G21)の結果が一致することを、ぜひ確かめてみてください！
手順6：偏差値を出す！
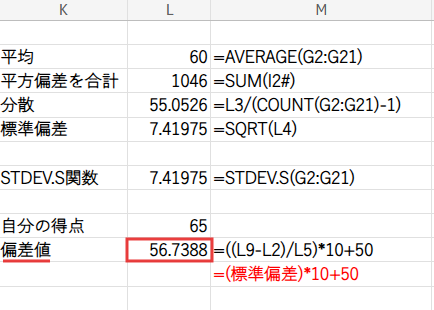
さあ、全ての部品が揃いました！いよいよ偏差値を計算します。
偏差値とは、「平均点が50、標準偏差が10になるように、自分の点数を変換したもの」です。
数式はこうなります。
=((L9-L2)/L5)*10+50
(L9-L2)/L5)の部分は、自分の偏差が標準偏差の何倍あるか（基準化）を計算しています。
偏差値＝((自分の得点－平均点)÷標準偏差)×10＋50
それに10を掛けて50を足すことで、平均50、標準偏差10のスケールに変換しているのです。
STEP3：偏差値の本質 – 「平均点」と「ばらつき」が価値を決める
さて、同じ手順で、数学と英語の偏差値も計算してみましょう。
ここで、ある生徒の点数に注目します。ファイルにも入力されていますが、「自分の得点」を65点としましょう。
もし、国語、数学、英語の3教科で、たまたま全て65点を取ったとしたら、偏差値も全て同じになるでしょうか？
「え、同じ点数なんだから、同じ偏差値になるんじゃないの？」
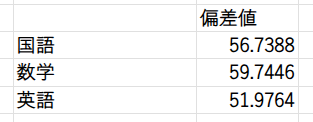
答えは「NO」です！実際に計算した結果を見てみましょう。
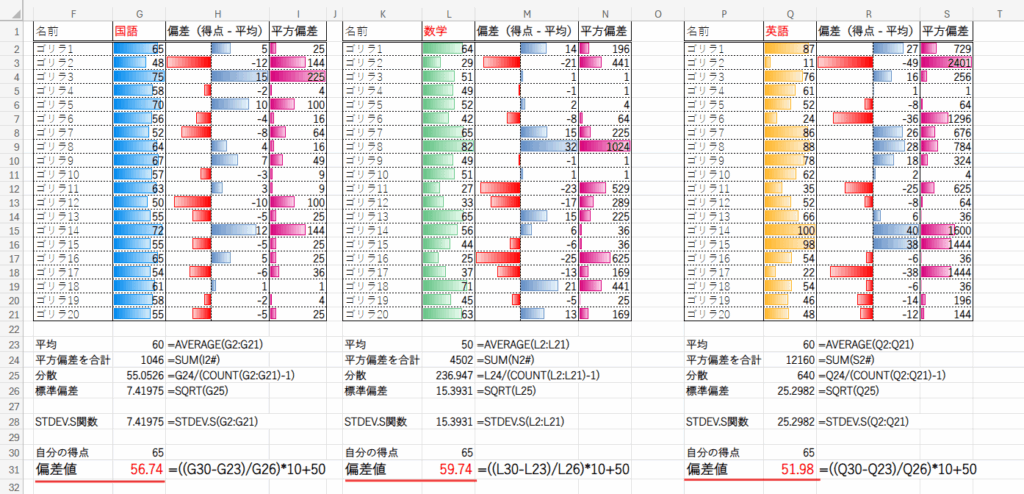
驚きましたか？
同じ65点でも、数学では偏差値が59.74と最も高く、英語では51.98と最も低くなっています。
国語と英語は平均点が同じ60点なのに、偏差値が違いますね。
この違いを生んでいるのが、偏差、つまり「点数のばらつき」なのです。
- 英語は標準偏差が25.29と非常に大きく、点数が広くばらついています。
このような「実力差がはっきりした」テストでは、平均より少し高い65点を取っても、それほど抜きん出た存在にはなれず、偏差値は低めになります。 - 逆に国語は標準偏差が7.42と小さく、ほとんどの人が平均点近くに固まっている「団子状態」のテストです。
このような中で平均より5点高い65点を取ることは、相対的に価値が高く、偏差値も高くなります。
つまり、平均点が高いテストで80点を取るより、平均点が低いテストで80点を取る方が偏差値は高くなります。
そして、皆が同じような点を取るテスト（標準偏差が小さい）で高得点を取る方が、点数がばらけているテスト（標準偏差が大きい）で同じ点を取るよりも、偏差値は高くなるのです。
偏差値とは、単なる点数ではなく、その集団の中での「相対的な位置」を示す、非常に優れた指標なのですね。
まとめ
今回は、「偏差値」という身近なテーマを、Excelを使ってその計算過程から本質的な意味まで、一歩ずつ丁寧に解き明かしていきました。
平均、偏差、分散、標準偏差…。
これらの統計学の基本的な概念が、いかにして「偏差値」という一つの指標に集約されていくか、その美しいプロセスを体感していただけたのではないでしょうか。
そして、STDEV.PとSTDEV.Sの違い（なぜn-1で割るのか？）や、同じ点数でもテストの「ばらつき」によって価値が変わるという、偏差値の真の意味もご理解いただけたかと思います。
この「暇つぶし」が、あなたの日常にある「数字」の裏側を見る、新しい視点をもたらすきっかけになれば、これほど嬉しいことはありません。
