本記事では、無料のWeb版Excelを使用して検証および画像の作成を行っています。Windowsはもちろん、MacやLinuxの方もブラウザさえあれば挑戦できます！
はじめに：1つの数式が、2つの答えを導く！？
Excelで数式を入力すると、通常、答えは1つのセルに表示されます。
これは、長年のExcelユーザーにとっては「常識」でした。
しかし、現代のExcelには、その常識を覆す「スピル」という画期的な機能が備わっています。
スピルとは、たった一つの数式が、複数のセルにわたって複数の結果を自動的に展開（溢れ出させる）する現象のことです。
「え、一つの数式で複数の計算を同時に？
まるで分身の術みたいだけど、一体どういう仕組みなの？」
今回の記事は、この「スピル」の力を最大限に引き出す、思考のパズルです。
「60点以上の人数」と「60点未満の人数」という、2つの異なる集計を、たった一つの数式で同時に行い、2つのセルにスピルさせて表示させるテクニックに挑戦します。
この挑戦を通して、スピルの核心である「配列定数」の扱いや、長年その真価を隠し続けてきた「FREQUENCY関数」の驚くべき実力に迫ります。
さあ、あなたのExcelの世界観をアップデートする、新たな扉を開きましょう！
今回のミッション
現在の状態： まず、社員のテスト結果が書かれたシンプルなリストがシートにあります。
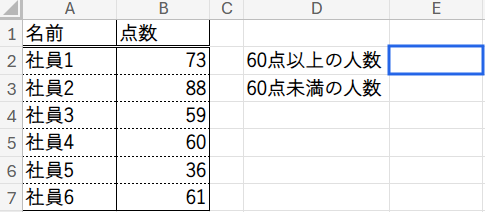
目指すゴール： D列の「60点以上の人数」「60点未満の人数」という2つの項目を、E2セルに入力するたった一つの数式で計算し、E2セルとE3セルにスピルさせて表示させます。
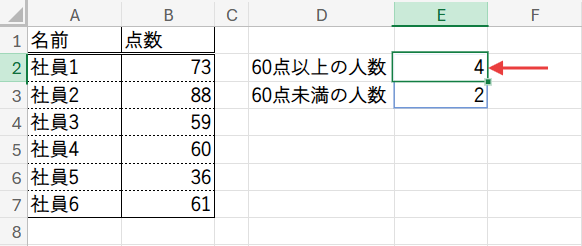
ルール：
- 結果は、E2セルに入力する1つの数式で求めること。
- 計算のための作業列は一切使用しないこと。
アプローチ1：COUNTIF + 配列定数（最もシンプルな正攻法）
考えかた
最初に紹介するのは、最もシンプルで直感的な方法です。
通常、COUNTIF関数は =COUNTIF(B2:B7, ">=60") のように、一つの条件で一つの結果を返します。
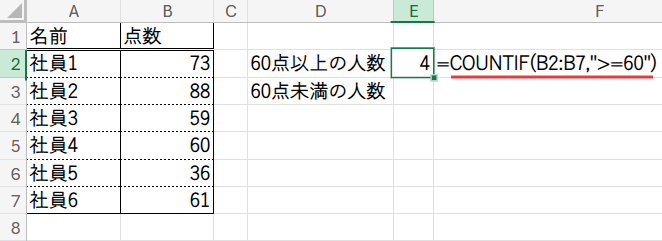
しかし、この第2引数（検索条件）に、「配列定数」というささやかな魔法をかけることで、COUNTIF関数は一度に複数の条件を処理し、複数の結果を返すようになります。
「60点以上」と「60点未満」という2つの条件を配列定数として渡してあげることで、一回の命令で2つの答えを同時に計算させるのです。
数式と解説
E2セルに、以下の数式を入力します。
=COUNTIF(B2:B7,{“>=60″;”<60”})
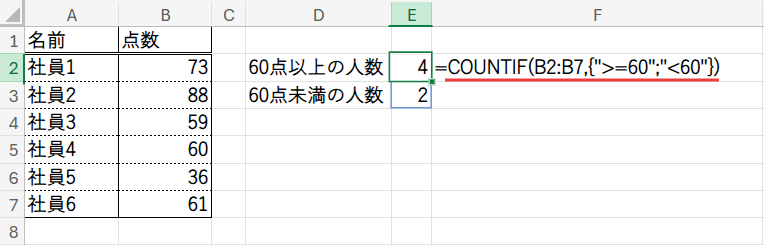
見事に2つの結果が表示されましたね。
この数式の心臓部は、波括弧 { } で囲まれた {">=60";"<60"} の部分です。
これが「配列定数」と呼ばれるもので、数式の中に直接、値の配列を書き込むための記法です。
ここで重要なのが、値を区切る記号です。
- カンマ
,で区切る →{1,2,3}→ 横方向の配列（行） - セミコロン
;で区切る →{1;2;3}→ 縦方向の配列（列）
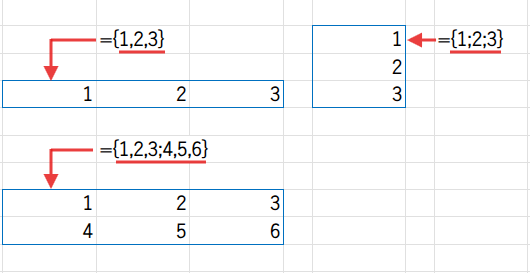
今回はセミコロン ; を使っているので、Excelは「”>=60″」と「”<60″」という2つの条件を「縦に並んだ配列」として認識します。
そして、COUNTIF関数は、この2つの条件を上から順番に処理します。
- まず、範囲B2:B7に対して1つ目の条件「”>=60″」で計算し、「4」という結果を得ます。
- 次に、範囲B2:B7に対して2つ目の条件「”<60″」で計算し、「2」という結果を得ます。
最終的に、Excelは {4;2} という縦方向の配列を生成し、これをE2セルから下方向へスピルさせて表示する、というわけです。
このように、引数に配列定数を与えるだけで、普段は一つの答えしか返さない関数に複数の仕事をさせることができるのです。
アプローチ2：IF + 配列定数（いにしえの強制実行テクニック）
考えかた
次に紹介するのは、配列数式を古くから使っているユーザーにはお馴染みの、少し変わったテクニックです。
IF関数は通常、IF(条件, 真の場合, 偽の場合) のように、条件が真か偽かによってどちらか一方の処理しか行いません。
しかし、この第1引数（条件）に {1;0} という配列定数を渡すと、挙動が変化します。
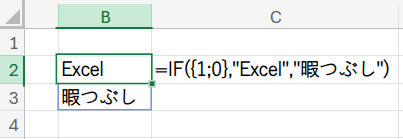
これはExcelに「1番目（真の場合）の処理と、2番目（偽の場合）の処理を、両方とも強制的に実行しなさい」と命令しているようなものです。
このテクニックは、かつてVLOOKUP関数で参照範囲の左側の列を取得する、といった高度な使い方でも応用されていました。
こちらの記事で紹介しています。
今回は、この性質を利用して、「60点以上の合計（人数）」と「60点未満の合計（人数）」を同時に計算させます。
数式と解説
E2セルに、以下の数式を入力します。
=IF({1;0},SUM(N(B2:B7>=60)),SUM(N(B2:B7<60)))
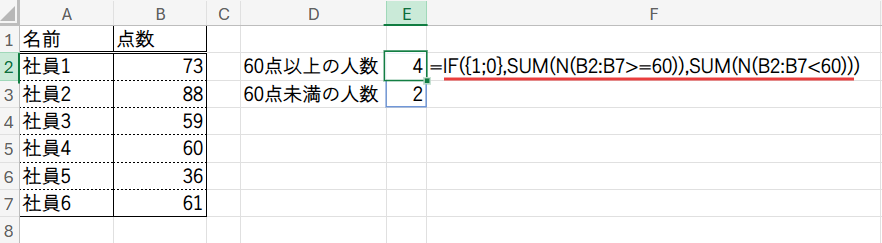
この数式も、内側のロジックから見ていきましょう。
Step 1: N(B2:B7>=60) – 論理値を数値に変換する
まず、B2:B7>=60 の部分です。
これは、B2からB7の各セルが60以上かどうかを判定し、{TRUE;TRUE;FALSE;TRUE;FALSE;TRUE} のような論理値（TRUE/FALSE）の配列を返します。
しかし、このままではSUM関数で合計できません。
そこで登場するのがN関数です。
N関数は、引数の値を数値に変換しようと試みる関数で、TRUEは「1」に、FALSEは「0」に変換してくれる性質があります。
この結果、{1;1;0;1;0;1} という数値の配列が出来上がります。
ちなみに、この論理値の数値化は、他にも (B2:B7>=60)*1 や --(B2:B7>=60) のような演算子を使った方法でも実現できます。
N関数は、その意図が分かりやすいというメリットがあります。
Step 2: SUM(...) – それぞれの人数を合計する
Step1で作成した {1;1;0;1;0;1} という配列を、SUM関数で合計します。
結果はもちろん「4」となり、これが「60点以上の人数」です。
同様に、SUM(N(B2:B7<60)) の方も計算され、「2」という「60点未満の人数」が求められます。
Step 3: IF({1;0}, ... , ...) – 2つの結果を配列にまとめる
最後に、IF関数がこれらの結果をまとめ上げます。
IF({1;0}, 4, 2) という形になり、Excelはこれを {4;2} という縦方向の配列として解釈し、セルにスピルさせます。
こうして、2つの異なるSUM計算の結果を、一つの数式で得ることができました。
アプローチ3：MMULT（行列の積で無理やり計算！？）
考えかた
3つ目は、完全に「関数パズル」としての遊び心から生まれた、超絶技巧です。
MMULT関数は、本来、数学の「行列の積」を計算するための専門的な関数です。
これを、どうにかして今回の「人数のカウント」に応用してしまおう、という無茶な試みです。
ロジックは非常に難解ですが、「こんなことまでできるのか！」というExcelの懐の深さを感じられるはずです。
数式と解説
E2セルに、以下の数式を入力します。
=TRANSPOSE(MMULT(SIGN(COLUMN(INDIRECT(“A1:”&ADDRESS(1,COUNTA(A2:A7))))),N(INT(B2:B7/60)={1,0})))
もはや何かの暗号ですね。
この数式を理解するには、「行列の積」の基本ルールを知る必要があります。
(A行 x B列) の行列と (B行 x C列) の行列を掛け合わせると、(A行 x C列) の行列が生まれます。
この性質を巧みに利用しています。
Step 1: N(INT(B2:B7/60)={1,0}) – 2次元の判定配列を作る
数式の核となる、非常に面白い部分です。
まず、INT(B2:B7/60) が、各点数を60で割った商の整数部分を計算します。
- 60点以上（例: 73, 88, 60, 61）→ 商は「1」
- 60点未満（例: 59, 36）→ 商は「0」
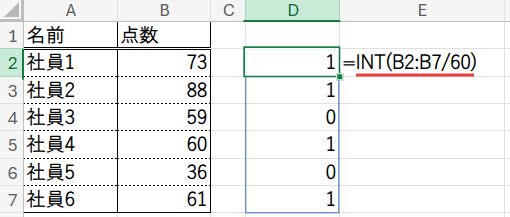
この結果の配列 {1;1;0;1;0;1} を、配列定数 {1,0} と比較します。
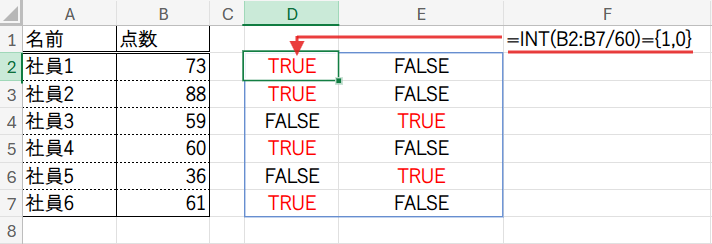
すると、Excelはそれぞれの要素を比較した、6行x2列の巨大な論理値の配列を生成します。
これをN関数で数値化すると、[1,0; 1,0; 0,1; 1,0; 0,1; 1,0] という形の、6行2列の行列が完成します。
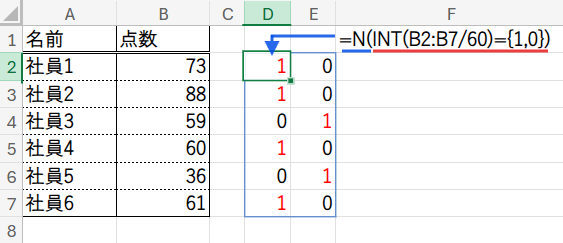
Step 2: SIGN(COLUMN(INDIRECT(...))) – すべてが「1」の行列を作る
次に、掛け合わせるための、もう一方の行列を作ります。
ここは、すべてが「1」で構成された、1行6列の行列を作ることが目的です。
COUNTA(A2:A7)でデータ数「6」を取得し、ADDRESSとINDIRECTで「A1:F1」というセル範囲を作り、COLUMNで{1,2,3,4,5,6}という配列を得ます。
最後にSIGN関数（数値の符号を返す関数。正の数は1になる）を使い、すべてを「1」に変換しています。
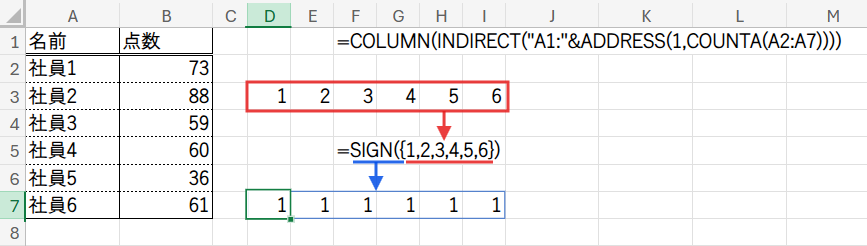
Step 3: MMULT(...) と TRANSPOSE(...) – 行列計算と仕上げ
いよいよMMULT関数で、Step2の (1×6)行列 と Step1の (6×2)行列 を掛け合わせます。
ルール通り、結果は (1×2)行列、つまり {4, 2} のような横方向の配列になります。
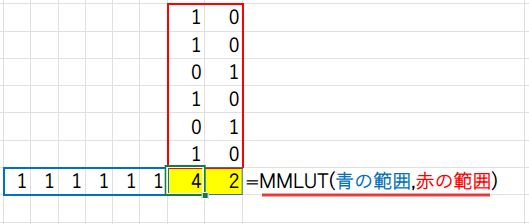
しかし、スピルさせるには縦方向の配列が必要です。
そこで、最後の仕上げにTRANSPOSE関数（行と列を入れ替える関数）を使い、{4,2} を {4;2} という縦配列に変換して、見事ゴールとなります。
アプローチ4：FREQUENCY + INDEX（眠れる獅子、覚醒）
考えかた
さて、ここからが今回の本番です。
主役はFREQUENCY関数。その名の通り「頻度」や「分布」を調べるための関数です。
こちらの記事でも紹介しています。
この関数は、指定した「区切り点（区間）」ごとに、データがいくつあるかを一発で計算してくれます。
今回は「59点」を区切り点として指定します。
すると、「59点以下のグループ」と「59点より大きいグループ」の2つの人数を同時に計算してくれます。
ただし、この関数には少しクセがあり、結果の並び順を工夫する必要があります。
数式と解説
E2セルに、以下の数式を入力します。
=INDEX(FREQUENCY(B2:B7,59),{2;1})
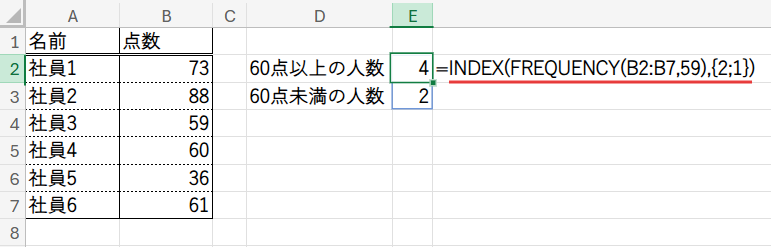
Step 1: FREQUENCY(B2:B7,59) – 区切り点を使って人数を数える
まず、FREQUENCY関数の基本を理解しましょう。
FREQUENCY(データ範囲, 区間配列) という形で使います。
「区間配列」に指定した数値が「区切り点」となり、それ以下のグループにデータが分類されます。
今回は区切り点として「59」を一つだけ指定しました。
すると、FREQUENCY関数は以下の2つのグループの人数を数えます。
- 59以下のデータの個数
- 59より大きいデータの個数
そして、結果を {2;4} という配列で返します。1番目が「59以下（60未満）」の人数、2番目が「59より大きい（60以上）」の人数です。
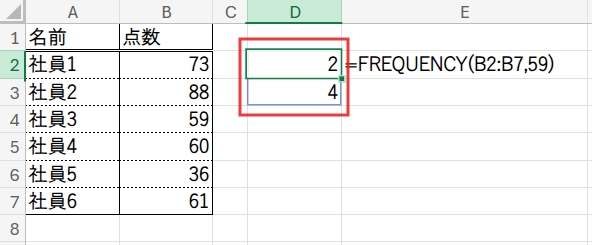
なぜ区切り点を「60」ではなく「59」にするのか？ もし「60」にしてしまうと、「60以下のグループ」となり、60点が60点未満のグループに含まれてしまうためです。
これがFREQUENCY関数を使う上での重要なポイントです。
Step 2: INDEX(...,{2;1}) – 結果の順番を入れ替える
Step1で得られた結果は {2;4} でした。
これは「60点未満」が上で、「60点以上」が下になっています。
私たちが表示したい順番は逆ですよね。
そこで、INDEX関数と配列定数を使って、この結果の順番を入れ替えます。
INDEX({2;4}, {2;1}) という形になります。
これは、INDEX関数に「まず配列の2番目の要素（4）を持ってきて、次に1番目の要素（2）を持ってきなさい」と命令しているのと同じです。
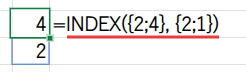
結果として、{4;2} という、望み通りの順番の配列が生成され、セルにスピルします。
アプローチ5：FREQUENCY + LOOKUP（データを変換してから数える）
考えかた
先ほどは、計算結果の「順番を入れ替える」という後処理を行いました。
今度は逆の発想です。
「計算する前に、データを都合の良い形に変換してしまえばいいのでは？」
ここでは、LOOKUP関数を使って、元の点数データを「60点以上なら0」「60点未満なら1」という、2種類のシンプルな数値に変換します。
この変換済みのデータをFREQUENCY関数で集計することで、後処理なしで直接答えを導きます。
数式と解説
E2セルに、以下の数式を入力します。
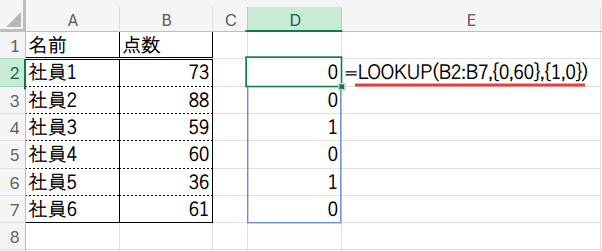
=FREQUENCY(LOOKUP(B2:B7,{0,60},{1,0}),0)
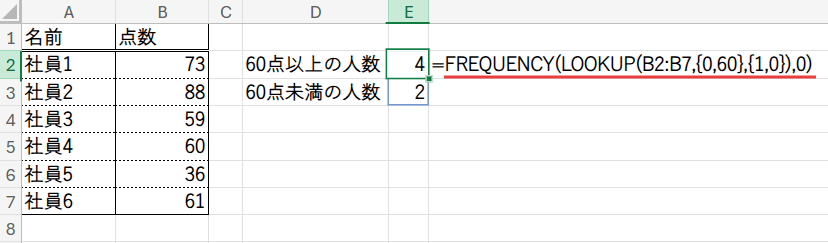
Step 1: LOOKUP(B2:B7,{0,60},{1,0}) – 点数を「0」と「1」に変換
この数式の主役、LOOKUP関数の登場です。
LOOKUP関数については以下の記事でも紹介しています。
LOOKUP(検索値, 検索範囲, 対応範囲) という形で使います。
ここでは、検索範囲に{0,60}、対応範囲に{1,0}という配列定数を指定しています。
これは、以下のようにデータを変換する命令になります。
- 点数が0以上60未満の場合 → 対応する「1」を返す
- 点数が60以上の場合 → 対応する「0」を返す
この処理により、元の点数配列は {0;0;1;0;1;0} という、0と1だけで構成された新しい配列に変換されます。
Step 2: FREQUENCY(...,0) – 0と1の個数を数える
次に、この変換された配列をFREQUENCY関数に渡します。
今回は、区切り点として「0」を指定します。
すると、以下の2つのグループの人数を数えます。
- 0以下のデータ（つまり「0」）の個数
- 0より大きいデータ（つまり「1」）の個数
結果として、{4;2} という配列が直接生成されます。
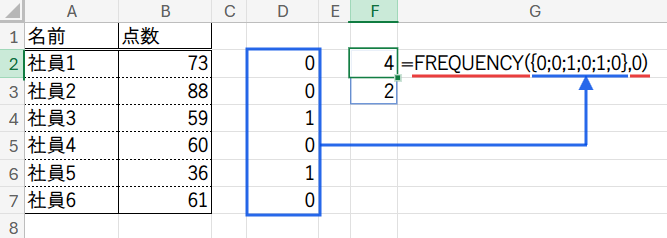
これは「0の個数（＝60点以上の人数）」と「1の個数（＝60点未満の人数）」を意味しており、望む通りの順番になっていますね。
アプローチ6：FREQUENCY + 負の数（究極の裏ワザハック）
考えかた
最後は、配列定数すら使わずにスピルを実現する、究極の裏ワザです。
「もし、すべての数値をマイナスにしてしまったら？」という、常識を疑う発想から生まれています。
数値の大小関係が逆転することを利用し、FREQUENCY関数の区切り点の仕様を逆手に取る、非常に面白い方法です。
ただし、この方法は「元のデータがすべて正の整数である」という前提があって初めて成り立ちます。
数式と解説
E2セルに、以下の数式を入力します。
=FREQUENCY(B2:B7*-1,-60)
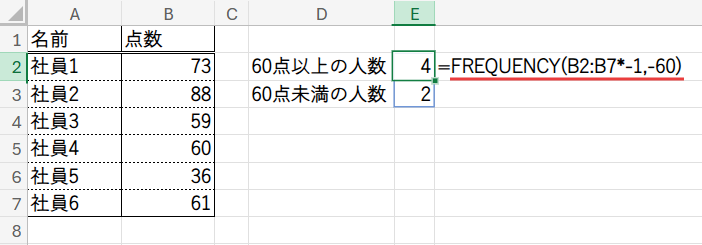
驚くほど短いですね。
この数式は、2つのステップで動いています。
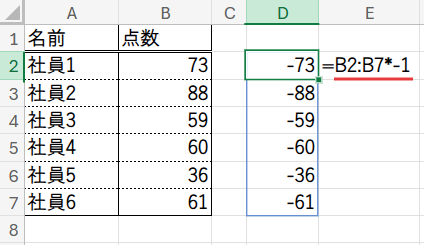
Step 1: B2:B7*-1 – すべての点数を負の数に変換
まず、データ範囲B2:B7のすべての点数に「-1」を掛け合わせます。
これにより、すべての点数がマイナスの値に変換されます。（例: 73 → -73, 59 → -59）
Step 2: FREQUENCY(...,-60) – 負の区切り点でカウント
次に、このマイナスの点数配列を、区切り点「-60」で分類します。
FREQUENCY関数のルールに従うと、以下の2つのグループができます。
- -60以下のデータの個数
- -60より大きいデータの個数
ここで、よく考えてみてください。
負の世界では、数値が小さいほど絶対値は大きくなります。
つまり、「-60以下」（例: -60, -73, -88）というのは、元の世界では「60以上」だった数値たちです。
同様に、「-60より大きい」（例: -59, -36）というのは、元の世界では「60未満」だった数値たちです。
結果として、FREQUENCY関数は、私たちが望む通りの順番で「60点以上の人数」と「60点未満の人数」を計算し、{4;2}という配列を直接返してくれるのです。
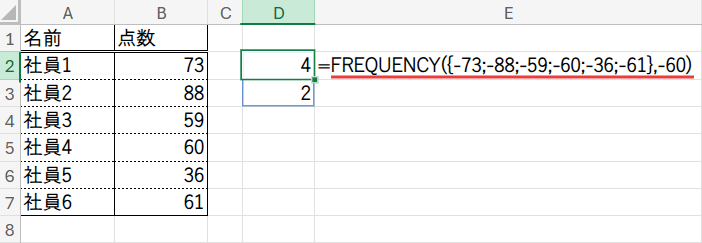
まさに、発想の勝利と言えるでしょう。
まとめ：スピルが解き放った、FREQUENCY関数の真価
今回は、「2つの異なる条件のカウントを、1つの数式でスピルさせる」というテーマで、6つのアプローチを探求しました。
特に、後半の3つのアプローチで主役となったFREQUENCY関数。
この関数は、実はExcelのかなり古いバージョンから存在する、由緒ある関数です。
しかし、スピル機能がなかった時代（Excel 2019以前）、この関数を使うには、あらかじめ結果が表示されるセル範囲（今回は2つのセル）を選択した状態で数式を入力し、最後にCtrl + Shift + Enterで配列数式として確定させる必要がありました。
この手順が非常に分かりにくく、少し扱いにくい関数という印象を持たれ、あまり活用されてこなかったかもしれません。
しかし、時代は変わりました。
FREQUENCY関数は、まるで「スピル」という機能の登場を、ずっと待ち続けていたかのようでした。
スピル機能のおかげで、面倒な事前選択やCSE確定は一切不要になり、計算結果は自動で表示されます。
互換性は抜群で、LOOKUP関数のように区切り点で条件を指定できるため、ロジックの可読性も高い。
眠れる獅子が、ついにその真価を発揮する時が来たのです。
今回の挑戦が、皆さんのExcelの「引き出し」を一つでも多く増やすきっかけになれば、これほど嬉しいことはありません。
- Excel FREQUENCY関数 スピルで覚醒！
- Excel 最頻出文字を求める関数パズル
- Excel FILTER関数の代替案3選！関数パズルに挑戦
- LOOKUP関数の使い方！IFより簡単な条件分岐
- Excelの隠し関数！DATEDIF, EVALUATEを知ってる？
