本記事では、無料のWeb版Excelを使用して検証および画像の作成を行っています。Windowsはもちろん、MacやLinuxの方もブラウザさえあれば挑戦できます！
はじめに：複雑な料金計算、どうしてますか？
遊園地、美術館、イベント会場…。
多くの施設では、年齢によって入場料が変わります。
「幼児は100円、小人は800円、大人は1800円…」といった料金体系は、日常でよく見かける光景ですね。
さて、ある日の来場者リスト（生年月日のみ）を渡されたあなた。
「このリストから、今日の入場料の合計売上を計算してください」
と言われたら、どうしますか？
一人ひとりの年齢を計算し、料金表と見比べて、電卓で合計…なんて、まさかしていませんよね？
今回の記事は、この実務で頻繁に遭遇する「年齢別の料金計算」という課題を、Excel関数を駆使してスマートに解決するためのテクニック集です。
教科書通りの堅実な方法から、知る人ぞ知る便利な関数、そして関数パズルの領域まで、6つの異なるアプローチで「合計売上」というゴールを目指します。
さあ、あなたのExcelスキルをビジネスの現場で輝かせましょう！
今回のミッションと準備
現在の状態：
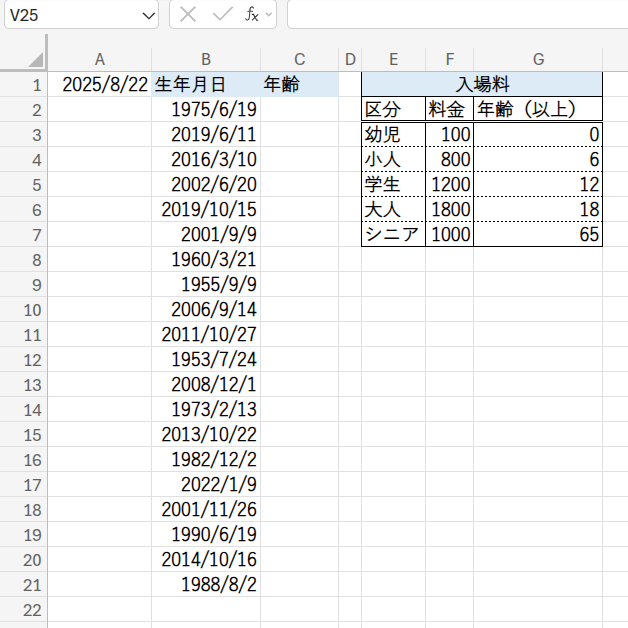
シートには3つの情報が用意されています。
A1セル: 売上を計算する基準日（例：「2025/8/22」）
B2:B21の範囲: 来場者の生年月日リスト
E2:G7の範囲: 年齢区画ごとの料金表
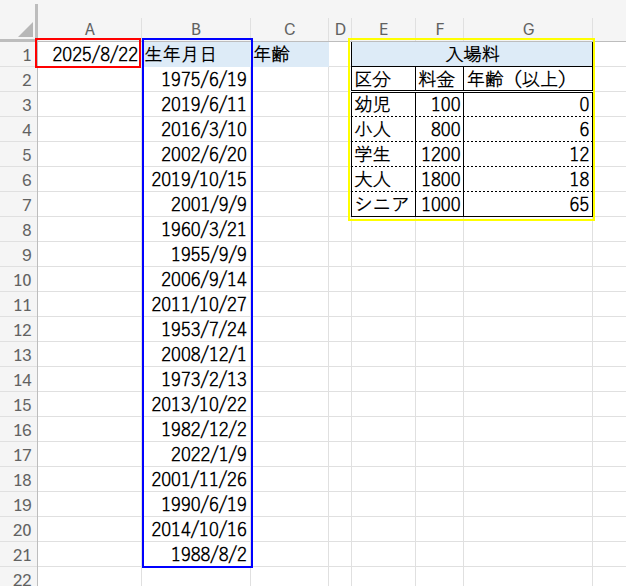
ここで注目してほしいのが、料金表の作りです。
「年齢（以上）」の列が「料金」列の右側にあるため、VLOOKUP関数が使えないようになっています。
目指すゴール：
生年月日リストから各来場者の年齢を計算し、料金表に基づいてそれぞれの入場料を割り当て、その合計金額を、C列「年齢」以外の作業列を使わずに一つの数式で算出します。
準備1：DATEDIF関数で年齢を計算する
まずは、売上の合計を計算する前に、各来場者の「年齢」を計算するところから始めましょう。
今回はC列を作業列として使い、ここに年齢を表示させます。
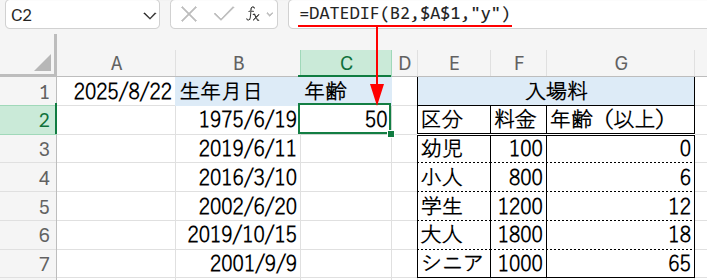
C2セルに、以下の数式を入力します。
=DATEDIF(B2,$A$1,”y”)
DATEDIF関数については以下の記事でも紹介しています。
DATEDIF関数は、2つの日付間の期間を、年数、月数、日数などで計算できる便利な関数です。
- 第1引数 B2: 開始日（生年月日）
- 第2引数 $A$1: 終了日（基準日）。下にコピーしても動かないように絶対参照$A$1にします。
- 第3引数 “y”: “Year“の略。期間を満年数で返す、という意味です。
この数式をC21セルまでフィルコピーすれば、全員の満年齢が計算できます。
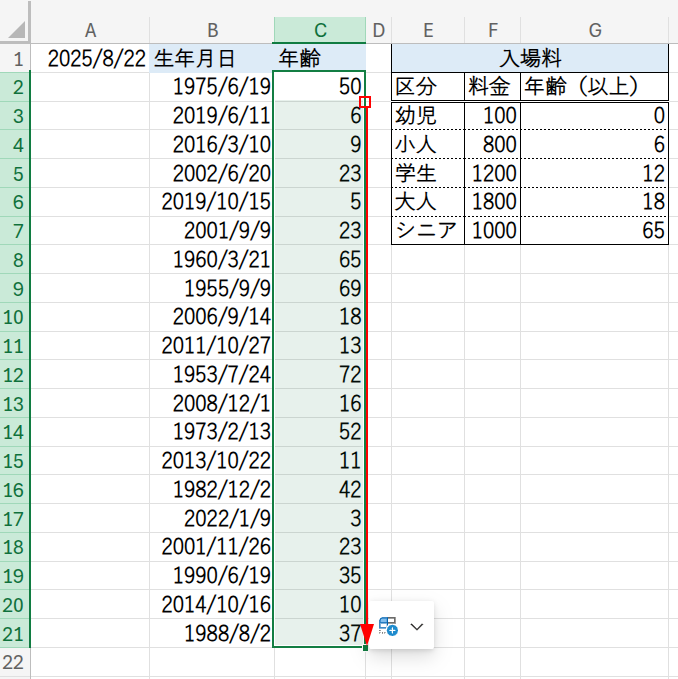
準備2：セル範囲に「名前の定義」をする
今回の数式は少し長くなるものもあるため、可読性を上げるために「名前の定義」という機能を使います。
これは、特定のセル範囲に分かりやすい名前を付けて、数式の中でその名前を使えるようにする機能です。
無料のWeb版Excelでは、リボンの「数式」タブから設定します。
次に、「数式」タブの中にある「ネーム マネージャー」をクリックします。
表示された画面の「+ 新規」ボタンを押します。
「名前」の欄に「年齢」と入力し、「参照先」が正しい範囲になっていることを確認してOKを押します。
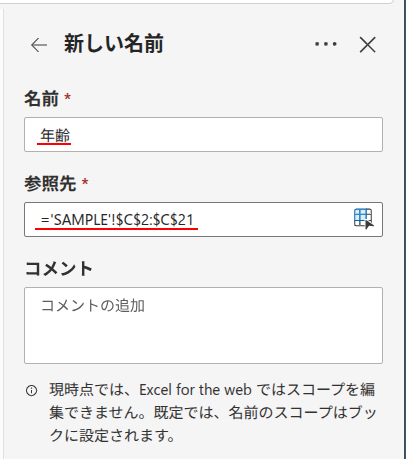
同様の手順で、以下の3つの名前を定義します。
C2:C21の範囲に「年齢」F3:F7に「料金」G3:G7に「区切り」
これで準備は完了です。
それでは、合計金額を求める6つのアプローチを見ていきましょう！
アプローチ1：SUM + IFS（現代の教科書的解法）
考えかた
最初に紹介するのは、複数の条件分岐を簡潔に記述できるIFS関数を使った、現代の教科書的な方法です。
「もし年齢が6歳未満なら100円、もし6歳以上12歳未満なら800円…」という料金表のルールを、そのまま素直に数式に落とし込みます。
この方法で、まず各個人の料金を配列として求め、最後にそれをSUM関数で合計します。
数式と解説
合計金額を表示したいセルに、以下の数式を入力します。
=SUM(IFS(年齢<6,100,年齢<12,800,年齢<18,1200,年齢<65,1800,TRUE,1000))
IFS関数は、IFS(条件1, 真の場合1, 条件2, 真の場合2, ...) という形で、複数の条件を順番に判定していきます。
この数式では、引数に「年齢」という名前を付けた範囲を指定しているため、Excelは20人分の年齢に対して、一括でこの条件判定を行います。
年齢<6,100: まず、年齢が6歳未満か判定。TRUEなら100を返す。
年齢<12,800: 1つ目の条件がFALSEだった人のみ、年齢が12歳未満か判定。TRUEなら800を返す。
…と続き、
TRUE,1000: これまでのどの条件にも当てはまらなかった人（65歳以上）は、最後のこの条件が必ずTRUEになるため、1000を返す。
この結果、20人分それぞれの入場料が並んだ配列（例：{1800;800;800;...}）がメモリ上に生成されます。
最後に、SUM関数がこの配列を合計して、最終的な売上合計を算出します。
【補足】なぜSUMIFSではない？
SUMIFS関数は、既存の範囲を「条件に基づいて合計する」関数です。今回は、まず「年齢に基づいて料金を決定する」という新しいデータ（料金の配列）を作り出す必要があるので、SUMIFSの出番ではありません。
また、条件範囲と合計範囲が異なるため、SUMIFSの構造には当てはまりません。
アプローチ2：SUM + INDEX + MATCH（VLOOKUPが使えない時の王道）
考えかた
次に紹介するのは、VLOOKUP関数が使えない状況で、表からデータを引き出す際の定番コンビ、INDEX関数とMATCH関数を使った方法です。
このアプローチの鍵は、MATCH関数の検索オプションにあります。
通常、完全一致の「0」を使うことが多いですが、今回は近似一致の「1」を使うことで、「●歳以上」という条件をクリアします。
数式と解説
合計金額を表示したいセルに、以下の数式を入力します。
=SUM(INDEX(料金,MATCH(年齢,区切り,1)))
MATCH(年齢,区切り,1): この数式の心臓部です。
MATCH(検索値, 検索範囲, 検索の種類)という形で使います。
- 検索値: 年齢（20人分の年齢の配列）
- 検索範囲: 区切り（料金表の年齢の区切り
{0;6;12;18;65}） - 検索の種類: 1（検索値以下の最大値を検索する。検索範囲は昇順である必要がある）
例えば、年齢が「9歳」の場合、「9」以下の最大値である「6」が「区切り」配列の2番目にあるため、MATCH関数は「2」を返します。
年齢が「50歳」なら、「18」が該当し「4」を返します。
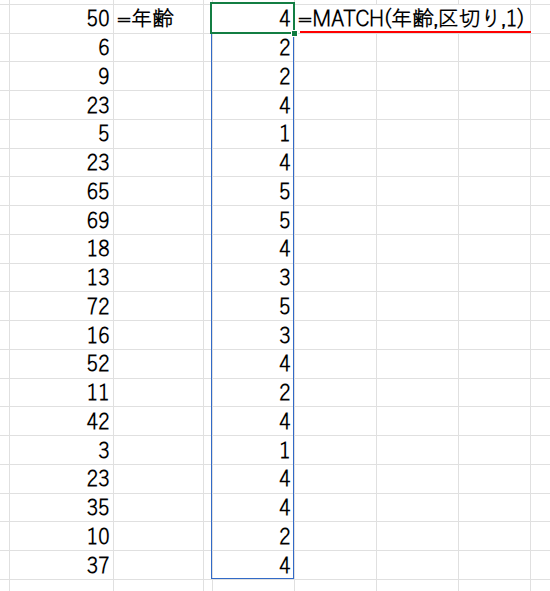
この処理が20人分一括で行われます。
INDEX(料金, …): INDEX関数が、MATCH関数が返した位置番号の配列（例：{4;1;2;...}）を使って、「料金」配列から対応する料金を抜き出します。
位置番号が「2」なら料金配列の2番目「800」が、「4」なら4番目「1800」が返されます。
SUM(…): 最後に、こうして得られた20人分の料金の配列を合計します。
アプローチ3：SUM + LOOKUP（筆者イチオシ！知る人ぞ知る名関数）
考えかた
3つ目は、筆者が個人的に最も美しいと感じる方法、LOOKUP関数です。
LOOKUP関数は、Excelの中でも古株の関数で、一見するとVLOOKUPやHLOOKUPに役目を奪われた時代遅れの関数のようにも見えます。
しかし、今回のような「昇順に並んだ区切り点から、対応する値を取り出す」というタスクにおいては、他のどの関数よりもシンプルで強力な性能を発揮します。
まさに、このケースのために生まれてきたような関数です。
数式と解説
合計金額を表示したいセルに、以下の数式を入力します。
=SUM(LOOKUP(年齢,区切り,料金))
見てください、このシンプルさ！
LOOKUP関数は、LOOKUP(検索値, 検索範囲, 対応範囲)という形で使います。
この関数は、デフォルトでMATCH関数の検索の種類「1」と同じ動き（検索値以下の最大値を検索）をします。（近似一致）
つまり、アプローチ2でINDEXとMATCHが二人がかりでやっていた仕事を、LOOKUP関数はたった一人で、しかもよりシンプルにこなしてしまうのです。
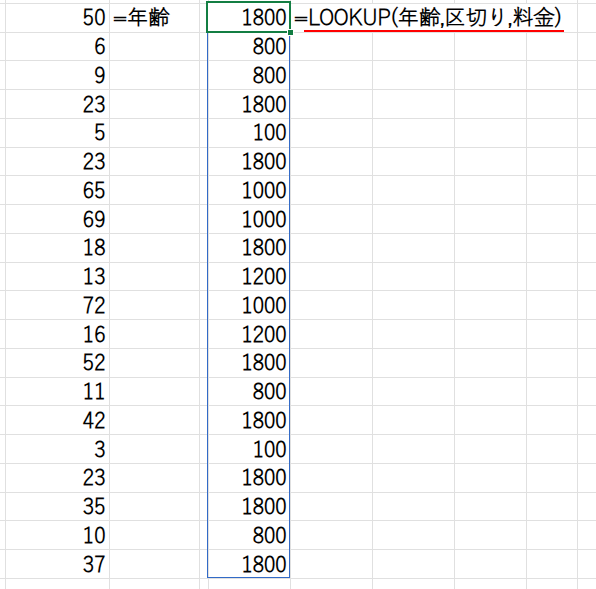
もちろん、検索範囲である「区切り」が昇順に並んでいる、という条件はありますが、今回のケースではその条件を完璧に満たしています。
時代遅れどころか、2025年の今でも、互換性も実用性も抜群の、ぜひ覚えておきたい超強力な関数です。
LOOKUP関数については以下の記事にて詳しく紹介しています！
アプローチ4：SUM + FREQUENCY（分布を調べて料金を割り当てる）
考えかた
お馴染みの関数パズル、FREQUENCY関数の登場です。
この関数は、データの分布を調べるのが得意です。
「0～5歳は何人、6～11歳は何人、12～17歳は何人…」という、各年齢層の人数をまず一気に計算します。
そして、その人数分布の配列と、料金表の配列を掛け合わせることで、総売上を算出します。
数式と解説
合計金額を表示したいセルに、以下の数式を入力します。
=SUM(FREQUENCY(年齢,{5;11;17;64})*料金)
FREQUENCY(年齢,{5;11;17;64}): この数式の核心部です。
- 第1引数: 年齢（20人分の年齢配列）
- 第2引数: {5;11;17;64} という区切り点の配列定数。
ここで重要なのは、なぜ区切り点が料金表の「区切り」{0;6;12;18;65}と違うのか、という点です。
FREQUENCY関数は、「その区切り点以下のデータ」をカウントします。つまり、
- 「5」を指定すると → 5歳以下の人数（＝幼児の人数）
- 「11」を指定すると → 6歳～11歳の人数（＝小人の人数）
- 「17」を指定すると → 12歳～17歳の人数（＝学生の人数）
- 「64」を指定すると → 18歳～64歳の人数（＝大人の人数）
- 最後に、64より大きい人数（＝シニアの人数）が自動で追加されます。
このように、料金表の区切り年齢から1を引いた値を指定する必要があるのです。この結果、{幼児の人数; 小人の人数; ...}という人数の配列が生成されます。
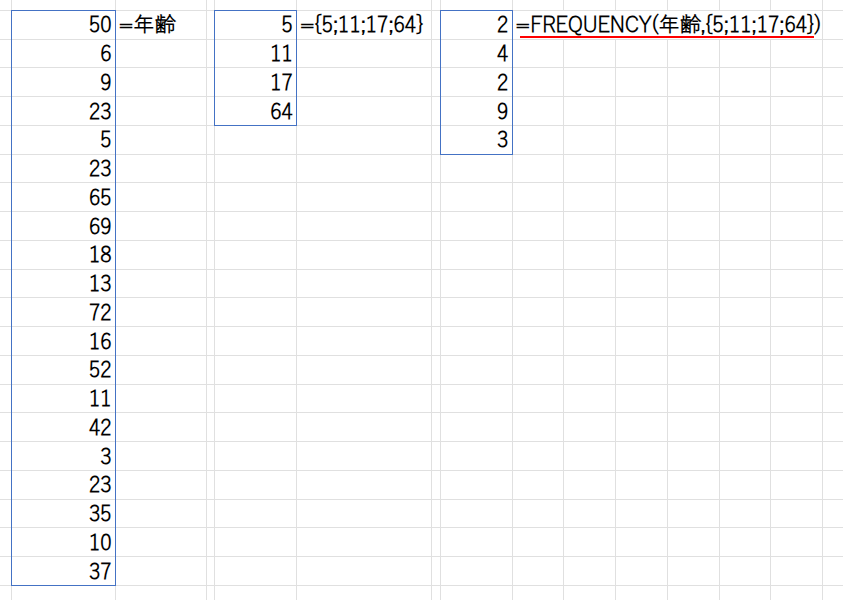
… * 料金: 生成された人数の配列と、「料金」配列（{100;800;1200;1800;1000}）を掛け合わせます。これにより、各年齢層の売上合計の配列が計算されます。
SUM(…): 最後に、各層の売上を合計して、全体の総売上を算出します。
アプローチ5：SUM + ブール演算（IFなき時代の条件分岐）
考えかた
ここからは、関数パズルの世界です。
IFS関数のような便利な関数が登場する前、複数の条件分岐は、論理値の計算（ブール演算）で行うのが一般的でした。
「年齢が●歳以上」かつ「年齢が●歳未満」という条件を、TRUE(1)/FALSE(0)の掛け算で表現し、対応する料金を掛け合わせる、という処理をすべての年齢層で行い、最後にすべてを足し合わせます。
数式と解説
合計金額を表示したいセルに、以下の数式を入力します。
=SUM((年齢<6)*100+
(年齢>=6)*(年齢<12)*800+
(年齢>=12)*(年齢<18)*1200+
(年齢>=18)*(年齢<65)*1800+
(年齢>=65)*1000)
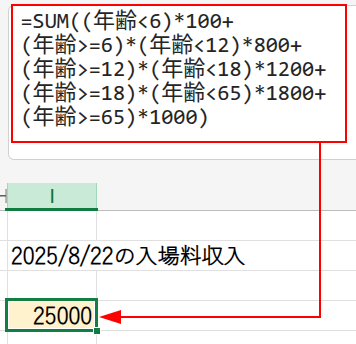
一見すると非常に長いですが、同じ構造の繰り返しです。
例えば、(年齢>=6)*(年齢<12)*800 の部分を見てみましょう。
(年齢>=6): 6歳以上の人がTRUE(1)になる配列を生成。(年齢<12): 12歳未満の人がTRUE(1)になる配列を生成。
この2つの配列を掛け合わせると、「6歳以上」かつ「12歳未満」の人だけが 1 * 1 = 1 となり、それ以外の人はすべて0になります。
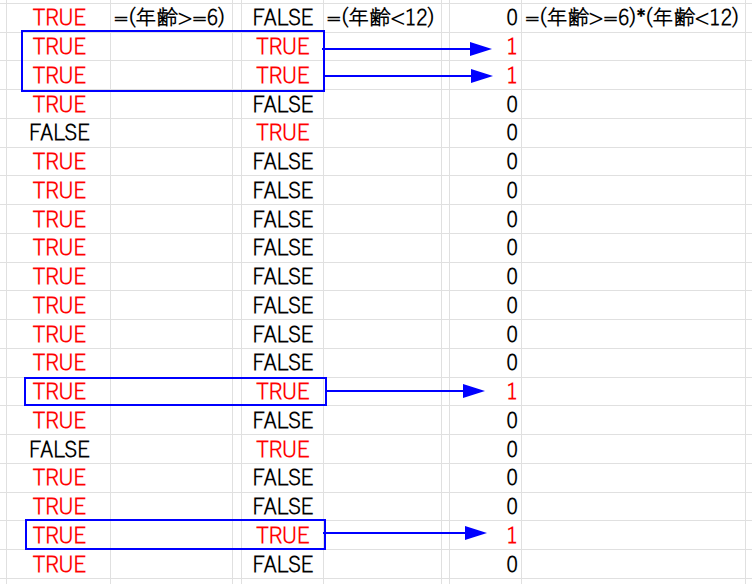
この1と0の配列に料金「800」を掛けることで、小人の料金配列が完成します。
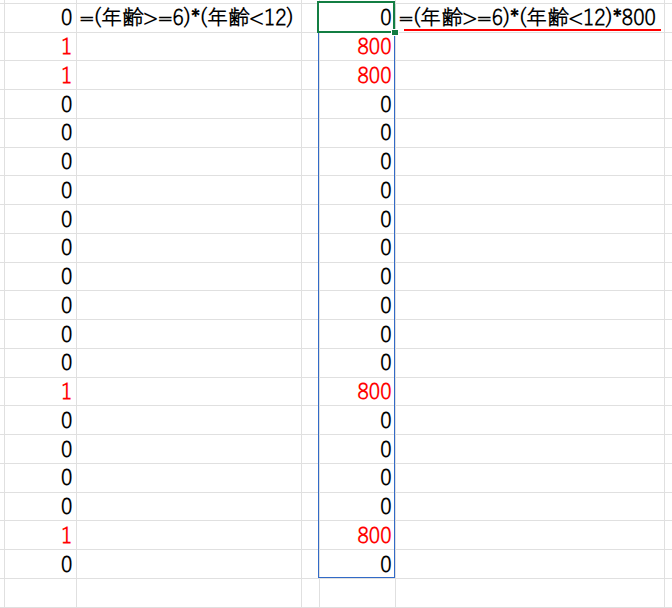
この処理をすべての料金区分で行い、最後に「+」で足し合わせています。
各個人はいずれか一つの区分にしか当てはまらないため、他の区分の計算結果は0になり、正しく個人の料金が計算された配列が出来上がります。
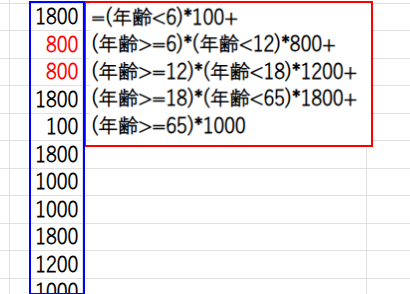
これをSUM関数で合計すれば、全体の売上が算出できます。
【補足】SUMPRODUCTかSUMか
Excel 2019以前では、このような配列計算を正しく行うにはSUMPRODUCT関数が必要でした。
しかし、現代のExcelではSUM関数自体が配列を扱えるように強化されたため、SUM関数で問題なく計算できます。
アプローチ6：SUM + 配列計算（究極の関数パズル）
考えかた
最後は、アプローチ5の考え方を、さらに配列定数を使って圧縮した数式です。
20人分の年齢が並んだ縦長の配列を、料金区分の数（5つ）だけ横にコピーした巨大な2次元配列を作り出します。
そして、その巨大な配列に対して、5つの料金区分の条件を、配列定数を使って一気にぶつけ、計算します。
数式と解説
合計金額を表示したいセルに、以下の数式を入力します。
=SUM((年齢*{1,1,1,1,1}<{6,12,18,65,200})*
(年齢*{1,1,1,1,1}>={0,6,12,18,65})*
{100,800,1200,1800,1000})
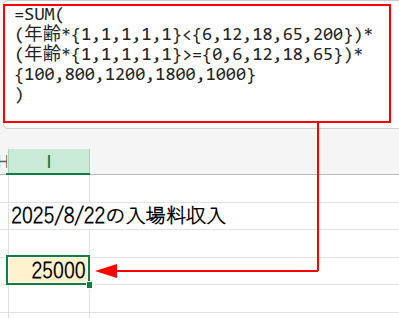
年齢*{1,1,1,1,1}: これがこの数式のキモです。
「年齢」配列（20行1列）に、横並びの配列{1,1,1,1,1}（1行5列）を掛けることで、20行5列の巨大な配列を生成します。各行には、同じ人の年齢が5つ並んでいます。
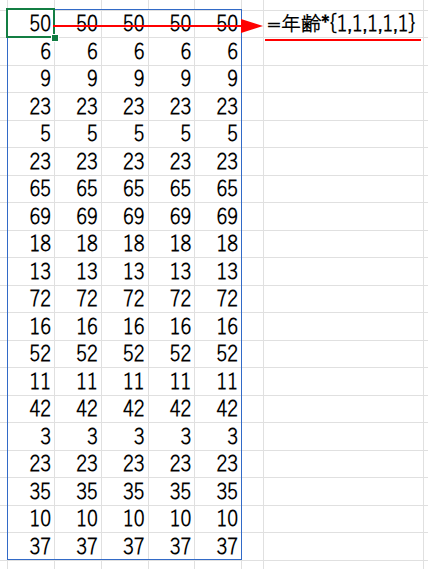
... < {6,12,18,65,200}: この巨大な配列と、「未満」の条件配列を比較します。
200は上限として適当な大きい数です。
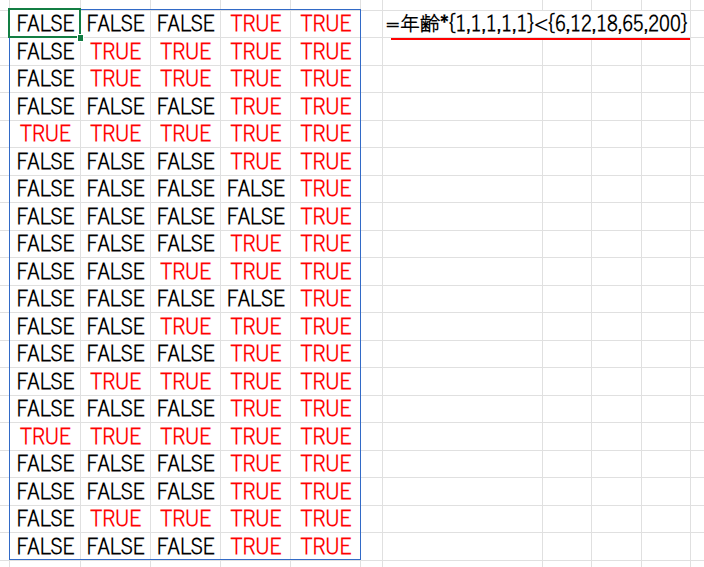
... >= {0,6,12,18,65}: 同様に、「以上」の条件配列とも比較します。
この2つの条件比較の結果（TRUE/FALSEの2次元配列）を掛け合わせることで、各行、自分が該当する料金区分の列だけが「1」になる、20行5列の配列ができます。
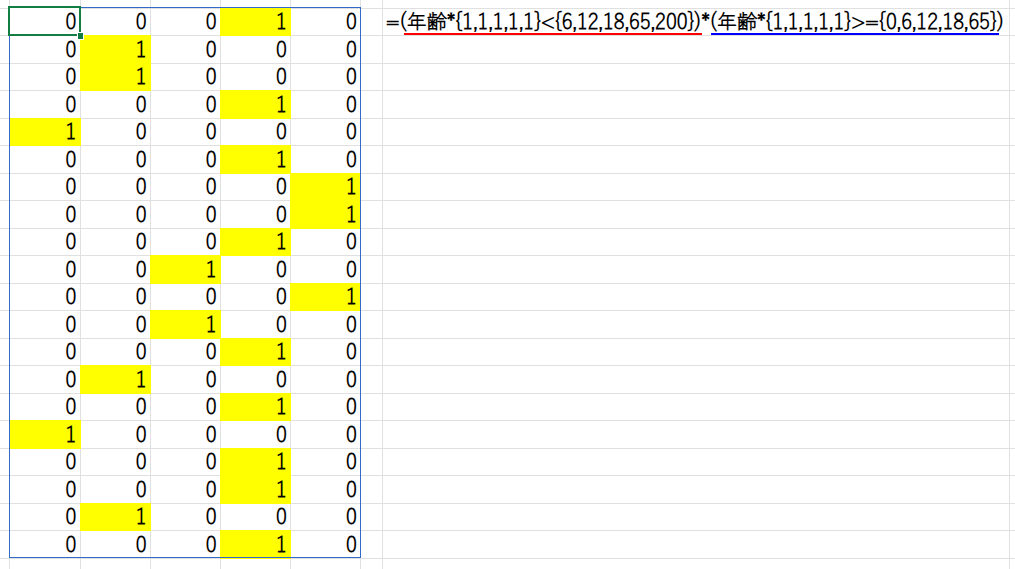
最後に、この配列に料金の配列{100,800,1200,1800,1000}を掛け合わせます。
すると、各行の「1」だった部分が、その人の正しい料金に置き換わります。
最終的に、この20行5列の配列（各行に料金が一つ、残りは0）をSUM関数で合計することで、全体の売上が計算できる、というわけです。
まとめ
今回は、「年齢別入場料の合計」という実務的なテーマを、6つの異なるアプローチで解決しました。
実務で使うなら、アプローチ1(IFS)、2(INDEX/MATCH)、そして3(LOOKUP)が断然おすすめです。
特にLOOKUP関数は、今回のケースのように条件が整っていれば、最もシンプルかつ強力な選択肢となります。
一方で、FREQUENCY関数や配列計算を使った方法は、一見すると複雑ですが、Excelが内部でどのようにデータを処理しているのかを理解する上で、非常に良い頭の体操になります。
「答えは一つ、解法は無数」
Excelの面白さは、まさにこの多様な解法の中にあります。
今回のテクニックが、皆さんの日々の業務を少しでも効率化する手助けとなれば幸いです。
