本記事では、無料のWeb版Excelを使用して検証および画像の作成を行っています。Windowsはもちろん、MacやLinuxの方もブラウザさえあれば挑戦できます！
はじめに：ABS関数を封印せよ！絶対値を求める思考の冒険
数値のマイナス符号を取り払い、0からの距離を求める「絶対値」。
Excelでは、ABS関数を使えば一瞬で計算できます。
=ABS(-100) は 100 を返す。これはExcelの基本であり、常識です。
「でも、もし…もしも、この便利なABS関数が、今日から使用禁止になったとしたら？」
あなたなら、どうやって絶対値を求めますか？
今回の記事は、そんな「もしも」の世界で繰り広げられる、思考のパズルです。
ABS関数を封印し、他の関数や計算の仕組みを駆使して「絶対値」というゴールを目指します。
数学的な正攻法から、論理的なアプローチ、文字列操作の裏ワザ、そして驚愕の関数ハックまで、多彩な解法があなたを待っています。
さあ、ABS関数への依存から脱却し、あなたのExcel脳を刺激する冒険に出かけましょう！
今回のミッション
現在の状態： A3:A9の範囲に、正の数、負の数、小数、そして0を含む、様々な数値が入力されています。
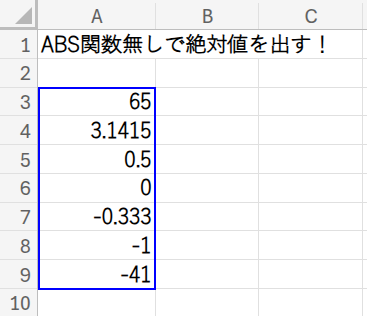
目指すゴール： これらの数値の絶対値を、ABS関数を使わずに計算します。
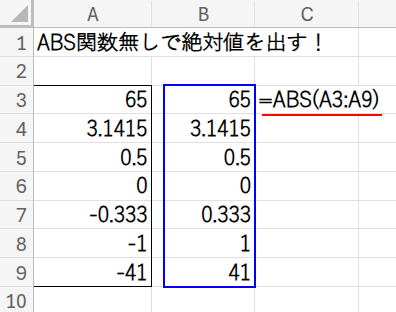
比較対象として、B列に王道である =ABS(A3:A9) の結果を表示させておきます。
これから紹介する数式が、すべてこのB列と同じ結果になることを目指します。
ABS関数を使わずに絶対値を出す9つの方法
アプローチ1：SQRT + 2乗（数学の正攻法）
考えかた
まずは、数学の教科書にも載っている、最も正統なアプローチです。
絶対値の定義は「0からの距離」ですが、数学的には「ある数を2乗して、その平方根を取ったもの」とも言えます。
どんな数値も、2乗すれば必ず正の数（または0）になります。
その性質を利用した、非常にエレガントな方法です。
数式と解説
C3セルに、以下の数式を入力します。
=SQRT(A3:A9^2)
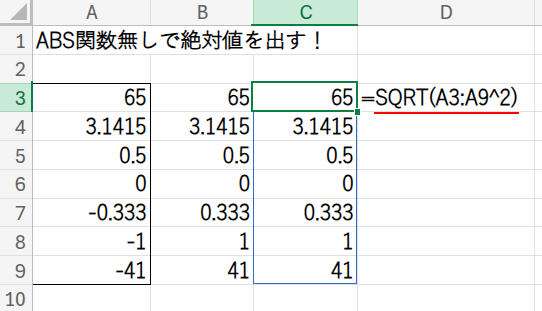
・A3:A9^2: まず、A3:A9の範囲にある数値をすべて「2乗」します。
これにより、-0.333は0.110889に、-41は1681に変換され、すべての数値が正になります。
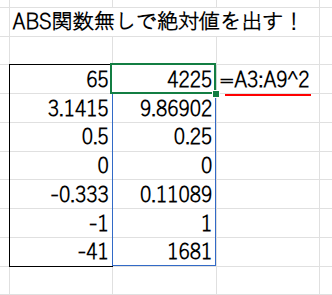
・SQRT(...): 次に、SQRT関数（平方根を求める関数）が、2乗された数値のルートを計算します。
1681の平方根は41なので、見事に元の数値の絶対値が求められる、というわけです。
アプローチ2：SIGN関数（符号を味方につける）
考えかた
次に紹介するのは、数値の「符号」そのものを利用する方法です。
SIGN関数は、数値の符号を判定し、正なら「1」、負なら「-1」、ゼロなら「0」を返す、まるで審判のような関数です。
この性質を利用すれば、「負の数にだけ-1を掛けて、正の数に変える」という処理が実現できます。
数式と解説
C3セルに、以下の数式を入力します。
=SIGN(A3:A9)*A3:A9
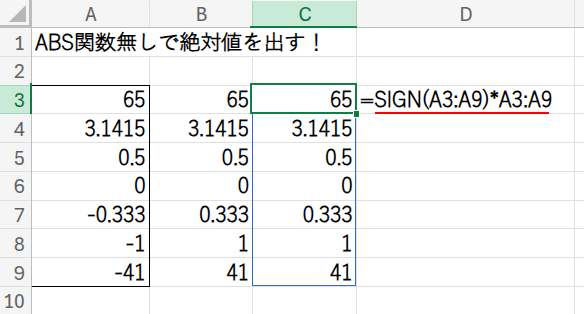
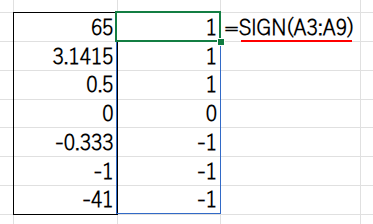
・SIGN(A3:A9): まず、SIGN関数がA3:A9の各数値の符号を判定し、{1;1;1;0;-1;-1;-1} という符号の配列を生成します。
・... * A3:A9: この符号の配列と、元の数値の配列を掛け合わせます。
・正の数（例: 65）の場合 → 1 * 65 = 65
・負の数（例: -41）の場合 → -1 * -41 = 41
・ゼロの場合 → 0 * 0 = 0
このように、元の数値にその数値自身の符号を掛け合わせることで、すべての数値が正（または0）になる、という巧妙なロジックです。
アプローチ3：IF関数（論理で攻める基本形）
考えかた
最もプログラミング的な発想に近い、論理的なアプローチです。
絶対値のルールを、そのままIF関数で表現します。
「もし、数値が0より小さかったら（マイナスだったら）、-1を掛けてプラスにする。そうでなければ、そのままの数値を使いなさい」
という、非常に分かりやすい条件分岐です。
数式と解説
C3セルに、以下の数式を入力します。
=IF(A3:A9<0,-A3:A9,A3:A9)
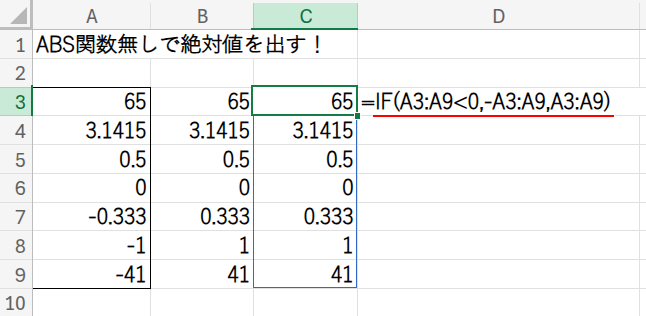
・A3:A9<0: まず、A3:A9の各数値が0より小さいかどうかを判定します。
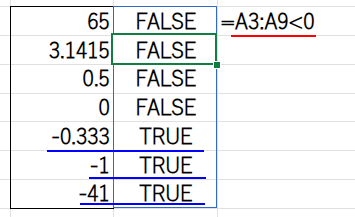
・-A3:A9: 条件が真（TRUE）の場合の処理です。元の数値にマイナスを付ける（-1を掛ける）ことで、負の数を正の数に変換します。
・A3:A9: 条件が偽（FALSE）の場合の処理です。元の数値（正の数または0）をそのまま返します。
Excelが配列の各要素に対してこのIF判定を一括で行い、結果をスピルさせてくれます。
アプローチ4：ブール演算（IF関数からの卒業）
考えかた
やっていることはアプローチ3と全く同じですが、IF関数を使わずに、論理値の計算（ブール演算）だけで実現する方法です。
Excelでは、計算式の中で論理値のTRUEは「1」、FALSEは「0」として扱われます。
この性質を利用して、「負の数のグループ」と「正の数のグループ」を別々に計算し、最後に足し合わせます。
数式と解説
C3セルに、以下の数式を入力します。
=(A3:A9<0)*-A3:A9+(A3:A9>0)*A3:A9
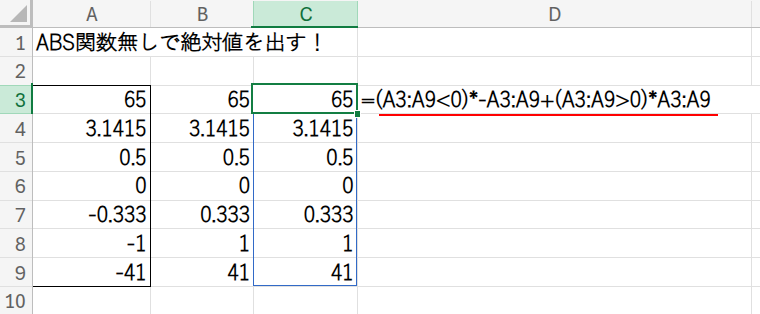
この数式は、2つのパートの足し算で構成されています。
・(A3:A9<0)*-A3:A9: 最初のパートです。(A3:A9<0)が、負の数だけがTRUE(1)になる配列を生成します。
これに-A3:A9（元の数値をプラスに変換したもの）を掛けることで、負の数だけが絶対値に変換され、他はすべて0になります。
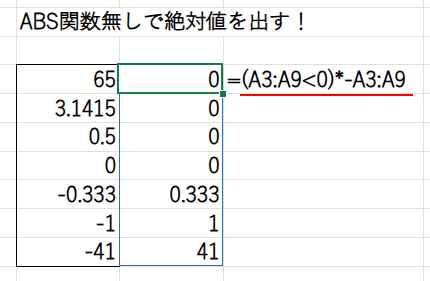
・(A3:A9>0)*A3:A9: 2番目のパートです。
同様に、正の数だけがTRUE(1)になる配列に、元の数値を掛け合わせます。
これにより、正の数だけがそのまま残り、他はすべて0になります。
最後に、この2つの配列を足し合わせます。
各数値はどちらか一方の配列にしか値がない（もう一方は0）ため、見事に絶対値の配列が完成します。（0の場合は 0*0 + 0*0 で0になります）
アプローチ5：SUBSTITUTE（文字列操作の裏ワザ）
考えかた
ここで全く異なる視点が登場します。
「絶対値とは、要するにマイナス記号『-』を取り除いたものではないか？」という、数値を一度「文字列」として捉えるアプローチです。
SUBSTITUTE関数を使って、力技でマイナス記号を消し去ります。
数式と解説
C3セルに、以下の数式を入力します。
=VALUE(SUBSTITUTE(A3:A9,”-“,””))
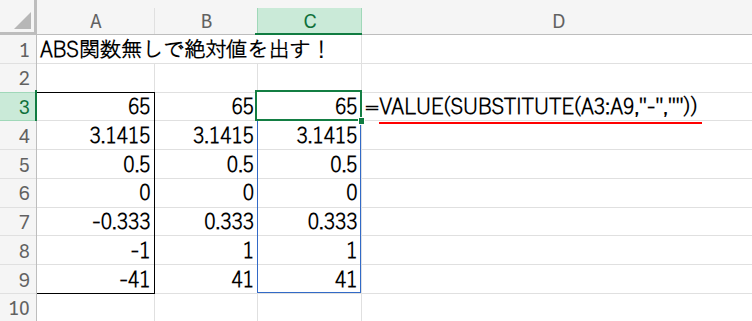
・SUBSTITUTE(A3:A9,"-",""): まず、SUBSTITUTE関数（文字列を置換する関数）が、A3:A9の範囲を文字列とみなし、その中にある「-」という文字を、すべて「””」（空白）に置き換えます。
これにより、「-41」は「41」という”文字列“になります。
・VALUE(...): SUBSTITUTE関数の結果はあくまで文字列なので、このままでは計算に使えません。
そこで、VALUE関数を使って、数字の文字列を本物の「数値」に変換して、ゴールとなります。
アプローチ6：MAX + 配列定数（スピルしない単セル版）
考えかた
配列定数を使った、面白い発想の転換です。
「ある数値（例: -41）」と、「それに-1を掛けた数値（例: 41）」の2つを比べれば、大きい方が必ず絶対値になる、という考え方です。
この比較をMAX関数で行います。
数式と解説
C3セルに、以下の数式を入力します。（※これはスピルしません）
そして、C9セルまでフィルコピーします。
=MAX(A3*{1,-1})
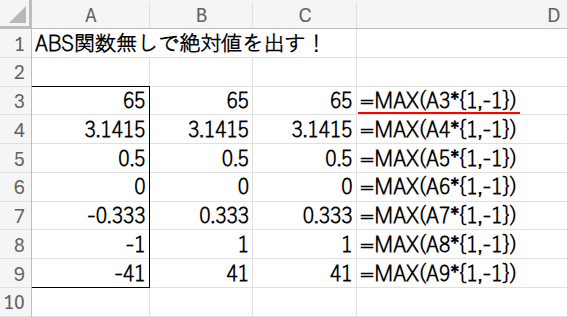
・A3*{1,-1}: A3セルの値に、配列定数{1,-1}を掛け合わせます。
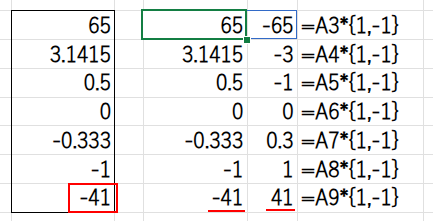
もしA9が「-41」なら、{-41*1,-41*-1} という計算が行われ、{-41,41} という2つの要素を持つ配列がメモリ上に生成されます。
・MAX(...): MAX関数が、この{-41,41}の中から最大値である「41」を選び出します。
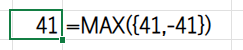
この方法は非常にクレバーですが、このままでは配列を扱えず、単一のセルにしか機能しません。これをスピルさせるには、次のアプローチが必要です。
アプローチ7：MAP + LAMBDA（最新関数でスピルを実現）
考えかた
アプローチ6のロジックを、範囲全体に適用してスピルさせるための現代的な解決策が、MAP関数とLAMBDA関数の組み合わせです。
MAP関数は、指定した配列の各要素を一つずつ取り出し、LAMBDA関数で定義した「自作の処理」を適用して、新しい配列を生成する、という高度な機能を持っています。
数式と解説
C3セルに、以下の数式を入力します。
=MAP(A3:A9, LAMBDA(x, MAX(x*{1,-1})))
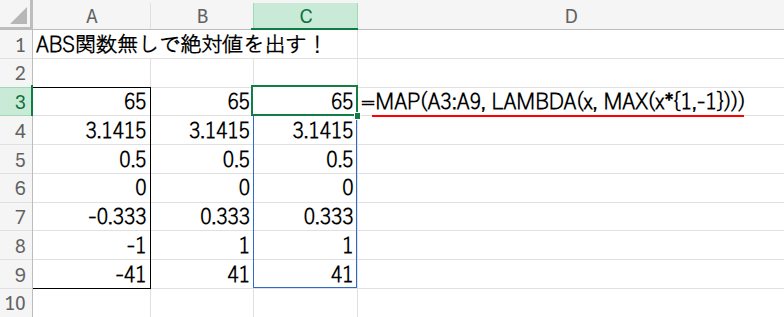
・MAP(A3:A9, ...): MAP関数が、A3:A9の配列を一つずつ（A3, A4, A5…と）処理していくことを宣言します。
・LAMBDA(x, ...): 各要素に対して行う処理のレシピをLAMBDA関数で定義します。引数xには、MAP関数が取り出した各要素（A3の値、A4の値…）が順番に格納されます。
・MAX(x*{1,-1}): これが処理の本体です。アプローチ6と全く同じロジックで、引数xの絶対値を計算します。
MAP関数が、A3からA9までのすべての数値に対してこのLAMBDA処理を繰り返し、得られたすべての結果をまとめて一つの配列としてスピルさせてくれるのです。
アプローチ8：LOOKUP（知る人ぞ知る名関数の応用）
考えかた
再び登場、古くて新しい名関数LOOKUPです。
LOOKUP関数については以下の記事でも紹介しています。
アプローチ2のSIGN関数と考え方は似ていますが、これをLOOKUP関数で代用します。
「負の数なら-1、0以上なら1」を返す仕組みをLOOKUPで作り出し、元の数値に掛け合わせます。
数式と解説
C3セルに、以下の数式を入力します。
=LOOKUP(A3:A9,MIN(A3:A9)*{1,0},{-1,1})*A3:A9
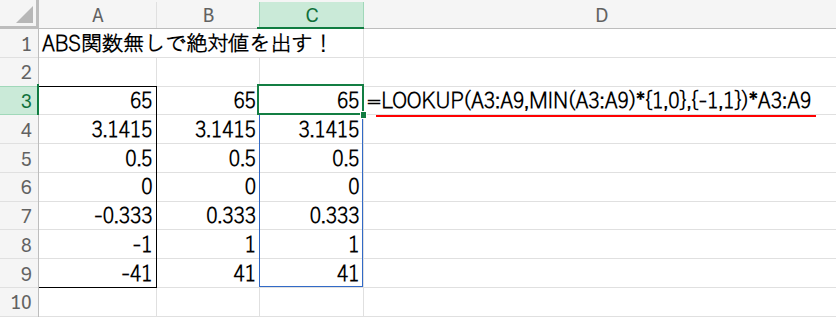
・MIN(A3:A9)*{1,0}: まず、検索範囲を作ります。範囲内の最小値（-41）を使い、{-41, 0}という配列を生成します。
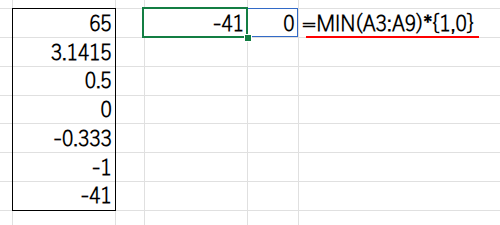
・LOOKUP(A3:A9,{-41,0},{-1,1}): LOOKUP関数が、A3:A9の各数値を、この{-41,0}という検索範囲で探します。
・負の数の場合、検索値以下の最大値は「-41」なので、対応する結果「-1」が返ります。
・0または正の数の場合、検索値以下の最大値は「0」なので、対応する結果「1」が返ります。
・... * A3:A9: この結果得られた「-1」と「1」の配列を、元の数値配列に掛け合わせることで、絶対値が計算されます。
アプローチ9：三角関数（超絶技巧の関数ハック）
考えかた
最後は、実用性は皆無、完全に「関数パズル」として楽しむための、三角関数を使った驚愕のハックです。
COS関数とACOS関数（逆余弦）の数学的な性質を利用して、絶対値と同じ結果を導き出します。
【超重要】
この方法は、数学的な性質上、絶対値が1未満の小数（例: 0.5, -0.333）では正しい結果を返しません。あくまで「こんなこともできる」という余興としてお楽しみください。
数式と解説
C3セルに、以下の数式を入力します。(誤差をわかりやすくするために表の数値を変えています。)
=IFERROR(1/ACOS(COS(1/A3:A9)),0)
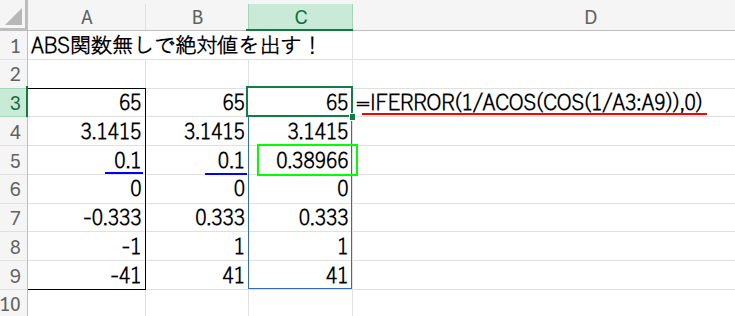
この数式は、三角関数の複雑な関係性に基づいています。
ACOS(COS(x))という組み合わせは、xの値を、ACOS関数の定義域である正の値の範囲に変換する働きがあります。
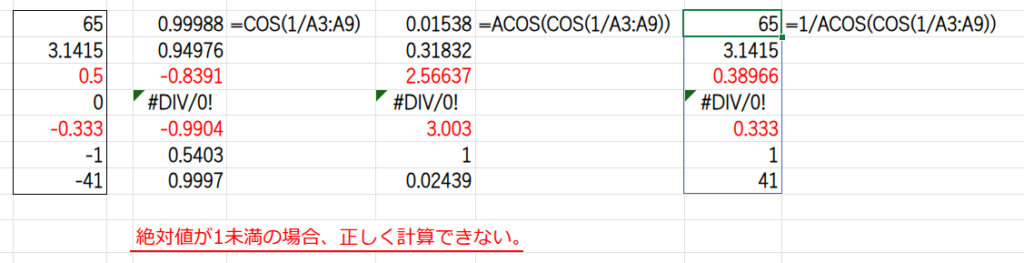
この性質を、数値の逆数（1/x）に対して適用し、最後に再び逆数に戻すことで、元の数値の絶対値に似た値を計算しています。
0で割るエラーを回避するためにIFERROR関数で0を返す処理も加えています。
前述の通り、この方法は万能ではありませんが、Excel関数の組み合わせの意外性を示す、非常に面白い例と言えるでしょう。
まとめ
今回は、「ABS関数を使わずに絶対値を求める」というテーマで、9つもの異なるアプローチを探求しました。
もちろん、実務で絶対値を求めたいときは、迷わずABS関数を使ってください。
それが最も速く、正確で、誰にでも分かりやすい最善の方法です。
しかし、今回紹介したような代替案を考えてみることは、
- 数学的なアプローチ（2乗とルート）
- 論理的なアプローチ（IF、ブール演算）
- データ型を変換するアプローチ（文字列操作）
- 配列を駆使するアプローチ（MAX、MAP）
など、Excelが持つ多様な計算能力と、一つのゴールに対して無数の解法が存在するという、関数の世界の面白さを教えてくれます。
今回の関数パズルが、皆さんのExcelへの知的好奇心を刺激するきっかけになれば幸いです。
