本記事では、無料のWeb版Excelを使用して検証および画像の作成を行っています。Windowsはもちろん、MacやLinuxの方もブラウザさえあれば挑戦できます！
はじめに：LEN関数、本日より使用禁止！
Excelで文字数を数えるとき、私たちが真っ先に思い浮かべるのは、もちろんLEN関数です。
そのシンプルさと確実さから、「文字数カウントの王様」と言っても過言ではないでしょう。
「では、もし…もしも、この絶対的な王様であるLEN関数が、今日から使用禁止になったとしたら？」
あなたなら、どうやって文字数を数えますか？
今回の記事は、そんな「もしも」の世界で繰り広げられる、思考のパズルです。
LEN関数を封印し、他の関数やExcelの計算の仕組みを駆使して「文字数を数える」というゴールを目指します。
一見、奇想天外に見える数式たち。しかし、その一つひとつを分解していくと、Excelの奥深いロジックが見えてくるはずです。
さあ、LEN関数の呪縛から解き放たれ、あなたのExcel脳をフル回転させる冒険に出かけましょう！
今回のミッション
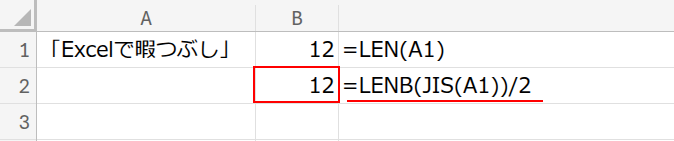
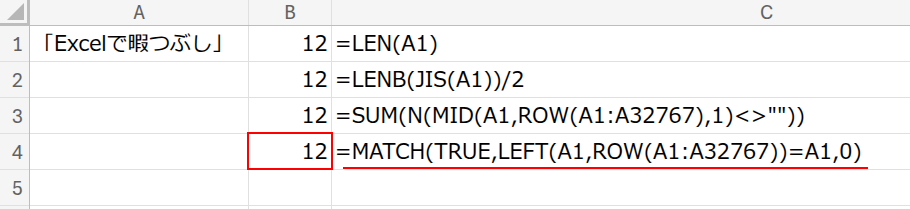
現在の状態： A1セルに、今回の”お題”となる文字列”「Excelで暇つぶし」“が入力されています。
目指すゴール： この文字列の文字数（答えは「12」）を、LEN関数を使わずに計算します。
比較対象として、B1セルに王道である =LEN(A1) の結果を表示させておきます。
これから紹介する数式が、すべてこのB1セルと同じ「12」という結果になることを目指します。
LEN関数を使わずに文字数を数える5つの方法
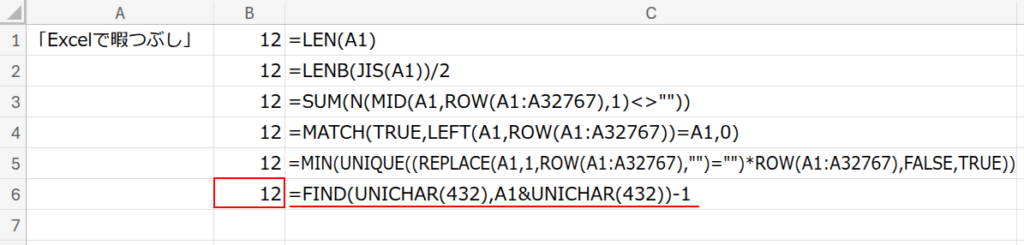
アプローチ1：LENB + JIS（バイト数からの逆算）
考えかた
「LEN関数は禁止」と言いましたが、その兄弟分であるLENB関数が禁止とは言っていません（笑）。
しかし、LENB関数は文字数ではなく「バイト数」を数えるため、半角英数字は「1」、全角ひらがなは「2」としてカウントされ、単位がバラバラです。
そこで、JIS関数という普段あまり使わない助っ人を呼びます。
JIS関数は、すべての文字を「全角（2バイト）」に強制的に変換する力を持っています。
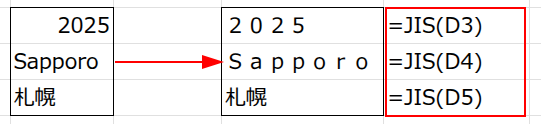
つまり、「すべての文字を全角に揃えてからバイト数を数え、最後に2で割れば、文字数になるのでは？」という作戦です。
数式と解説
B2セルに、以下の数式を入力します。
=LENB(JIS(A1))/2
この数式は、内側から順に処理されます。
・JIS(A1): まず、JIS関数がA1セルの文字列を処理します。
半角の「Excel」が、全角の「Ｅｘｃｅｌ」に変換されます。
これにより、文字列内のすべての文字が「全角（2バイト）」として扱われるようになります。
・LENB(...): 次に、LENB関数が、すべて全角に変換された文字列の「バイト数」を数えます。
12文字すべてが2バイトなので、12 * 2 = 24 という結果が返ってきます。
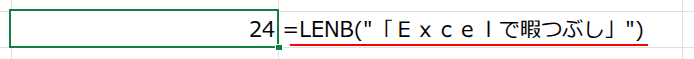
・... / 2: 最後に、計算された合計バイト数「24」を2で割ることで、目的の文字数「12」を導き出します。
【ご注意】
この方法は、Excelの文字コードの扱い方（エンコーディング）に依存するため、環境によっては意図しない結果になる可能性もゼロではありません。今回はWeb版Excelで動作することを確認しています。
アプローチ2：SUM + N + MID + ROW（1文字ずつの存在確認）
考えかた
次に紹介するのは、文字列を1文字ずつに分解し、「そこに文字が存在するか？」を判定して合計するという、非常に地道で、しかし確実なアプローチです。
まるで、文字列の先頭から一歩一歩進んでいき、足跡の数を数えるようなイメージです。
数式と解説
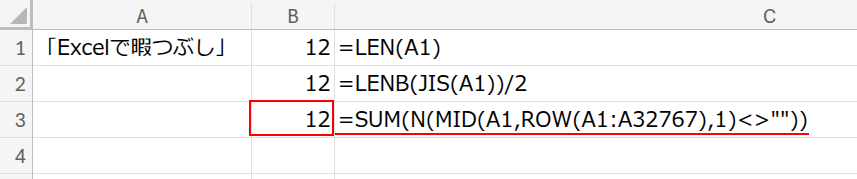
B3セルに、以下の数式を入力します。
=SUM(N(MID(A1,ROW(A1:A32767),1)<>””))
この長い数式も、内側から分解していきましょう。
・ROW(A1:A32767): まず、ROW関数を使って、{1;2;3;...;32767} という、とてつもなく巨大な連番の配列をメモリ上に生成します。
なぜ「32767」かというと、これがExcelの1つのセルに入力できる最大文字数だからです。これで、どんなに長い文字列が来ても対応できます。
・MID(A1, ..., 1): 次に、MID関数（文字列の中から指定した位置の文字を抜き出す関数）が、この巨大な連番を使って、A1セルの文字列を「1文字目から1文字」「2文字目から1文字」…と、1文字ずつ抜き出していきます。
結果として、{"「";"E";"x";...;"」";"";"";...} という、12個の文字と大量の空白（””）が並んだ配列ができます。
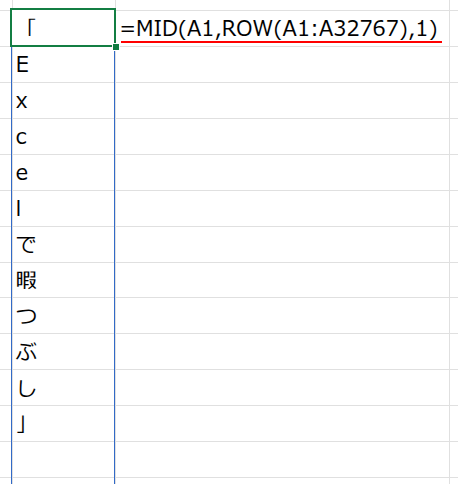
・... <>"": この配列の各要素が、空白（””）ではないかを判定します。文字がある部分はTRUE、空白の部分はFALSEとなり、{TRUE;TRUE;...;TRUE;FALSE;FALSE;...} という論理値の配列に変換されます。
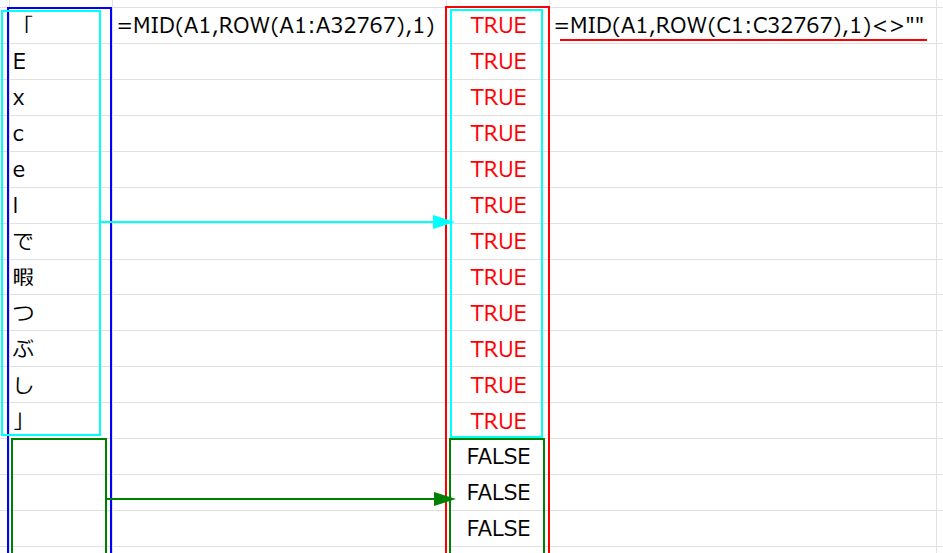
・N(...): N関数が、この論理値の配列を数値に変換します。TRUEは「1」に、FALSEは「0」になります。結果は {1;1;...;1;0;0;...} という、1が12個並んだ数値の配列です。
・SUM(...): 最後に、SUM関数がこの配列を合計します。1が12個あるので、合計は「12」となり、見事に文字数を数え上げました。
アプローチ3：MATCH + LEFT + ROW（文字列が完成する瞬間を探す）
考えかた
これは、非常に巧妙なロジックパズルです。
文字列の左側から1文字、2文字、3文字…と順番に抜き出していき、「抜き出した部分文字列」が「元の文字列全体」と完全に一致する瞬間を探します。
その「瞬間」が何文字目であったかが、そのまま文字数になる、という考え方です。
数式と解説
E1セルに、以下の数式を入力します。
=MATCH(TRUE,LEFT(A1,ROW(A1:A32767))=A1,0)
・LEFT(A1,ROW(A1:A32767)): LEFT関数（文字列の左から指定した文字数を抜き出す関数）と、先ほども使った巨大な連番配列を組み合わせます。
これにより、{"「";"「E";"「Ex";...;"「Excelで暇つぶし」";...} という、だんだん長くなる文字列の配列が生成されます。
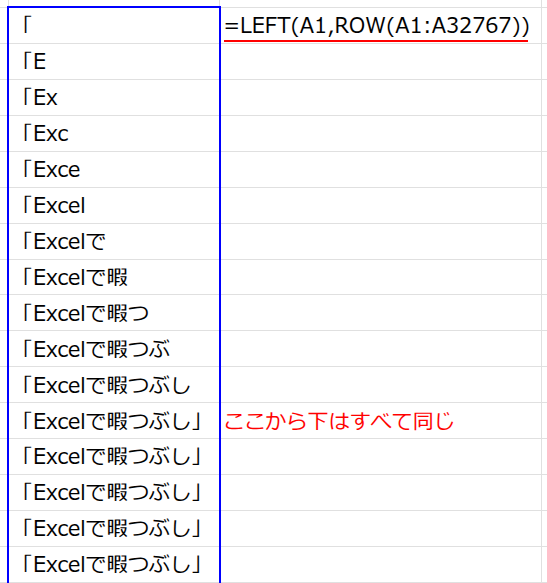
・... = A1: この配列の各要素が、元の文字列A1と等しいかどうかを判定します。
11文字目まではFALSEですが、12文字目で初めて完全に一致し、TRUEになります。
結果は、{FALSE;FALSE;...;FALSE;TRUE;TRUE;...} という論理値の配列です。（12文字目以降も、LEFT関数は最大文字数までしか返さないためTRUEが続きます）
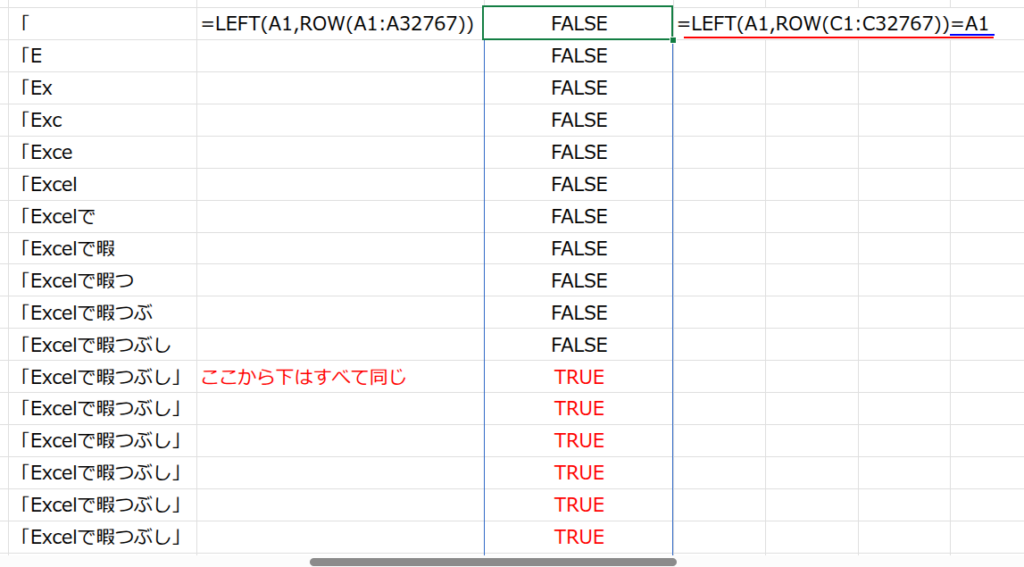
・MATCH(TRUE, ..., 0): 最後に、MATCH関数（配列の中から指定した値が最初に現れる位置を返す関数）の出番です。
この関数が、先ほどの論理値の配列の中から、TRUEが「最初に」現れる位置を探します。
最初に現れるのは12番目なので、結果として「12」が返ってくるのです。
【ご注意】
この方法は、A1セルが数値の場合はエラーに、空白の場合は「1」を返してしまうという弱点があります。今回は文字列が対象なので問題ありません。
アプローチ4：MIN + UNIQUE + REPLACE + ROW（超絶技巧の分解パズル）
考えかた
これは、実用性は皆無、完全に「関数パズル」として楽しむための超絶技巧です。
発想はアプローチ2に似ていますが、文字列を「削っていく」という逆の視点を使います。
文字列の先頭から1文字、2文字、…と順番に削除していき、文字列が「完全に空っぽ（””）になる」のは何文字削除したときかを突き止めます。
数式と解説
B5セルに、以下の数式を入力します。
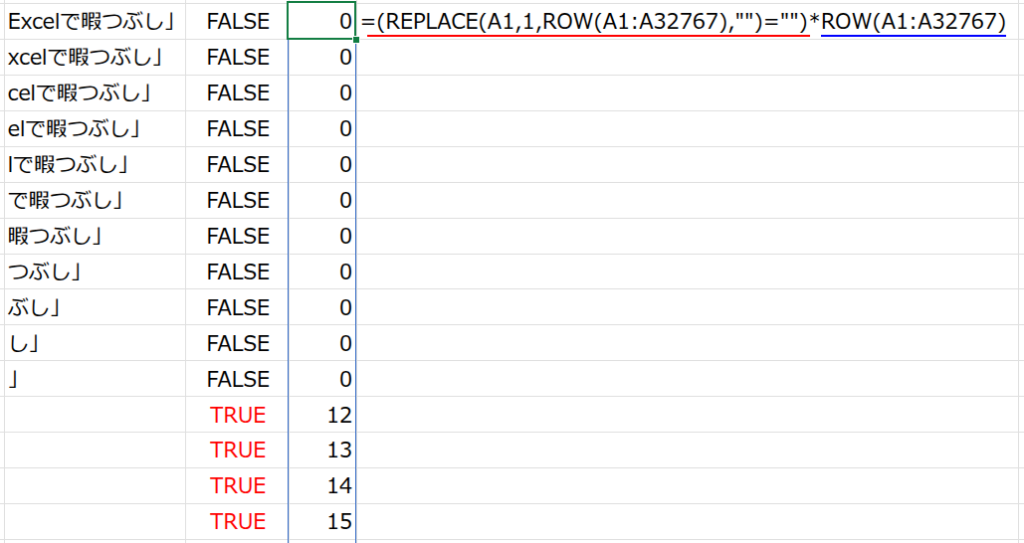
=MIN(UNIQUE((REPLACE(A1,1,ROW(A1:A32767),””)=””)*ROW(A1:A32767),FALSE,TRUE))
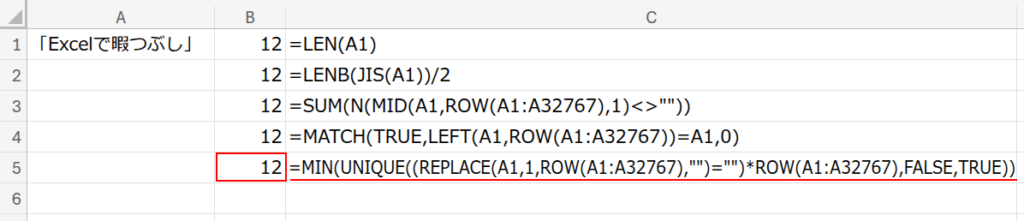
この数式は、まるで精密機械のように各関数が連携します。
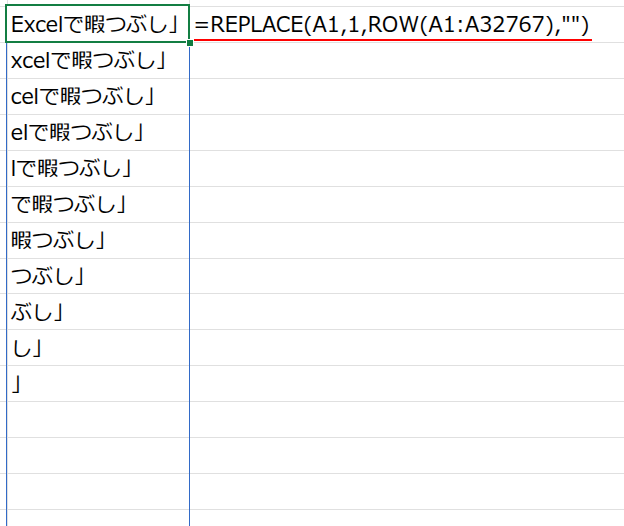
・REPLACE(A1,1,ROW(A1:A32767),""): REPLACE関数（文字列の一部を置換する関数）を使い、A1セルの1文字目から、連番配列の数だけ文字を削除（””に置換）していきます。
これにより、{"「Excelで暇つぶし」";"Excelで暇つぶし」";...} のように、だんだん短くなる文字列の配列ができます。
・... = "": この配列が、いつ空白（””）になるかを判定します。12文字を削除した瞬間に初めてTRUEになりますね。結果は {FALSE;...;TRUE;TRUE;...} という論理値の配列です。
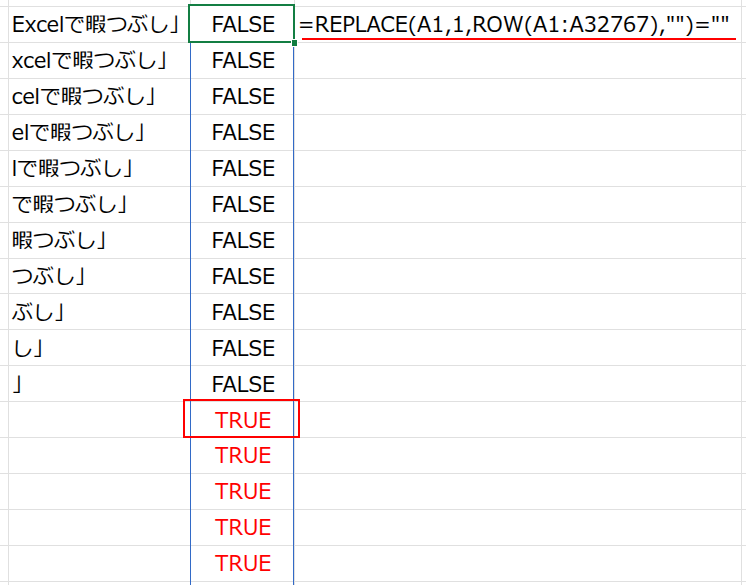
・... * ROW(A1:A32767): この論理値の配列に、連番の配列を掛け合わせます。
FALSEの部分は0になり、TRUEの部分だけが自身の行番号（12, 13, 14…）になります。
結果は {0;0;...;0;12;13;...} という数値の配列です。
・UNIQUE(...,FALSE,TRUE): ここが巧妙なトリックです。UNIQUE関数に特殊な引数を渡すことで、この配列から「重複する値」を取り除き、{12;13;14;...} という純粋な連番の配列を抽出します。
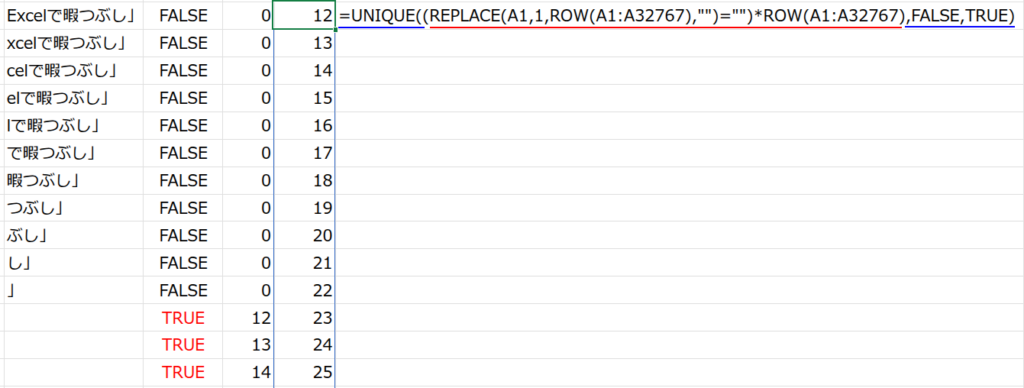
・MIN(...): 最後に、この配列の中で最も小さい値、つまり「12」をMIN関数で取り出してゴールです。
まるで宇宙船でコンビニに行くような壮大な数式ですが、そのロジックは美しいですね。
【ご注意】
この方法は、文字列が3文字以上の場合にのみ正しく機能する、という制約があります。
アプローチ5：FIND + UNICHAR（絶対に存在しない文字を探す）
考えかた
最後は、テキスト操作の古典的ながら非常に賢いテクニックです。
「もし、文字列の最後に、絶対にその文字列の中には存在しない『特別な目印』を付けられたら、その目印の位置を探すことで全体の長さが分かるのではないか？」という発想です。
数式と解説
B6セルに、以下の数式を入力します。
=FIND(UNICHAR(432),A1&UNICHAR(432))-1
・UNICHAR(432): まず、UNICHAR関数（指定した番号の文字を返す関数）を使って、「特別な目印」を生成します。
UNICHAR(432)は「ư」という文字を返します。
これはベトナム語などで使われる文字で、通常の日本語の文章に含まれる可能性は限りなくゼロに近いです。
・A1 & UNICHAR(432): &（アンパサンド）を使って、元の文字列の末尾に、この目印「ư」を連結します。
メモリ上には「”「Excelで暇つぶし」ư”」という新しい文字列が作られます。
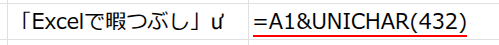
・FIND(..., ... ): FIND関数（文字列の中で、特定の文字が何番目にあるかを探す関数）が、この新しい文字列の中から目印「ư」を探します。
目印は一番最後に付けたので、その位置は「13」番目になります。
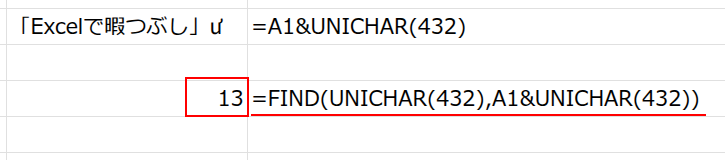
・... - 1: 最後に、見つかった位置「13」から1を引くことで、元の文字列の長さである「12」が求められます。
まとめ
今回は、「LEN関数を使わずに文字数を数える」というテーマで、5つの異なるアプローチを探求しました。
もちろん、実務で文字数を数えたいときは、迷わずLEN関数を使ってください。
それが最も速く、正確で、誰にでも分かりやすい最善の方法です。
しかし、今回の関数パズルは、普段当たり前に使っている「文字数を数える」という単純な作業が、Excelの内部では
- バイトという単位で捉えること
- 1文字ずつに分解して存在を確かめること
- 文字列が完成する瞬間を探すこと
- 絶対に存在しない目印を付けること
など、いかに多様なロジックで実現できるかを示してくれました。
こうした代替案を考えてみることは、Excel関数の組み合わせや、その本質的な動作を理解するための、最高の思考トレーニングになります。
今回の「暇つぶし」が、皆さんのExcelへの知的好奇心を刺激するきっかけになれば幸いです。
