本記事では、無料のWeb版Excelを使用して検証および画像の作成を行っています。Windowsはもちろん、MacやLinuxの方もブラウザさえあれば挑戦できます！
はじめに：Excelの果て「XFD列」への挑戦状
皆さんは、Excelのシートを右へ右へとスクロールし続けたことがありますか？
「Z列」の次が「AA列」になるのはご存知の方も多いでしょう。
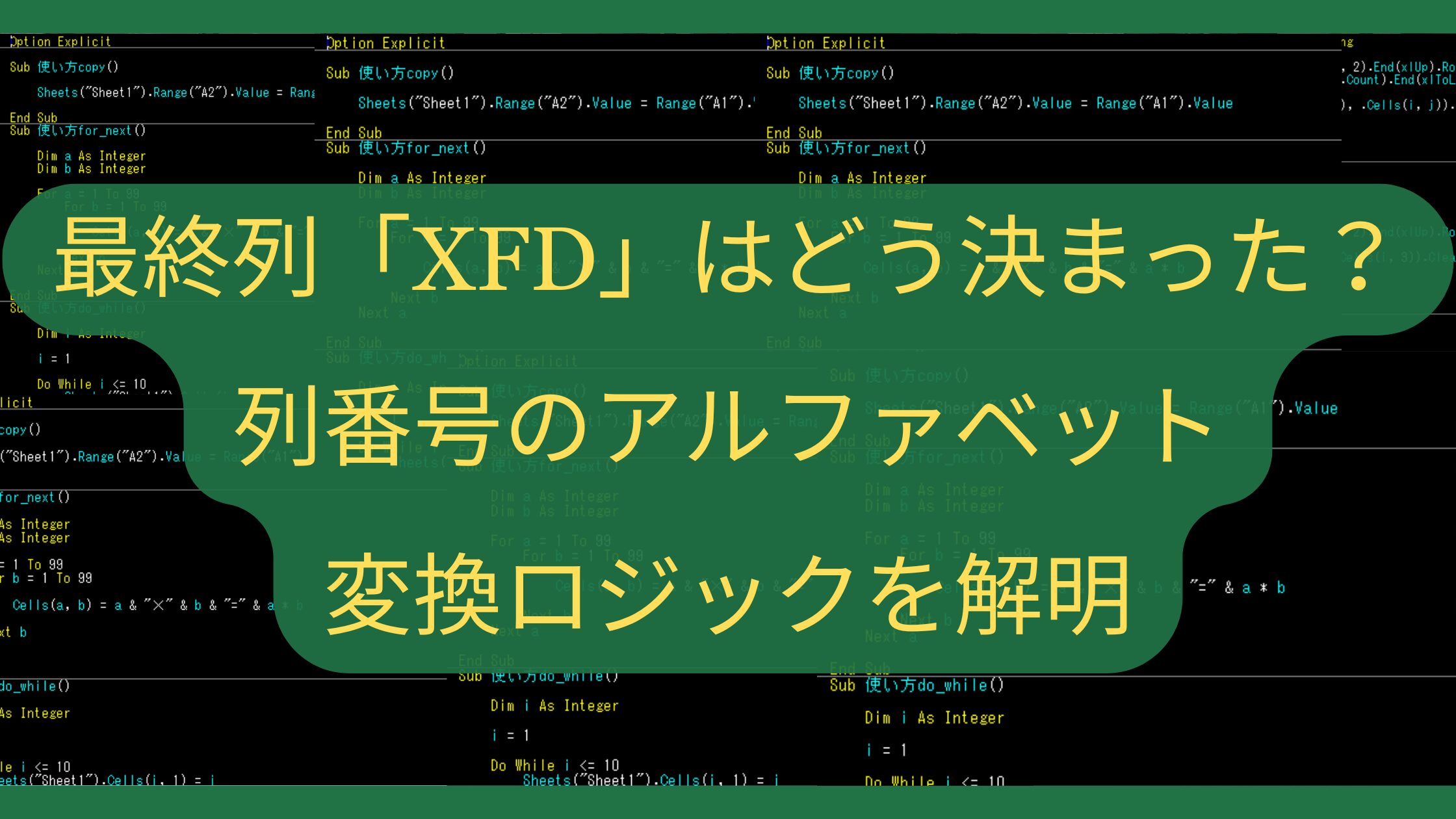
では、その遥か先、Excelシートの本当の果てが何という名前の列なのか、ご存知でしょうか？
答えは「XFD列」。実に、16384番目の列です。壮大ですよね。
「A, B, …, Z, AA, AB, …」この規則性、一体どうなっているんだろう？
もし、列番号からこの文字列を生成するADDRESS関数がなかったら、どうやって計算すればいいんだろう？
今回の記事は、そんなExcelの根幹に関わる謎に、関数だけで挑む思考のパズルです。
普段、私たちが当たり前に目にしている「列のアルファベット」が、どのようなロジックで生成されているのかを、作業列を使いながら一つひとつ分解し、自らの手で16384列すべてを再現していきます。
さあ、Excelの設計思想に触れる、知的な冒険の始まりです！
今回のミッションと準備
目指すゴール： Excelの1列目「A」から16384列目「XFD」までのすべての列文字を、ADDRESS関数を使わずに、数式だけで生成する。
アプローチ： 複雑な数式を一行で書くのではなく、1桁目、2桁目、3桁目と、パーツを別々の行（作業列ならぬ作業行ですね！）に作り、最後にそれらを結合するという、分かりやすさを重視した方法で進めます。
準備1：広大なフィールドを見渡す「ウィンドウ枠の固定」
今回は16384列という広大な範囲を扱います。
作業の途中で最終列「XFD」の結果を確認しやすいように、最初に「ウィンドウ枠の固定」を設定しておきましょう。
以下、WEB版Excelの手順です。
例えば、K列を選択した状態で、「表示」タブから「ウィンドウ枠の固定」→「選択時に固定する」をクリックすると、A〜J列を常に表示したまま、右にスクロールできるようになります。
準備2：正解（ADDRESS関数）を用意する
私たちのロジックが正しいかどうかを最後に判定するために、まず「正解」となる列文字を1行目に表示させておきましょう。
A1セルに、以下の数式を入力し、シートの右端（XFD列）までフィルコピー（または、行全体にコピー）してください。
=SUBSTITUTE(ADDRESS(1,COLUMN(),4,1),"1","")
この数式は、
COLUMN()で現在の列番号を取得し、ADDRESS(...)で「A1」や「XFD1」のようなセル参照文字列を作り、SUBSTITUTE(...)で邪魔な行番号の「1」を消す、という処理をしています。
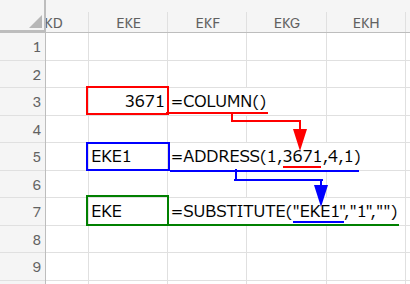
これで1行目には、私たちが目指すべきゴールがすべて表示されました。
ステップ1：ロジックの心臓部 – CHAR関数とCODE関数の関係
さて、一体どうやって数値（列番号）を文字（アルファベット）に変換するのでしょうか？
今回の冒険の主役は、CHAR関数です。
CHAR関数は、コンピュータの世界で文字に割り当てられている「コード番号」を指定すると、その番号に対応する文字を返してくれる、まるで翻訳機のような関数です。
では、私たちが欲しいアルファベットの「A」（大文字である点に注目してください！）のコード番号は何番なのでしょう？
それを調べるには、CHAR関数の相棒であるCODE関数が使えます。
=CODE("A")
この数式は、「65」という答えを返します。そう、Aのコード番号は65番なのです。
同様に、Zは90番です。
ということは…？
「65から始まる連続した数値を作り、それをCHAR関数に渡せば、アルファベットが順番に出てくるのでは？」
その通り！この閃きが、すべての謎を解くカギとなります。
ステップ2：列文字を桁ごとに分解して生成する
ここからは、列文字を「1桁目」「2桁目」「3桁目」と、桁ごとに分解して考えていきます。
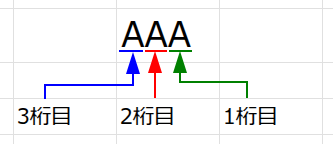
1桁目の生成（A～Zの美しい周期）
考えかた
まず、一番右側の「1桁目」の文字から考えましょう。
A, B, C, …, Z, A, B, … というように、AからZまでの26文字が、単純に繰り返されています。
このような「周期的な繰り返し」を計算するのは、ある関数の得意分野だと思いませんか？
そう、「割り算の余り」を求めるMOD関数の出番です。
数式と解説
A4セルに「1桁目」と入力し、その下のA5セルに以下の数式を入力して、右端までフィルコピーします。
=CHAR(MOD(COLUMN()-1,26)+65)
この数式を、内側から順に見ていきましょう。
・COLUMN(): まず、COLUMN関数が、数式が入力されているセルの列番号（A列なら1, B列なら2…）を返します。
・COLUMN()-1: 次に、その列番号から1を引きます。これは、計算の都合上、数を1からではなく0から（0, 1, 2…）始めたいからです。
・MOD(..., 26): そして、MOD関数が、この数を26で割った「余り」を計算します。これにより、0, 1, 2, ..., 24, 25, 0, 1, ... という、0から25までの数値が周期的に繰り返される配列が生まれます。
・... + 65: この0から25の周期的な数値に、Aのコード番号である「65」を足します。
すると、65, 66, 67, ..., 90, 65, 66, ... という、AからZのコード番号が繰り返される配列に変わります。
・CHAR(...): 最後に、CHAR関数がこのコード番号を文字に翻訳し、見事に1桁目のアルファベットが表示される、というわけです。
2桁目の生成（26列ごとの新たな周期）
考えかた
1桁目より少し複雑になりますね。
2桁目は、最初の26列（A～Z列）までは空白で、27列目（AA列）から初めて「A」が登場します。
そして、そこから26列ごとに「B」「C」…と変化していきます。
「N個ごとに1つ進む」という計算は、「割り算の商」を求めるQUOTIENT関数の得意分野です。
数式と解説
A8セルに「2桁目」と入力し、その下のA9セルに以下の数式を入力して、右端までフィルコピーします。
=IF(COLUMN()<=26,"",CHAR(MOD(QUOTIENT(COLUMN()-COLUMN($AA$1),26),26)+65))
これも内側から見ていきましょう。
・IF(COLUMN()<=26,"", ...): まず、IF関数が門番の役割をします。「もし列番号が26以下（Z列まで）なら、空白（””）を表示しなさい。そうでなければ、右側の計算をしなさい」と命令しています。
・COLUMN()-COLUMN($AA$1): ここがポイントです。COLUMN($AA$1)は「27」という数値を返します。
現在の列番号から27を引くことで、AA列を「0」番目として計算をリセットしています。（AA列なら27-27=0, AB列なら28-27=1…）
・QUOTIENT(..., 26): このリセットされた数値を、26で割った「商」を求めます。
これにより、0,0,...,0 (26個), 1,1,...,1 (26個), ... という、26列ごとに1つずつ増える数値の配列が生まれます。
・MOD(..., 26)+65 と CHAR(...): あとは1桁目と同じです。この商をさらにMODで周期計算し、65を足してCHAR関数に渡すことで、26列周期でA, B, C…と変化する2桁目の文字が完成します。
3桁目の生成（周期を考えない、よりシンプルなロジック）
考えかた
いよいよ3桁目です。3桁目が登場するのは、2桁目がZになった次の列、つまりAAA列（703列目）からですね。
ここで一つ、面白い事実があります。Excelの最大列数は16384列でしたね。
アルファベット26文字の3乗は 26^3 = 17576 です。
つまり、Excelの列は、3桁目がAからZまで一周する前に終わってしまうのです！
ということは…3桁目には、1桁目や2桁目のような「周期」を考える必要がないのでは？
その通り！そのため、MOD関数が不要になり、ロジックはむしろシンプルになります。
数式と解説
A12セルに「3桁目」と入力し、その下のA13セルに以下の数式を入力して、右端までフィルコピーします。
=IF(COLUMN()<=COLUMN($ZZ$1),"",CHAR(QUOTIENT(COLUMN()-COLUMN($AAA$1),26^2)+65))
・IF(COLUMN()<=COLUMN($ZZ$1),"", ...): 今回の門番は、ZZ列です。
COLUMN($ZZ$1)と書くことで、702という数値を直接書かなくても、Excelが自動で計算してくれます。702列目までは空白です。
・COLUMN()-COLUMN($AAA$1): 計算の開始点をAAA列（703列目）にするため、703を引いてリセットします。
・QUOTIENT(..., 26^2): 3桁目は、2桁目が26回一周するごとに1つ進みます。
つまり、26 * 26 = 26^2 (676)列ごとに変化します。
この商を求めることで、3桁目の文字のインデックス（Aなら0, Bなら1…）が計算できます。
・...+65 と CHAR(...): 最後に65を足してCHAR関数に渡せば、3桁目の文字が完成です。
ステップ3：完成、そして審判の時
さあ、すべての部品が揃いました。あとは、これらを結合するだけです！
3つの桁を結合する
A16セルに「連結」と入力し、その下のA17セルに以下の数式を入力して、右端までフィルコピーします。
=CONCAT(A13,A9,A5)
CONCAT関数は、引数に指定した文字列を、単純に左から順番に連結する、とてもシンプルな関数です。
3桁目、2桁目、1桁目の順（A13, A9, A5）に指定することで、それぞれの行で計算された文字が結合されます。
1桁目や2桁目しかない列では、空白が結合されるだけなので、正しく表示されますね。
【CONCAT vs TEXTJOIN】
複数の文字列を結合する関数にはTEXTJOINもありますが、TEXTJOINは区切り文字を指定する機能があります。
今回のように、単純に文字を繋げたいだけであれば、引数が少ないCONCAT関数を使う方がシンプルで、私のおすすめです！
正解との照合
ついに、審判の時が来ました。
私たちのロジックで作り上げた17行目の文字列が、最初にADDRESS関数で用意した1行目の「正解」と、16384列すべてにおいて完全に一致しているか、一括で判定しましょう。
A20セルに「照合」と入力し、その下のA21セルに、以下の数式を入力します。
=AND(EXACT(1:1,17:17))
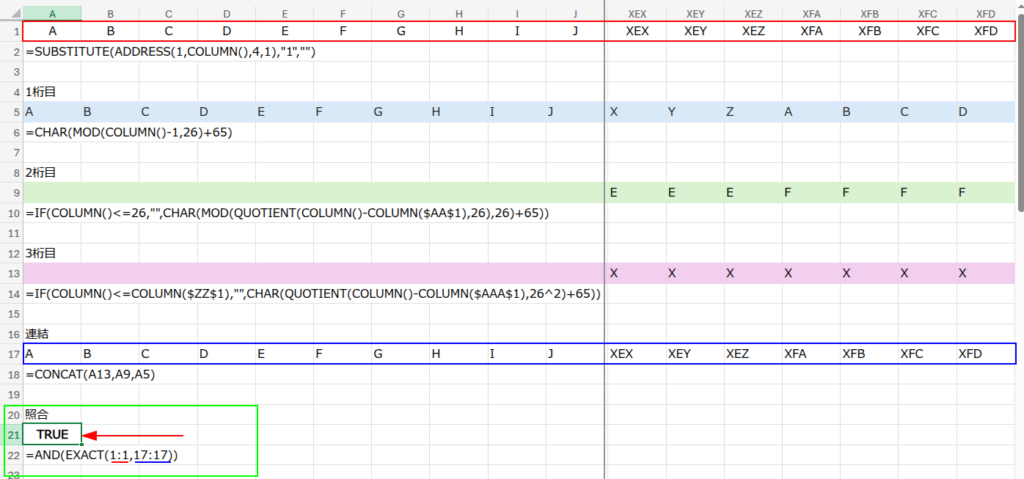
・EXACT(1:1,17:17): まず、EXACT関数が、1行目全体と17行目全体を、セルごとに比較します。EXACTは大文字と小文字を区別して比較する、厳密な関数です。
すべてのセルで一致していれば、{TRUE,TRUE,...}という、すべてがTRUEの配列を返します。
・AND(...): 最後に、AND関数が、この配列のすべての要素がTRUEであるかどうかを判定します。
一つでもFALSEがあれば結果はFALSEになりますが、すべてがTRUEであれば、最終的な答えとして「TRUE」を返します。
見事「TRUE」が表示されれば、完全成功です！
まとめ：関数リスト
今回の冒険は、いかがでしたか？
ADDRESS関数というゴールを知りながら、あえて回り道をし、その仕組みを自らの手で再構築してみました。
このプロセスを通じて、普段何気なく使っている関数たちが、いかに精巧なロジックで動いているか、その一端を感じていただけたのではないでしょうか。
最後に、今回登場した関数たちをリストアップしておきましょう。一つひとつの役割を思い返すと、今回の冒探の記憶がより深く刻まれるはずです。
- ADDRESS: 行番号と列番号から、セル参照の文字列（例：”A1″）を作成する。
- SUBSTITUTE: 文字列の一部を、別の文字列に置き換える。
- COLUMN: セルの列番号を返す。
- CHAR: コード番号に対応する文字を返す。
- CODE: 文字に対応するコード番号を返す。
- MOD: 割り算の「余り」を返す。周期的な計算が得意。
- QUOTIENT: 割り算の「商」の整数部分を返す。
- IF: 条件を判定し、真の場合と偽の場合で処理を分岐させる。
- CONCAT: 複数の文字列を単純に連結する。
- EXACT: 2つの文字列を、大文字・小文字を区別して比較する。
- AND: すべての引数がTRUEであるかどうかを判定する。
今回の「暇つぶし」が、皆さんのExcelへの知的好奇心をさらに深めるきっかけになれば幸いです。
