Excel数式アート！不思議な模様の作り方【コピペOK】

本記事では、無料のWeb版Excelを使用して検証および画像の作成を行っています。Windowsはもちろん、MacやLinuxの方もブラウザさえあれば挑戦できます！

はじめに：Excelは、無限のキャンバスだ！
今回のミッションと準備
Excel数式アート 11選
まとめ：数式は、創造の翼だ！
1. 今回登場した関数リスト

はじめに：Excelは、無限のキャンバスだ！

「Excelでできることといえば、表計算やグラフ作成でしょ？」

そう思ったあなた、大正解！

ほとんどの場合、Excelはビジネスの強力な相棒です。

でも、ちょっと待ってください！
Excelの世界は、私たちが思っているよりもずっと広く、そして自由です。

もし、Excelのマス目一つひとつが、絵を描くための「ピクセル」だとしたら？
もし、無味乾燥に見える「関数」が、絵を描くための「絵筆」だとしたら？

「え、Excelで絵を描く？しかも、数式だけで？」

そんな少し変わった挑戦を、今日、皆さんと一緒に楽しんでみたいと思います！

今回の記事は、普段ならまず使わないであろう関数の組み合わせや、数学的なロジックを駆使して、52×52のセル範囲に美しい模様を描き出す「数式アート」の世界にご招待します。

目的は、

数式の持つ論理が、どのようにして美しい模様に変わるのか、その神秘的なプロセスを体感すること！

ROW関数とCOLUMN関数がこんな幾何学模様を生むなんて！
三角関数で波を描けるのは知っていたけど、こんなパターンも作れるんだ！

きっと、そんな発見があるはずです。

もちろん、今回紹介する「■」と「□」は、あなたの好みに応じて「●」や「・」など他の記号に変えたり、条件付き書式を使って好きな色に塗り分けたりすることもできますよ！

さあ、あなたのExcelを無限のキャンバスに変える、摩訶不思議な冒険に出発しましょう！

以下の記事でも数式アートを扱っています！

今回のミッションと準備

目指すゴール： 52×52のセル範囲（A1:AZ52）に、たった1つの数式をコピーするだけで、「■」と「□」を使った幾何学模様を描き出す。

ルール：

偶然性に頼るRAND系の関数は使用しない。
ROW関数（行番号）とCOLUMN関数（列番号）を基本とした、計算ロジックだけで模様を生成する。

「なぜ条件付き書式でセルの色を塗るのではなく、わざわざ文字を使うの？」

良い質問ですね！

条件付き書式も素晴らしい機能ですが、今回のように広大な範囲（52×52=2704セル）に複雑な数式を設定すると、Excelの動作が重くなることがあります。（特にWEB版Excelでは）

今回は、より軽快に動作し、数式の結果が直接目に見える「文字」を使う方法を選びます。

「どうして52×52という、少し中途半端な範囲なの？」

これも良い視点です！Excelの列はAからZまでの26文字で一区切りですよね。

52という数字は、ちょうどそのアルファベット2周分（A～Z, AA～AZ）にあたります。

こうすることで、列の範囲を選択しやすく、キリが良いというわけなのです。

では、準備をしましょう。まず、まっさらなシートを用意し、A1セルを選択してください。

これから紹介する数式をA1セルにコピー＆ペーストし、その数式をA1:AZ52の範囲にコピーするだけで、魔法のようにアートが広がりますよ！

Excel数式アート 11選

パターン1：基本のチェック柄

考えかた

まずは肩慣らしです。

行番号と列番号を掛け算し、その結果が偶数か奇数かで色を塗り分ければ、綺麗なチェック柄ができそうですよね？

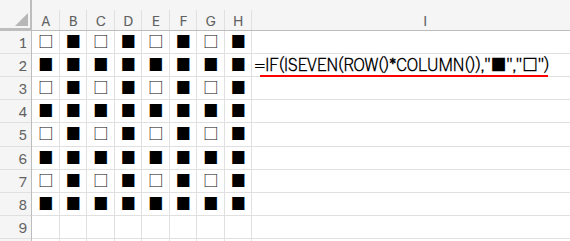
このシンプルな発想を、MOD関数を使って表現してみましょう。

数式と解説

=IF(MOD(ROW()*COLUMN(),4)>1,"■","□")

ROW()*COLUMN(): まず、行番号と列番号を掛け合わせます。これは、シート全体に巨大な「九九の表」を作るようなイメージです。
MOD(..., 4): 次に、その掛け算の結果を4で割った「余り」を求めます。余りは「0, 1, 2, 3」のいずれかになります。
IF(... > 1, "■", "□"): 最後に、もし余りが1より大きい（つまり2か3）なら「■」を、そうでなければ「□」を表示します。

これにより、計算結果に応じてセルが市松模様（とは少し違いますが…）に塗り分けられるのです。

パターン2：中心から広がる波紋

考えかた

次は、池に石を投げ込んだときに広がる、同心円状の波紋のような模様に挑戦します。

そのためには、各セルが「キャンバスの中心からどれだけ離れているか」を計算する必要があります。
そう、数学で習った「三平方の定理」の出番です！

数式と解説

=IF(MOD(SQRT(SUMSQ(ROW()-26,COLUMN()-26)),7)>4,"■","□")

ROW()-26 と COLUMN()-26: 52×52の中心（おおよそ26行目、26列目）を原点(0,0)にするため、それぞれの番号から26を引きます。
SUMSQ(...): 2つの数値の「平方和」（それぞれを2乗して足した値）を計算します。まさに三平方の定理のa² + b²の部分ですね。
SQRT(...): 平方和の「平方根」を計算します。これで、各セルと中心との「直線距離」が求まります。
MOD(..., 7) > 4: 計算した距離を7で割った余りを求め、その値に応じて■と□を配置することで、美しい波紋模様が生まれるのです。

パターン3：神秘のフラクタル模様

考えかた

ここからは少しマニアックな領域へ（笑）。

BITXOR関数という、ビット単位の排他的論理和を計算する関数を使います。

「ビット…？排他的…？」

大丈夫です！これは、行番号と列番号をそれぞれ2進数に変換し、各桁を比較して計算する、という少し変わった関数です。

このような計算は、自己相似的な図形、いわゆる「フラクタル模様」を偶然生み出すことがあるのです。

数式と解説

=IF(MOD(BITXOR(ROW(),COLUMN()),7)>3,"■","□")

BITXOR(ROW(),COLUMN()): 各セルの行番号と列番号でビット単位の計算を行います。結果は、一見ランダムに見える不思議な数値の並びになります。
MOD(..., 7) > 3: その不思議な数値を、MOD関数で規則的に塗り分けることで、まるで古代遺跡の壁画のような、複雑で美しい模様が浮かび上がります。

パターン4：最小公倍数が描くグリッド

考えかた

次は、算数で習った「最小公倍数」を使ってみましょう。

LCM関数は、2つ以上の数値の最小公倍数を返します。

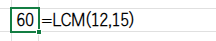
行番号と列番号の最小公倍数は、規則的なグリッド線のようなパターンを描き出します。

数式と解説

=IF(LCM(ROW(),COLUMN())>52,"□","■")

LCM(ROW(),COLUMN()): 各セルの行番号と列番号の最小公倍数を計算します。
IF(... > 52, "□", "■"): 計算結果が52より大きいかどうかで色を分けます。
これにより、数値が小さい（公約数が多い）行や列が強調され、独特な美しい模様が生まれます。

パターン5：回転するチェック柄

考えかた

パターン1で作ったチェック柄を、斜めに回転させてみましょう！

そのためには、三角関数（COS, SIN）を使った「座標回転」という少し高度な数学のテクニックを使います。

数式は複雑に見えますが、やっていることはシンプルです。

数式と解説

=LET(a,11,b,25,c,12,d,16,e,RADIANS(b),f,COS(e),g,SIN(e),h,COLUMN()-c,i,ROW()-d,j,h*f-i*g,k,h*g+i*f,IF(MOD(INT(j/a)+INT(k/a),2)=0,"■","□"))

LET関数で、数式に使う値に名前をつけています。

a～d: 模様のサイズや中心位置の調整値です。
e, f, g: 回転角度を計算しています。bの「25」が回転角度（度）です。
h, i: 中心の座標を移動させています。
j, k: ここが座標回転の心臓部。三角関数を使って、各セルの座標をぐるりと回転させています。
IF(...): 最後に、回転後の新しい座標を使って、パターン1と同じようなチェック柄を描いているのです。

パターン6：ローマ数字の複雑なテクスチャ

考えかた

ROMAN関数という、数値をローマ数字（I, V, Xなど）に変換する、少し変わった関数を使ってみましょう。
ローマ数字の「文字数」は、元の数値に対して非常に不規則に変化します。

この不規則性を利用して、面白いテクスチャを生み出します。

数式と解説

=IF(MOD(LEN(ROMAN(MOD(ABS(ROW()*ROW()-COLUMN()*COLUMN()),3999)+1)),3)=0,"■","□")

ABS(ROW()*ROW()-COLUMN()*COLUMN()): 双曲線と呼ばれるカーブを描く数値の配列を生成します。
MOD(..., 3999)+1: ROMAN関数が扱える数値の範囲（1～3999）に収めます。
LEN(ROMAN(...)): 数値をローマ数字に変換し、その「文字数」を数えます。
MOD(..., 3)=0: 文字数を3で割った余りが0になる場所だけを「■」にすることで、古代の石版のような、複雑で味わい深い模様が完成します。

パターン7：統計関数が描くオーガニックな波

考えかた

STDEV.P（標準偏差）という、統計で使う関数をアートに応用してみましょう。

以下の記事で偏差値の求め方について解説しています！

本来の目的とは全く違う使い方ですが、行番号や列番号、そして三角関数を混ぜて計算させることで、予測不能な面白い結果が生まれます。

数式と解説

=IF(MOD(INT(STDEV.P(ROW(), COLUMN(), SIN(ROW()/5)*20, COS(COLUMN()/8)*20)), 5)=0, "■", "□")

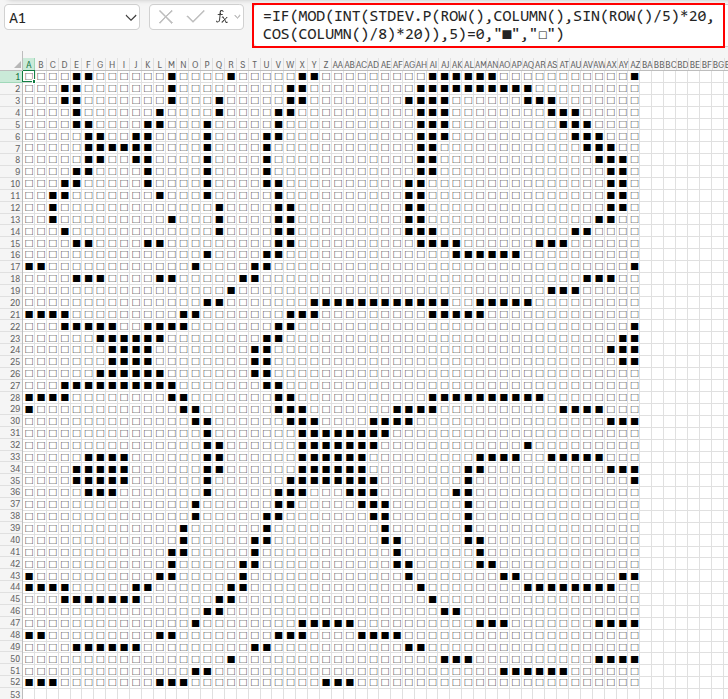
STDEV.P(...): 行番号、列番号、そしてSINとCOSが作る波の数値をまとめて標準偏差にかけます。
統計的には無意味な計算ですが、結果として複雑な数値の配列が生成されます。
MOD(INT(...), 5)=0: その複雑な結果を整数にし、5で割った余りが0になる場所を塗りつぶすことで、まるで顕微鏡で見た微生物のような、有機的なパターンが生まれます。

パターン8：調和平均が作る滑らかな模様

考えかた

これも統計関数の一つ、HARMEAN（調和平均）を使います。

調和平均は、複数の数値の逆数の平均の、さらに逆数を取るという計算で、滑らかな平均値を出すのが特徴です。

この「滑らかさ」が、アートにも活きてきます。

数式と解説

=IF(HARMEAN(ABS(SIN(ROW()/8))+0.1, ABS(COS(COLUMN()/12))+0.1, ABS(SIN((ROW()-COLUMN())/10))+0.1)<0.5, "■", "□")

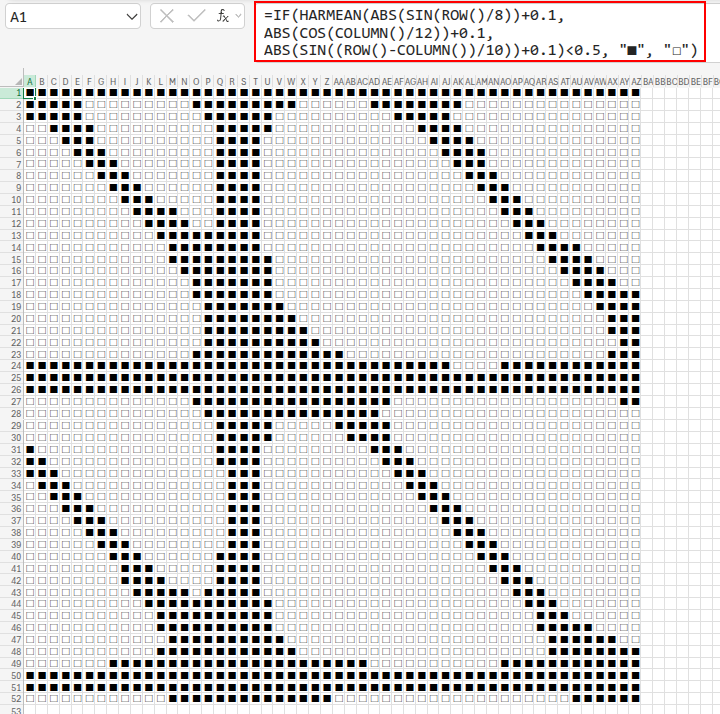
ABS(SIN(...))+0.1, ABS(COS(...))+0.1: いくつかの周期が異なる波を合成します。（0.1を足しているのは、計算エラーを防ぐためのおまじないです）
HARMEAN(...): 合成された波を、調和平均で「滑らかに」混ぜ合わせます。
... < 0.5: その滑らかな結果が、0.5より小さいかどうかで色を分けることで、独特な模様が描かれます。

パターン9：タンジェントの鋭い切れ込み

考えかた

三角関数の中でも、TAN（タンジェント）は、特定の値で無限大に発散するという、非常に「尖った」性質を持っています。

この鋭い性質を利用して、シャープで角ばった模様を描いてみましょう。

数式と解説

=IF(TAN(ROW()/12+COLUMN()/20)>TAN(ROW()/20-COLUMN()/12),"■","□")

TAN(ROW()/12+COLUMN()/20) と TAN(ROW()/20-COLUMN()/12): 異なる周期を持つ2つのタンジェントの波を生成します。
... > ... : この2つの波の大きさを比較します。
タンジェントのグラフが持つ急峻なカーブと不連続な性質により、その境界線は非常にシャープな直線となり、このようなモダンアートのような模様が生まれるのです。

パターン10：疑似乱数ノイズ

考えかた

RAND関数は禁止ですが、それっぽく見える「疑似乱数」なら作ることができます。

これは、一見ランダムに見えるけれど、実は計算に基づいているため、何度やっても同じ結果になるノイズ模様です。

秘密は、小数点以下の部分を取り出すテクニックにあります。

数式と解説

=IF(MOD(SIN(ROW()*12.9898+COLUMN()*78.233)*43758.5453,1)>0.5,"■","□")

SIN(...): まず、SIN関数で行番号と列番号を元に、滑らかな波を作ります。
... * 43758.5453: その結果に、非常に大きな、そして半端な数を掛け合わせます。これにより、値が大きく引き伸ばされ、複雑化します。
MOD(..., 1): ここが最大のポイント！数値を「1」で割った余りを求めることで、結果の「小数点以下の部分」だけを抜き出します。この操作は、元の数値の規則性を破壊し、0から1の間にランダムのように見える値を生成します。
... > 0.5: その疑似乱数が0.5より大きいかどうかで色を分けることで、テレビの砂嵐のようなノイズ模様が完成します。

パターン11：対数が描く等高線

考えかた

最後に、LOG（対数）を使ってみましょう。対数もまた、滑らかな非線形のカーブを描く関数です。

異なる周期の波をLOG関数に通し、その大小を比較することで、まるで地形図の等高線のような、有機的な模様が生まれます。

数式と解説

=IF(LOG(1.1+SIN(ROW()/8)*COS(COLUMN()/5)) > LOG(1.1+SIN(COLUMN()/8)*COS(ROW()/5)),"■","□")

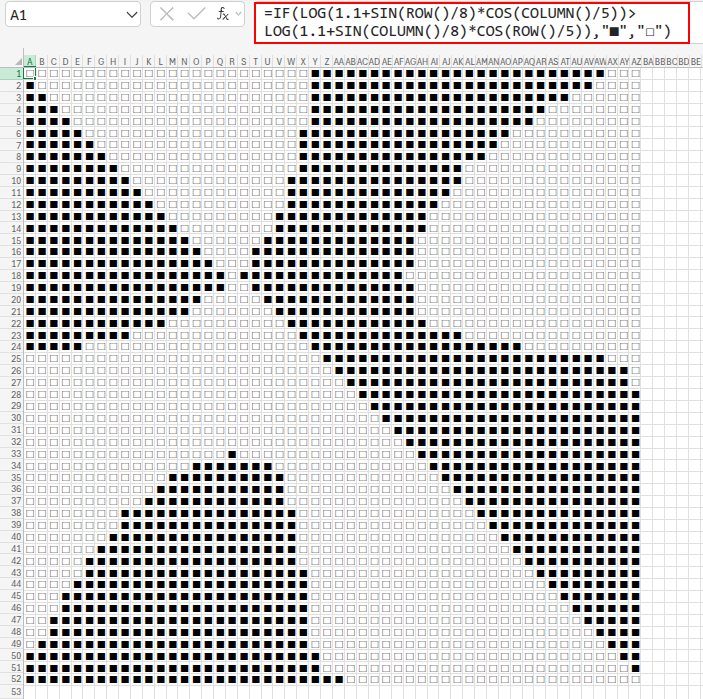
1.1+SIN(...)*COS(...): 周期の異なるSINとCOSを掛け合わせることで、複雑な波を2種類作ります。（1.1を足しているのは、LOG関数が正の数しか扱えないためのおまじないです）
LOG(...) > LOG(...): 2つの複雑な波を、それぞれLOG関数でさらに滑らかに変換し、その大小を比較します。
結果として、滑らかな曲線が複雑に絡み合った、美しい等高線のようなアートが生まれるのです。