本記事では、無料のWeb版Excelを使用して検証および画像の作成を行っています。Windowsはもちろん、MacやLinuxの方もブラウザさえあれば挑戦できます！
はじめに：Excelは、アートのキャンバスだ！
「Excelのグラフといえば、棒グラフや円グラフでしょ？」
そう思ったあなた、大正解！
ほとんどの場合、Excelのグラフは、データを分かりやすく見せるための強力なツールです。
でも、ちょっと待ってください！
もし、グラフを「データを表示するもの」ではなく、「図形を描くためのキャンバス」として捉え直したら、どうなるでしょう？
「え、Excelのグラフで絵を描く？関数を使って？」
そんな、いつものExcelがアートツールに変わる、少し変わった挑戦をしてみませんか？
今回の記事は、Excelの「散布図グラフ」と、いくつかの基本的な関数を組み合わせて、美しい図形を描き出す方法を、初心者の方にも分かりやすく解説する「初級編」です。
数学の知識とExcelの機能が融合する、クリエイティブな世界を一緒に楽しみましょう！
※他にも、関数で模様などを描く記事を投稿しています。
Excel数式アート！簡単モザイク模様の作り方【初心者向け】
次回予告
今回の初級編をマスターすれば、あなたも立派なグラフアーティストの仲間入り！
次回以降「中級編」では、このテクニックを応用して、ハートマークをはじめとする、より複雑で美しい図形にも挑戦する予定です。お楽しみに！
Web版Excelをお使いの方へ
今回の図形描画では、グラフの縦と横の比率が1:1に近くなるように見せることが重要です。
無料のWeb版Excelでは、グラフの縦横比を手動で調整する必要があります。
グラフエリアの角をドラッグして、図形が綺麗な正方形や円に見えるように、適宜調整しながら進めてくださいね！
ステップ1：基本のキ – グラフで「正方形」を描こう
何事も、まずは基本から。一番シンプルな図形、「正方形」を描くことから始めましょう。
考えかた
今回主役となる「散布図グラフ」とは、一体どんなグラフなのでしょうか？
散布図は、縦軸と横軸を持つ座標平面上に、データの点（プロット）を配置して、2つの項目の関係性を見るためのグラフです。
そして、いくつか種類がある中で、私たちが今回使う「散布図（直線）」は、とても素直なヤツです。
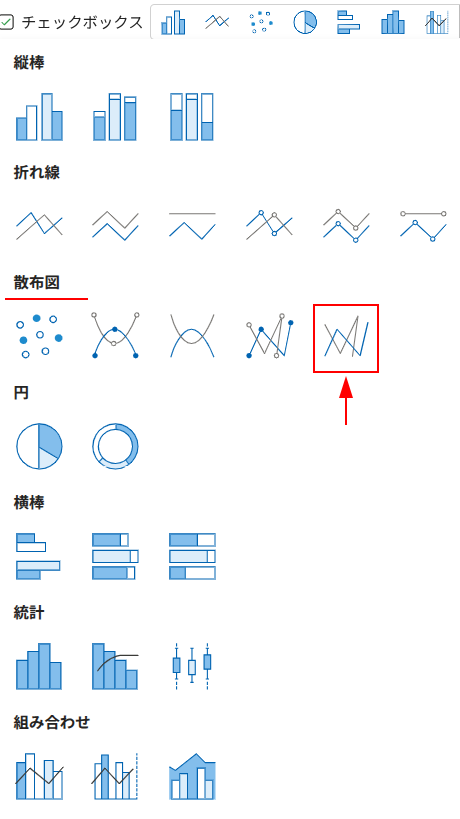
指定したXとYの座標の点を、リストの上から順番に、まっすぐな線で結んでくれる。
ただそれだけです。
ということは、正方形の4つの頂点と、最後にスタート地点に戻る座標さえ教えてあげれば、Excelは忠実に正方形を描いてくれるはずですよね？
手順
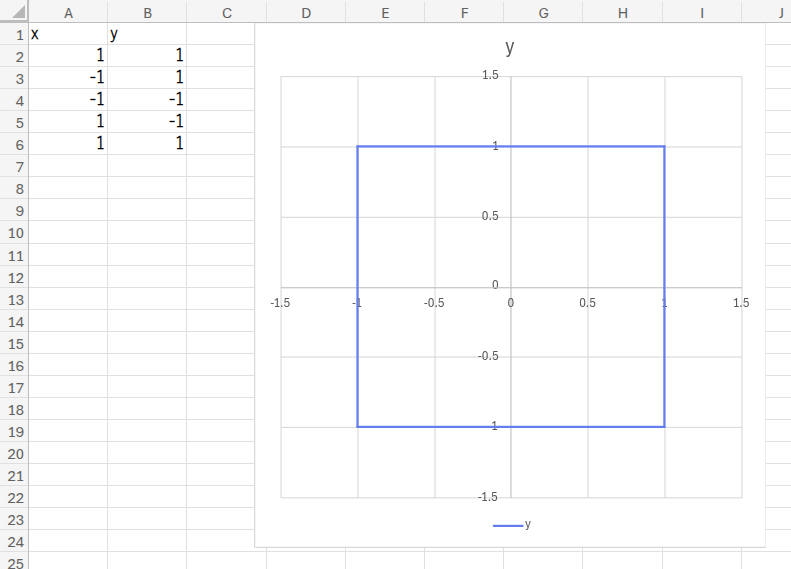
まず、まっさらなシートのA1セルに「x」、B1セルに「y」と入力します。
そして、その下に、正方形の頂点となる以下の座標データを入力してください。
={"x","y";1,1;-1,1;-1,-1;1,-1;1,1}
この数式をA1セルに貼り付けます。
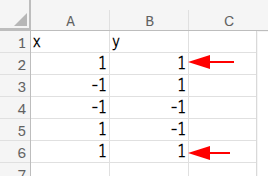
ポイントは、スタート地点である(1, 1)に、最後にもう一度戻ってくることです。
こうしないと、図形が閉じて綺麗な四角になりませんよ！
データが入力できたら、A1セルからB6セルまでの範囲をすべて選択します。
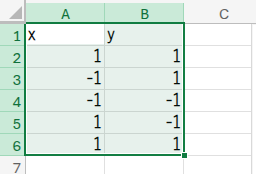
次に、リボンの「挿入」タブから「グラフ」→「散布図」→「散布図（直線）」を選択します。
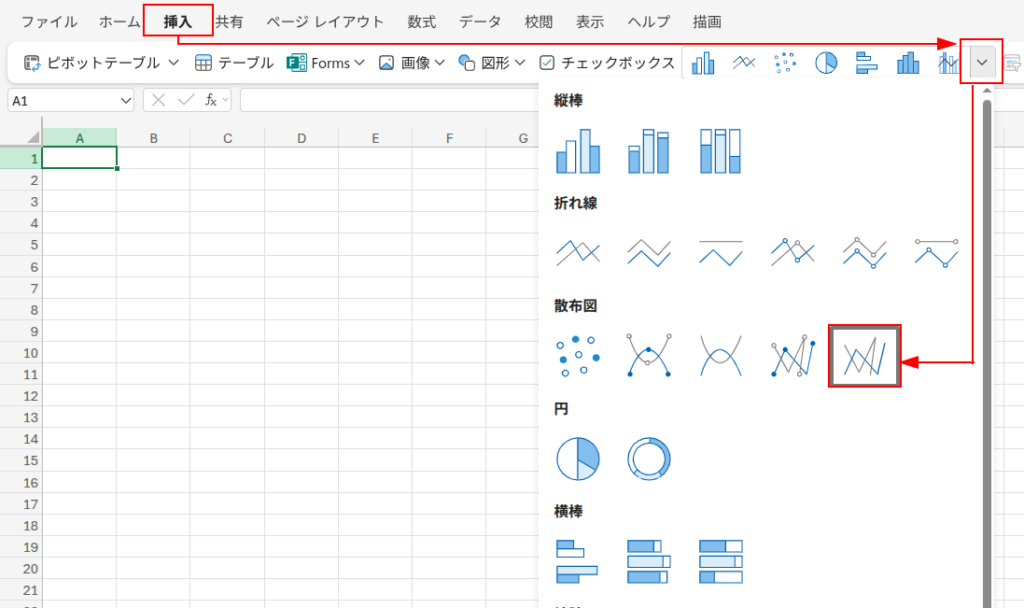
どうでしょう？あっという間に、美しい正方形が描かれました！
これが、数式で図形を描くための、最も基本的な第一歩です。
ステップ2：三角関数の魔法 – 「正多角形」を描こう
正方形が描けたなら、次は正六角形、正十三角形…と、もっと複雑な図形に挑戦したくなりますよね？
でも、頂点の座標をいちいち手で入力するのは大変です。
「もっとスマートに、数式だけで描けないの？」
もちろんできます！ここで、学生時代に私たちを少し悩ませた（？）、あのヒーローたちの出番です。そう、三角関数COS（コサイン）とSIN（サイン）です！
COSとSINを思い出そう！
「三角関数…なんだか難しかった記憶が…」という方もご安心ください！
今回使う知識は、たった一つです。
「半径1の円（単位円）があったとき、中心からある角度の線を引くと、その円周上の点のX座標がCOS、Y座標がSINになる」
ただこれだけです！
つまり、角度さえ指定してあげれば、COSとSINが円周上の座標を自動で計算してくれる、というわけです。
これを使えば、どんな正多角形でも描けそうですよね？
正六角形を描いてみよう
新しいシートを用意してください。
A1セルに「角度」と入力し、A2セルに以下の数式を入力します。
=SEQUENCE(6+1,,0,360/6)
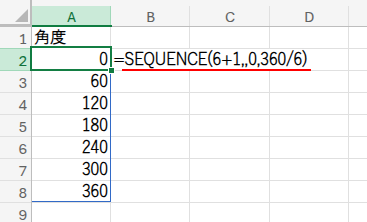
この数式は、正六角形の頂点の「角度」を計算しています。
・360/6: 円の一周（360度）を6等分して、中心角（60度）を求めます。
・SEQUENCE(6+1, ,0, ...): 0度からスタートして、60度ずつ、7個（6+1）の連続データを作ります。最後の「+1」が、スタート地点に戻ってきて図形を閉じるための、重要なおまじないです！
次に、B1セルに「x」、C1セルに「y」と入力し、それぞれに以下の数式を入力します。
B2セル: =COS(RADIANS(A2#))
C2セル: =SIN(RADIANS(A2#))
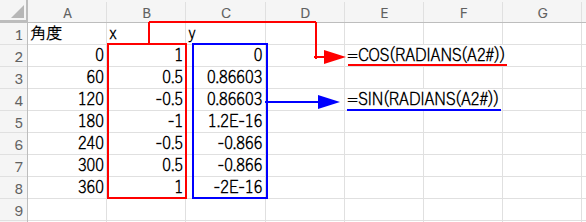
・RADIANS(A2#): COSやSIN関数は角度を「ラディアン」という単位で計算するので、RADIANS関数で私たちが慣れている「度」から変換します。
「A2#」という書き方は、A2セルから始まるスピル範囲全体を参照するという意味です。
・COS(...)とSIN(...): 角度からX座標を求めるのがCOS、Y座標を求めるのがSINの役割です。これで、円周上の各頂点の座標が自動で計算されます。
あとは簡単！B列とC列のデータ範囲をすべて選択し、先ほどと同じように「散布図（直線）」グラフを挿入してください。
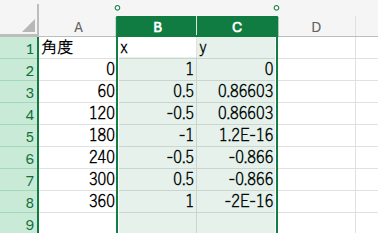
縦横比を調整すれば…ほら、綺麗な正六角形がそこに！
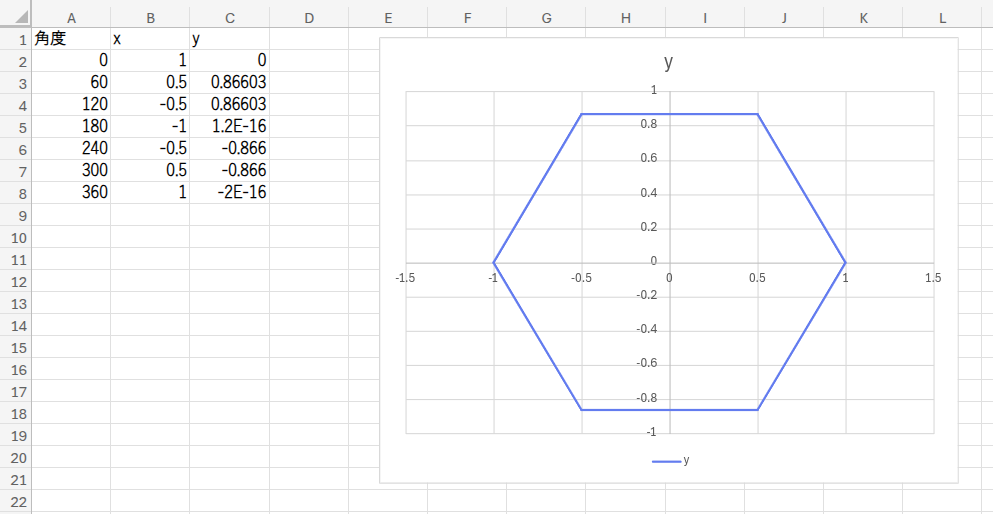
数値を書き換えるだけで…？
この方法のすごいところは、数式を変えるだけで、どんな正多角形でも描けてしまうことです。
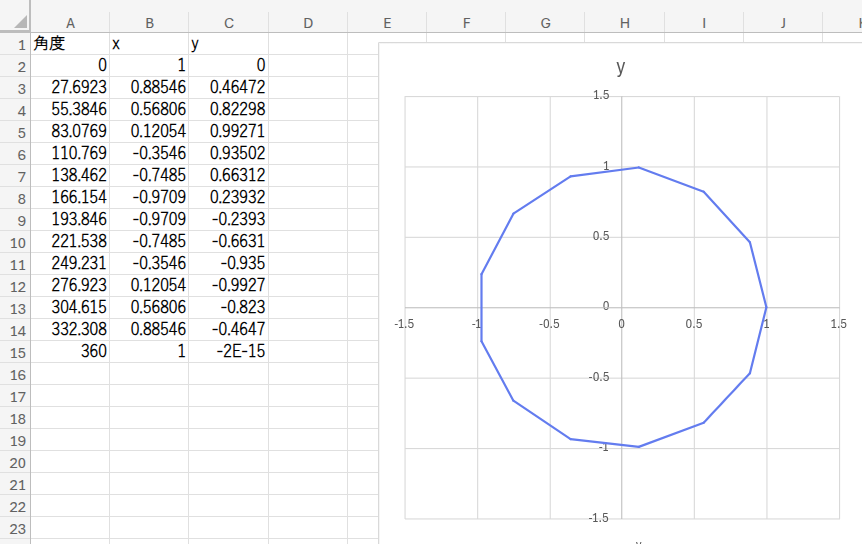
試しに、A2セルの数式を、=SEQUENCE(13+1,,0,360/13) に書き換えてみてください。
どうでしょう？数値を書き換えただけで、グラフが瞬時に「正十三角形」に変わりました！これが、数式で図形を描くことの面白さなのです。
ステップ3：頂点を増やせば…「円」になる！
「正六角形、正十三角形…と頂点の数をどんどん増やしていったら、最終的にどうなるんだろう？」
素晴らしい疑問です！その答えは、皆さんがご存知の通り「円」です。
では、思い切って「正360角形」を描いて、限りなく円に近い図形を作ってみましょう！
手順
新しいシートを用意し、A1セルに「x」、B1セルに「y」と入力します。
今回は、角度の作業列を作らず、直接XとYを計算してみましょう。
A2セル: =COS(RADIANS(SEQUENCE(361,,0)))
B2セル: =SIN(RADIANS(SEQUENCE(361,,0)))
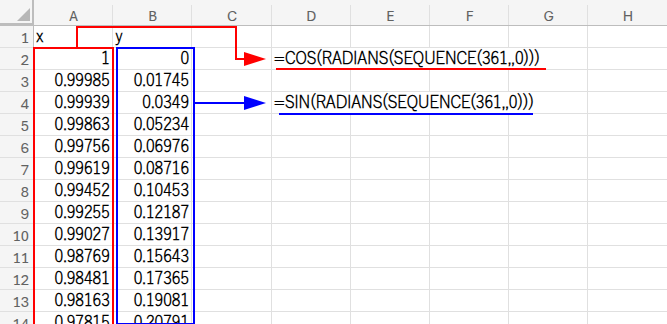
SEQUENCE(361,,0)が、0度から360度までの361個の角度を直接作り出しています。
準備ができたら、A列とB列のデータ範囲をすべて選択して、先ほどと同じようにグラフ化すれば…
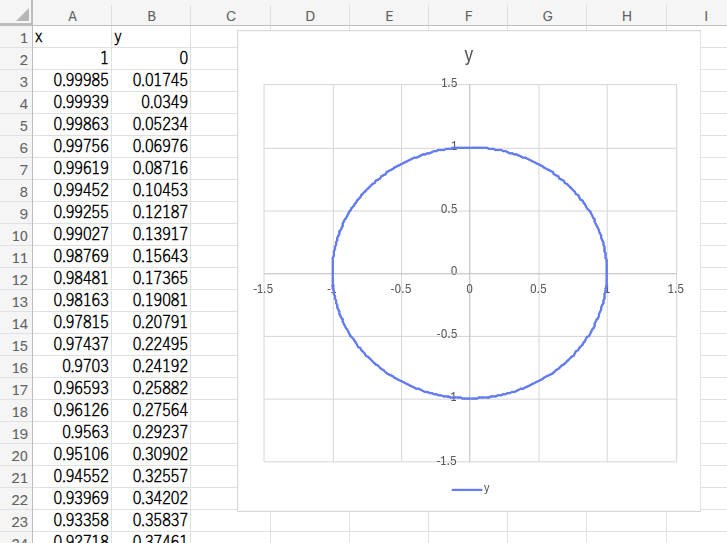
完璧な円が描けましたね！
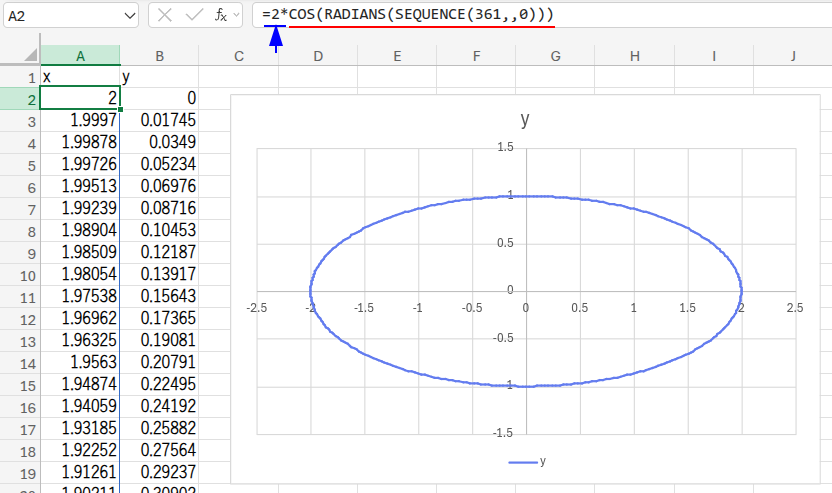
ちなみに、楕円を描きたい場合は、例えばA2セルの数式を =2*COS(...) のように、COSかSINのどちらかに係数を掛けてあげるだけで、簡単に描くことができますよ。試してみてください！
ステップ4：三角関数の真骨頂 – 美しい「波」を描こう
さて、COSとSINが円を描くのを見て、「三角関数といえば波だ！」と思った方もいるのではないでしょうか？
その通り！円周上をぐるぐる回る動きを、横に広げて見てみると、それは美しい波になるのです。
手順
新しいシートを用意します。
A1セルに「x」と入力し、A2セルに=SEQUENCE(1000)と入力して、X軸の値を1000まで用意します。
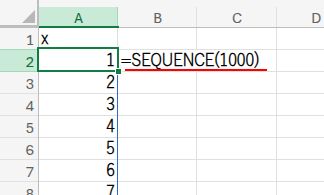
B1セルに「cos」、C1セルに「sin」と入力し、それぞれ以下の数式を入れます。
B2セル: =COS(RADIANS(A2#))
C2セル: =SIN(RADIANS(A2#))
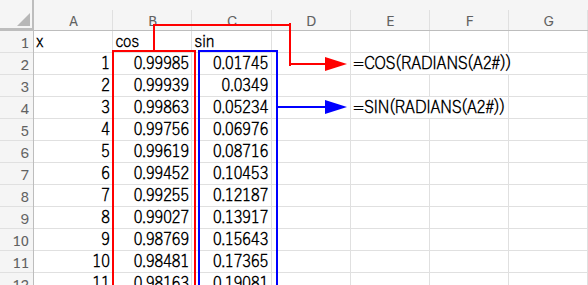
入力できたら、今度はA列からC列まで、3列すべてを選択して、「散布図（直線）」を挿入してください。
「なぜ、今度は3列も選択するの？」
それは、Excelが「最初の列を共通のX軸、2番目以降の列をそれぞれ別のY軸のデータ（データ系列）として扱ってくれる」からです。
これにより、1つのグラフにCOSの波とSINの波、2つのグラフを同時に描くことができるのです。
どうでしょう？COSの波とSINの波が、少しだけズレて表示される、美しいグラフが描かれました。
これが三角関数の本来の姿なのです。
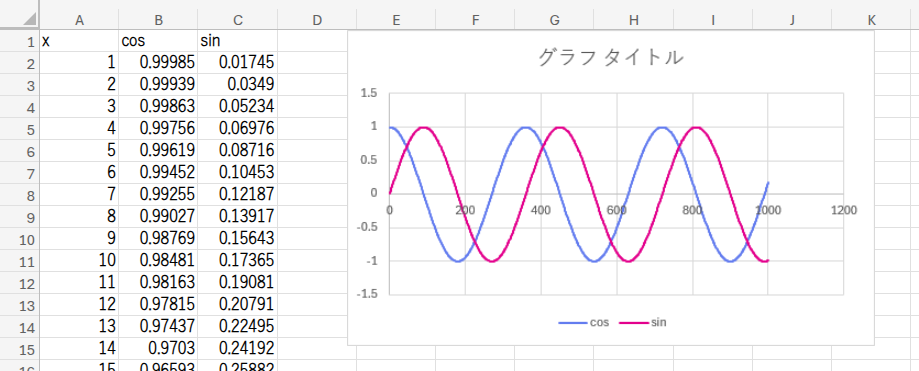
ステップ5：暇つぶしの極み – 「螺旋」を描こう
さあ、初級編の最後を飾るのは、まさに「Excelで暇つぶし」にふさわしい、少し変わった関数を使った「螺旋」模様です！
本来、螺旋を描くのに複素数関数を使う必要は全くありません。
でも、そこは「Excelで暇つぶし」！あえて、普段使わない関数を使ってみることにロマンがあるじゃないですか！
高校数学で、三角関数と複素数といえば、多くの人が苦戦した「中ボス」級の単元だったのではないでしょうか。
この記事を読んで、「ああ、こんなことやったなぁ」と懐かしい気持ちになっていただけたら嬉しいです。
複素数については以下の記事でも無駄に扱っています。
手順
新しいシートを開きます。
まず、角度と、螺旋の「半径」を用意します。
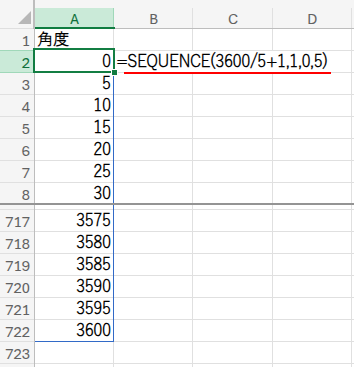
A1セルに「角度」、A2セルに=SEQUENCE(3600/5+1,1,0,5)と入力します。
これで0度から3600度（10周分！）まで、5度刻みの角度ができます。
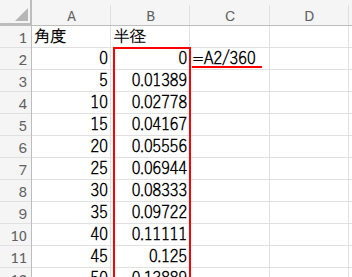
B1セルに「半径」、B2セルに=A2/360と入力し、下までフィルコピーします。
これが螺旋のキモ！角度が大きくなるにつれて、半径も少しずつ大きくなっていく、という仕掛けです。
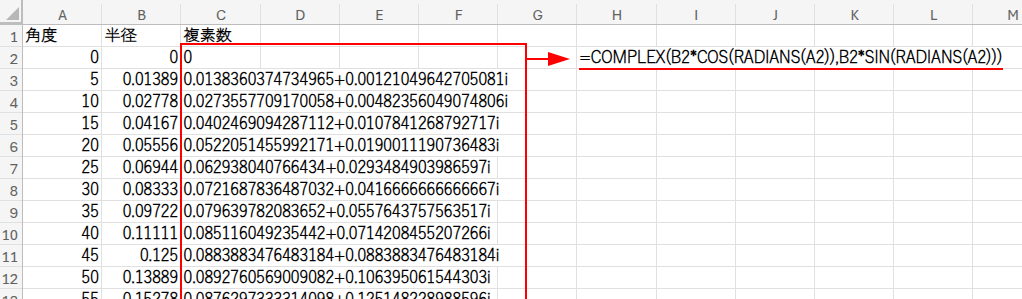
C1セルに「複素数」と入力し、C2セルに以下の数式を入れ、フィルコピーします。
=COMPLEX(B2*COS(RADIANS(A2)),B2*SIN(RADIANS(A2)))
COMPLEX関数は、X座標（実部）とY座標（虚部）を一つの「複素数」にまとめてくれる関数です。
半径を考慮したX座標とY座標を、ここで一つの数値にパッケージングしています。
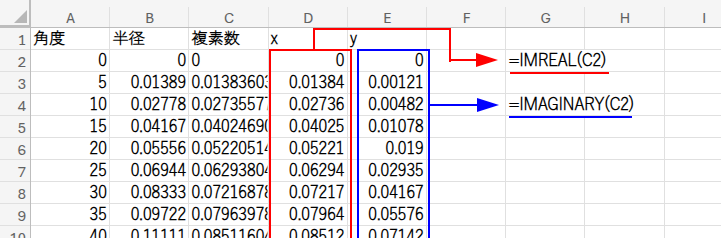
最後に、この複素数からXとYを再び取り出します。
D1セルに「x」、D2セルに=IMREAL(C2)（複素数の実部を取り出す）
E1セルに「y」、E2セルに=IMAGINARY(C2)（複素数の虚部を取り出す）
と入力し、それぞれフィルコピーします。
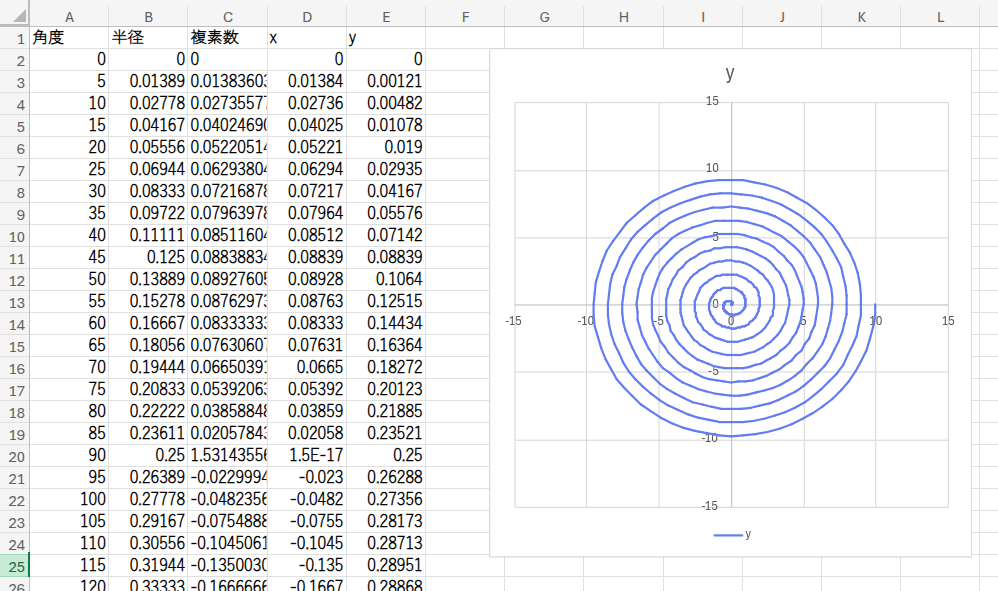
準備は整いました！D列とE列をすべて選択し、「散布図（直線）」グラフを挿入してください。
そこには、中心から外へ向かって広がる、美しい螺旋模様が描かれているはずです！
まとめ：Excelは、数学とアートの交差点だ！
単純な正方形から始まり、正多角形、円、波、そして美しい螺旋まで。
Excelのグラフ機能と、基本的な関数たちが、いかにクリエイティブな可能性を秘めているか、感じていただけたのではないでしょうか。
数式を組み立てる論理的な楽しさと、それが美しい図形として現れる視覚的な楽しさ。Excelは、まさに数学とアートが交差する、最高の遊び場なのです。
最後に、今回登場した関数たちをリストアップしておきましょう。
今回登場した関数リスト
- SEQUENCE(行, [列], [開始], [ステップ]): 連続した数値の配列を生成します。[行]に作りたい数値の個数を指定します。
- COS(数値): 角度（ラジアン単位）からX座標を求める三角関数です。[数値]にラジアンの角度を指定します。
- SIN(数値): 角度（ラジアン単位）からY座標を求める三角関数です。[数値]にラジアンの角度を指定します。
- RADIANS(角度): 角度の単位「度」を「ラジアン」に変換します。[角度]に度単位の数値を指定します。
- COMPLEX(実部, 虚部, [接尾辞]): X座標（実部）とY座標（虚部）から「複素数」を作成します。
- IMREAL(複素数): 複素数からX座標（実部）を取り出します。
- IMAGINARY(複素数): 複素数からY座標（虚部）を取り出します。
さあ、基本はマスターしましたね？
次回、「中級編」では、いよいよ、より複雑な図形、あの「ハートマーク」の描画に挑戦します！
今回のテクニックをどう応用すれば描けるのか、ぜひ考えてみてくださいね。お楽しみに！
