本記事では、無料のWeb版Excelを使用して検証および画像の作成を行っています。Windowsはもちろん、MacやLinuxの方もブラウザさえあれば挑戦できます！
はじめに：ただの連番じゃ、つまらない！
「Excelで連番を作るなら、フィルハンドルをドラッグでしょ？」
そう思ったあなた、大正解！
ほとんどの場合、それが最も簡単で分かりやすい方法です。
でも、ちょっと待ってください！
もし、ただまっすぐに並んだ連番ではなく、こんなふうに…左右に揺れる「ジグザグの連番」を作りたくなったら、どうしますか？
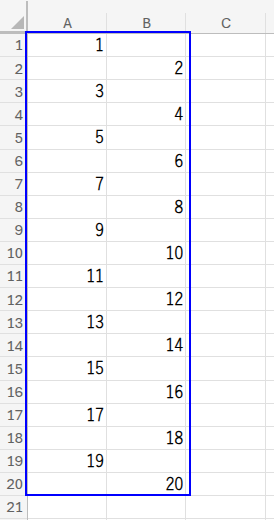
「え、こんなのどうやって作るの？手作業で一個ずつ入力するの？」
そんな退屈なことはさせません！今回の記事は、この美しいジグザグ模様を、Excelの「数式」だけで作り出す、思考のパズルです。
古典的なテクニックから、最新の強力な関数まで、なんと9種類ものアプローチでこの問題に挑みます。
目的は、
同じゴールに対して、いかに多くの道筋が存在するかを知り、Excelの柔軟性と表現力の豊かさを体感すること！
きっと、「こんな関数あったんだ！」「こんな使い方ができるなんて！」という発見があるはずです。
今回は、分かりやすさを重視して、1から20までの連番をA1:B20の範囲に作成することに挑戦します。
さあ、あなたのExcel関数への理解がさらに深まるかもしれない、楽しい冒険に出発しましょう！
Part 1：いにしえの技 – フィルコピーで作るジグザグ
まず、Excelの古き良き時代から伝わる、数式をコピーしていく方法です。
スピル機能がなかった頃、先人たちはこのような知恵で問題を解決していました。
しかし、このような配列を作ることはなかったと思います。笑
アプローチ1：IF + MOD（王道の論理パズル）
考えかた
ジグザグ模様は、言い換えれば「市松模様（チェッカーボード）」の位置に数字を配置することですよね。
つまり、セルの「行番号」と「列番号」が、それぞれ偶数か奇数かを判定すれば、この市松模様のロジックは作れそうです。
「奇数行・奇数列」と「偶数行・偶数列」の場所にだけ数字を置く、というルールを数式で表現してみましょう！
数式と解説
A1セルに、以下の数式を入力します。
=IF(MOD(ROW(A1),2)=MOD(COLUMN(A1),2),ROW(A1),"")
入力したら、この数式をA1:B20の範囲にコピーしてください。
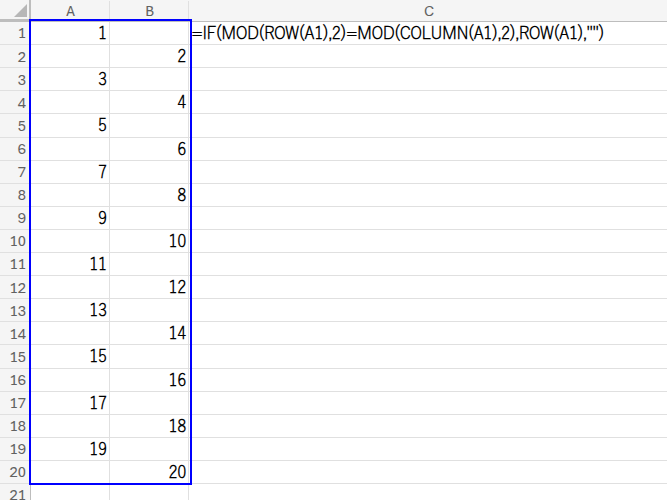
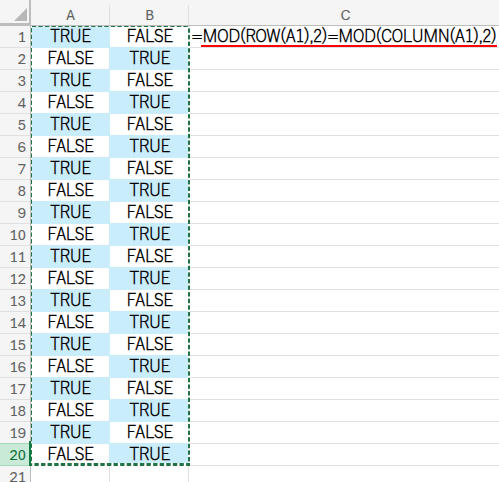
この数式の心臓部は、MOD(ROW(A1),2)=MOD(COLUMN(A1),2) の部分です。
・MOD(ROW(A1),2): 行番号を2で割った余りを求めます。奇数行なら「1」、偶数行なら「0」が返ります。
・MOD(COLUMN(A1),2): 列番号を2で割った余りを求めます。A列（1列目）は「1」、B列（2列目）は「0」です。
・... = ...: この二つの結果が等しいかどうかを判定します。
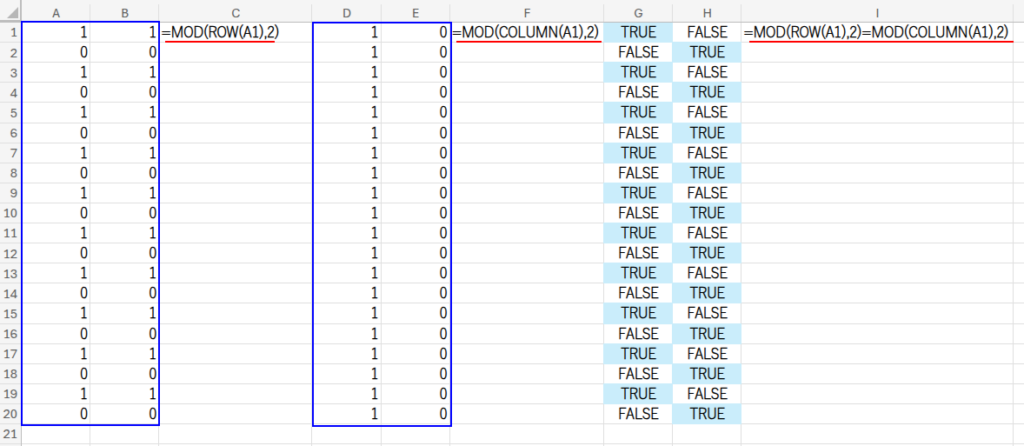
- A1セル：行(奇数)の余り1 = 列(奇数)の余り1 → TRUE
- B1セル：行(奇数)の余り1 ≠ 列(偶数)の余り0 → FALSE
- A2セル：行(偶数)の余り0 ≠ 列(奇数)の余り1 → FALSE
- B2セル：行(偶数)の余り0 = 列(偶数)の余り0 → TRUE
・IF(..., ROW(A1), ""): そして、IF関数が、判定結果がTRUEなら行番号そのものを、FALSEなら空白（””）を表示しているのです。見事なロジックですよね！
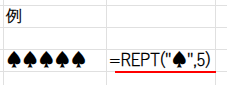
アプローチ2：REPT（もう一つの王道）
考えかた
ロジックは先ほどと全く同じですが、IF関数の代わりにREPT関数を使ってみましょう。
REPT関数は、通常は文字を繰り返すための関数ですが、ちょっとした裏ワザがあるのです。
数式と解説
A1セルに、以下の数式を入力し、同じくA1:B20の範囲にコピーします。
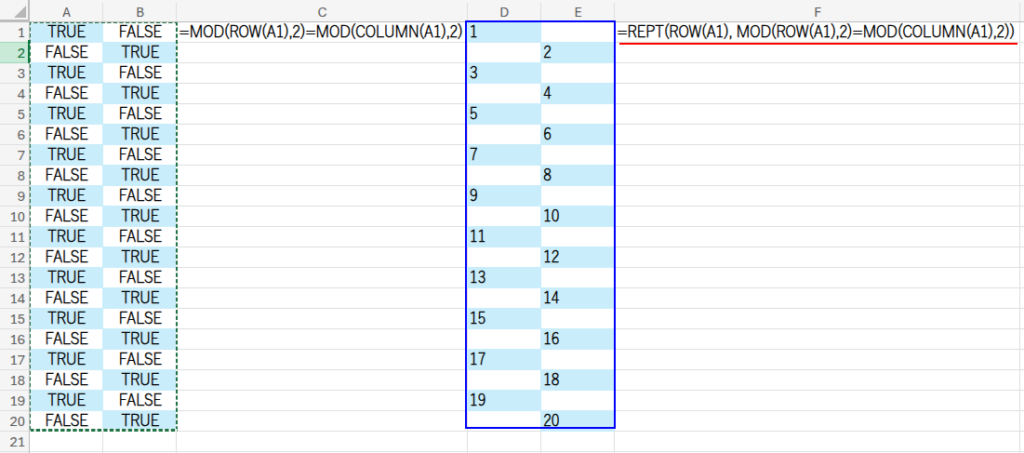
=REPT(ROW(A1), MOD(ROW(A1),2)=MOD(COLUMN(A1),2))
この数式、一体どうなっているのでしょうか？
・REPT(ROW(A1), ...): REPT関数は、REPT(繰り返したい文字, 回数) のように使います。今回は「行番号」を繰り返そうとしています。
・... MOD(...) = MOD(...): 第2引数の「回数」の部分には、アプローチ1と全く同じ論理式が入っています。
Excelでは、計算式の中で論理値を使うと、TRUEは「1」、FALSEは「0」として扱われます。
つまり、条件に合うセルでは「行番号を1回繰り返す（=行番号を表示する）」、
合わないセルでは「行番号を0回繰り返す（=何も表示しない）」という命令になり、
IF関数と全く同じ結果を生み出すのです。面白い使い方ですよね！
このままでは、数値が文字列として表示されているので、値に変換する必要がある場合は、以下のような数式にする必要があります。
=IFERROR(VALUE(REPT(ROW(A1), MOD(ROW(A1),2)=MOD(COLUMN(A1),2))),"")
VALUE関数で数値に変換しようとすると、残念ながら空白はエラーになります。
なので、IFERROR関数を使用してエラー処理をする必要があるのですが、今回はそこまで厳密に扱うつもりはないので、詳細は省略しますね。
Part 2：現代の魔法 – スピルで作るジグザグ
さて、ここからが本番です！
現代のExcelが誇る「スピル」機能と、強力な新関数たちを使って、たった一つの数式でこのジグザグ模様を一気に描き出します。
アプローチ3：IF + ISEVEN（シンプルなスピル配列）
A1セルに以下の数式を一つ入力するだけで、A1:B20の範囲に結果が自動で展開（スピル）されます。
=IF(ISEVEN(ROW(A1:A20)+COLUMN(A1:B1)),ROW(A1:A20),"")
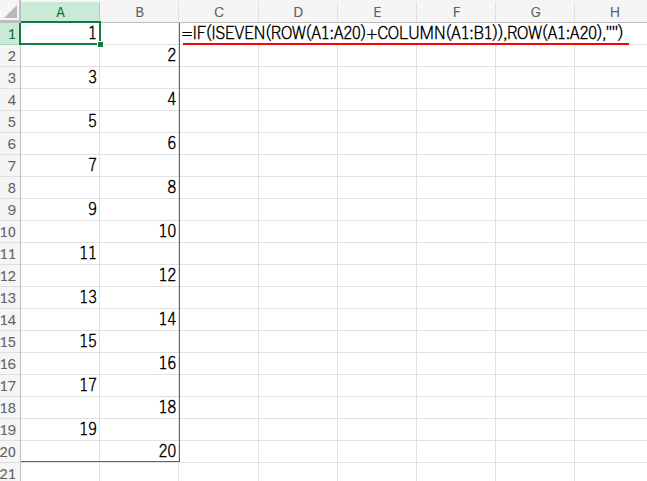
・ROW(A1:A20): まず、ROW関数が {1;2;3;...;20} という、20行1列の「縦配列」を作ります。
・COLUMN(A1:B1): 次に、COLUMN関数が {1,2} という、1行2列の「横配列」を作ります。
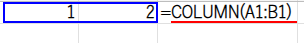
・... + ...: この「縦配列」と「横配列」を足し算すると、Excelは自動的に配列を拡張（ブロードキャスト）し、20行2列の巨大な足し算の表をメモリ上で作ります。
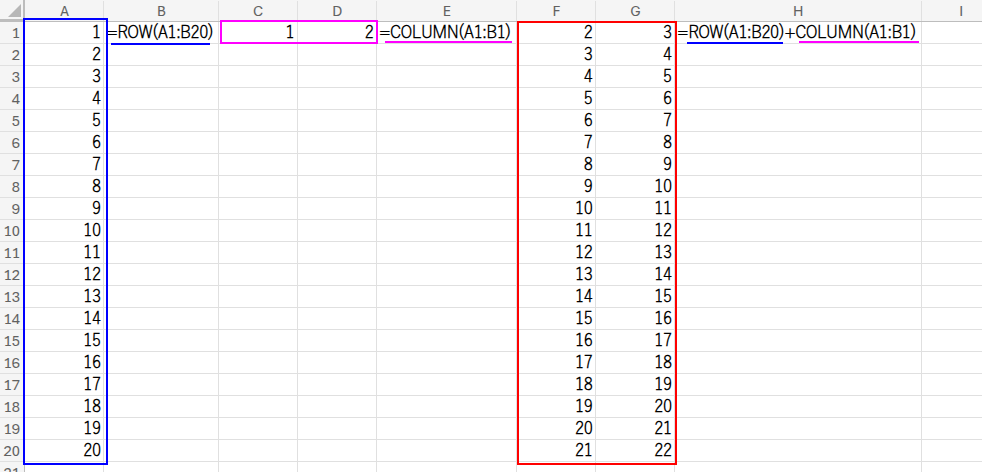
これを「動的配列」と呼びます。
・ISEVEN(...): その足し算の結果が偶数かどうかをISEVEN関数が判定し、{FALSE,TRUE;TRUE,FALSE;...}という市松模様のTRUE/FALSE配列を作ります。
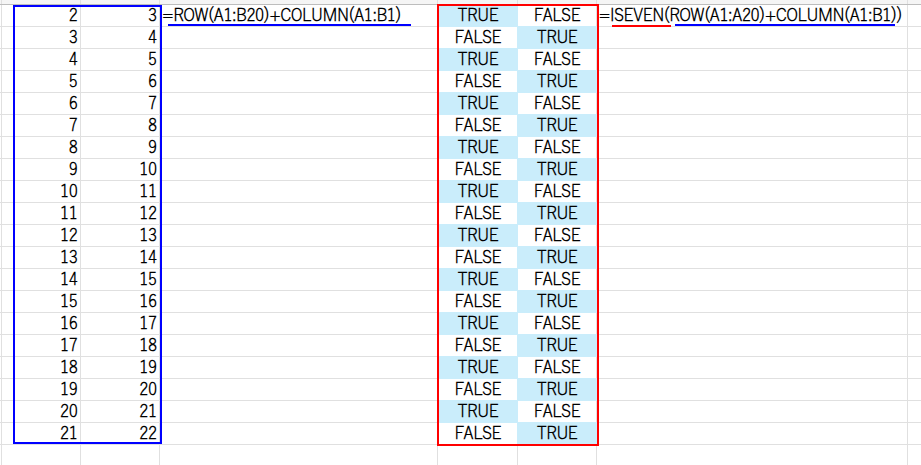
・IF(..., ROW(A1:A20), ""): 最後に、判定結果がTRUEの場所にだけ、ROW(A1:A20)が返す行番号の配列を表示させているのです。
アプローチ4：INDEX + TRANSPOSE（技巧派パズル）
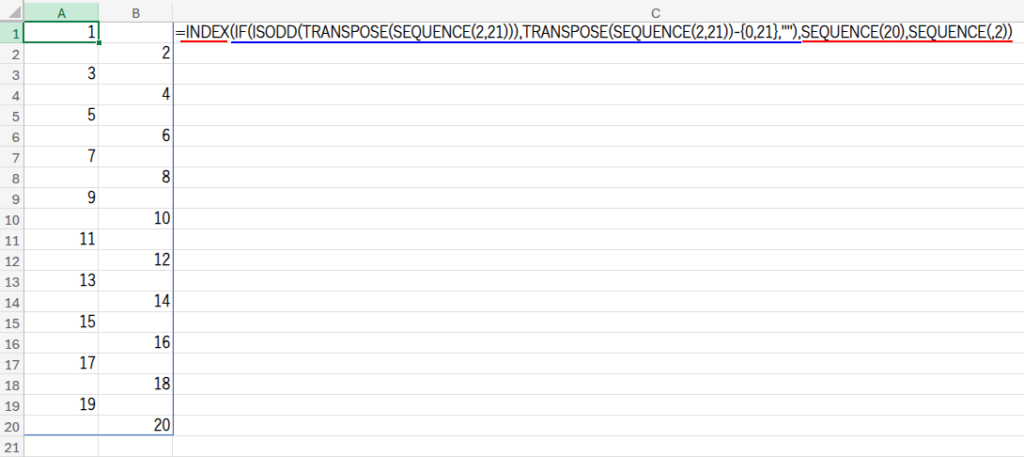
=INDEX(IF(ISODD(TRANSPOSE(SEQUENCE(2,21))),TRANSPOSE(SEQUENCE(2,21))-{0,21},""),SEQUENCE(20),SEQUENCE(,2))
これは非常に技巧的で、まるで頭の体操のような数式です。
・TRANSPOSE(SEQUENCE(2,21)): まず、SEQUENCE(2,21)で2行21列の連番配列を作り、それをTRANSPOSE関数で行と列を入れ替えて、21行2列の配列 {1,22; 2,23; ...} を生成します。
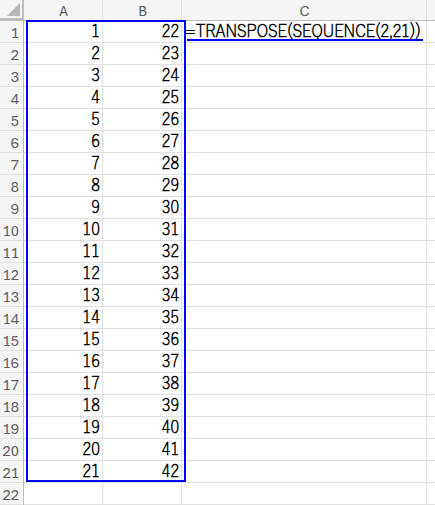
・IF(ISODD(...), ..., ""): 次に、この配列の数値が奇数かどうかを判定し、奇数だけを残します。結果は {1,""; "",23; 3,""; ...} という、歯抜けの配列になります。
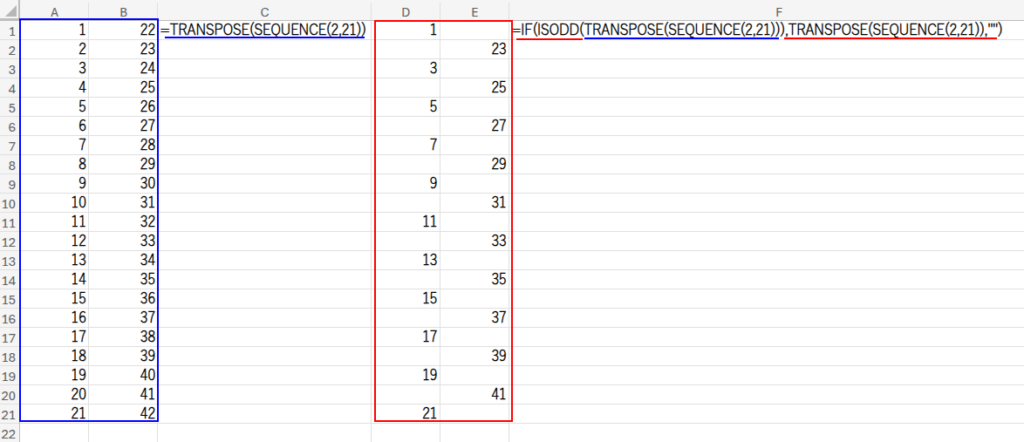
・...-{0,21}: ここが最大のトリック！この歯抜けの配列から、{0,21}という横配列を引き算します。
Excelは賢いので、1列目からは0を、2列目からは21を引いてくれます。結果、{1,""; "",2; 3,""; ...} という、ほぼ完成形のジグザグ配列が生まれるのです！
・INDEX(..., SEQUENCE(20), SEQUENCE(,2)): 最後に、INDEX関数が、この21行2列の配列から、必要な「20行2列」の部分だけを綺麗に抜き出して、完成です。
アプローチ5：CHOOSE（左右への振り分け）
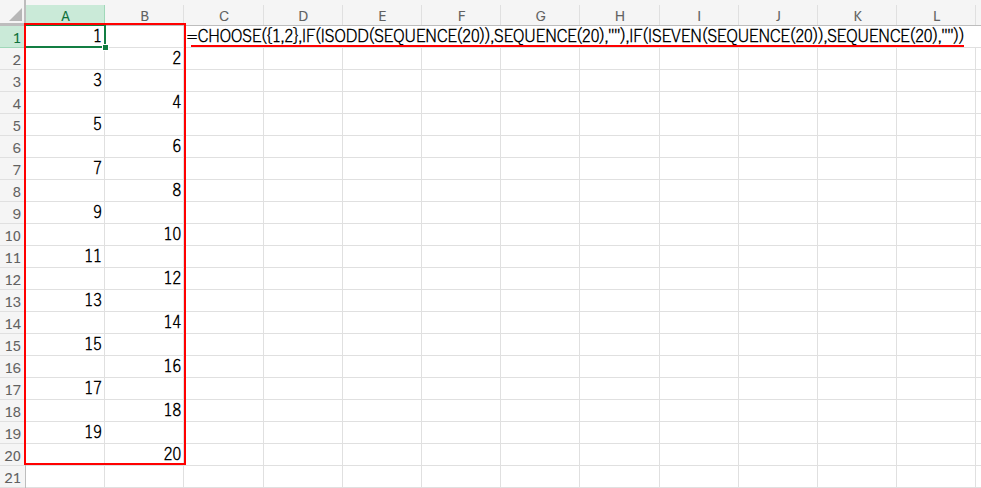
=CHOOSE({1,2},IF(ISODD(SEQUENCE(20)),SEQUENCE(20),""),IF(ISEVEN(SEQUENCE(20)),SEQUENCE(20),""))
この数式は、「左の列」と「右の列」を別々に作り、最後に合体させるという、非常に賢いアプローチです。
・IF(ISODD(SEQUENCE(20)),SEQUENCE(20),""): まず、SEQUENCE関数で1から20の連番を作り、ISODD関数で奇数行かどうかを判定します。
奇数行にだけ連番を配置した、1列目の配列 {1;"";3;"";...} が完成します。
・IF(ISEVEN(SEQUENCE(20)),SEQUENCE(20),""): 同じように、今度はISEVEN関数で偶数行かどうかを判定し、偶数行にだけ連番を配置した、2列目の配列 {"";2;"";4;...} を作ります。
・CHOOSE({1,2}, ...): そして、CHOOSE関数が、{1,2}という配列定数を使って、
「1番目の引数（奇数列）を1列目に、2番目の引数（偶数列）を2列目に配置しなさい」
と命令し、2つの配列を合体させて2列のジグザグ配列を生成します。
これは、配列を結合するための伝統的なテクニックの一つです。
アプローチ6：HSTACK（最新・最強の合体術）
=HSTACK(IF(MOD(SEQUENCE(20),2)=1,SEQUENCE(20),""),IF(MOD(SEQUENCE(20),2)=0,SEQUENCE(20),""))
アプローチ5のCHOOSEを使った方法は少しトリッキーでしたよね？
そこで登場するのが、最新関数HSTACKです！
【HSTACK関数の使い方】
HSTACK関数は、複数の配列を「水平方向（Horizontally）」にガチャンと連結する、非常にシンプルで強力な関数です。=HSTACK(配列1, 配列2, ...) のように使います。
この数式は、アプローチ5と全く同じように「奇数だけの列」と「偶数だけの列」を別々に作り、最後にそれをHSTACKで横に連結しているだけ。
CHOOSEよりもずっと直感的で分かりやすいですね！
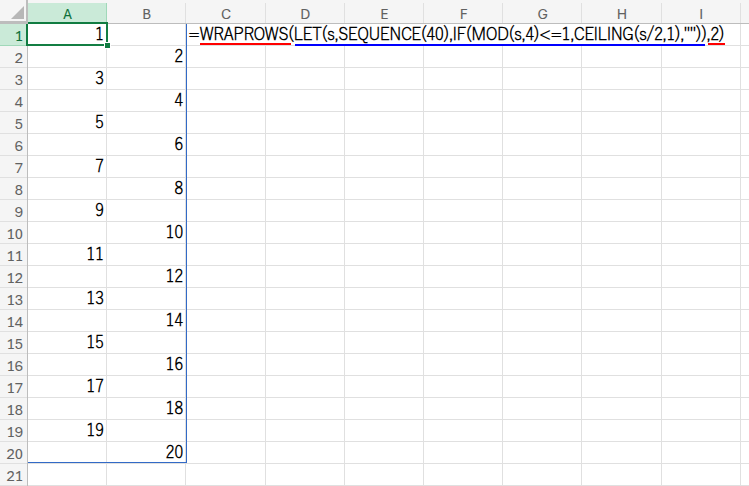
アプローチ7：WRAPROWS（1次元からの再構築）
=WRAPROWS(LET(s,SEQUENCE(40),IF(MOD(s,4)<=1,CEILING(s/2,1),"")),2)
これは、また全く違う角度からのアプローチです。
【WRAPROWS関数の使い方】
WRAPROWS関数は、1列（または1行）の長い配列を、指定した数で「折り返して（Wrap）」複数行の配列に変換する関数です。=WRAPROWS(1次元配列, 折り返す数) のように使います。
この数式は、まずLET関数を使って、{1;"";"";2;3;"";"";4;...} のような、40個の要素を持つ「1次元の長い配列」を作り出します。（この配列を作るロジック自体も非常に巧妙です！）
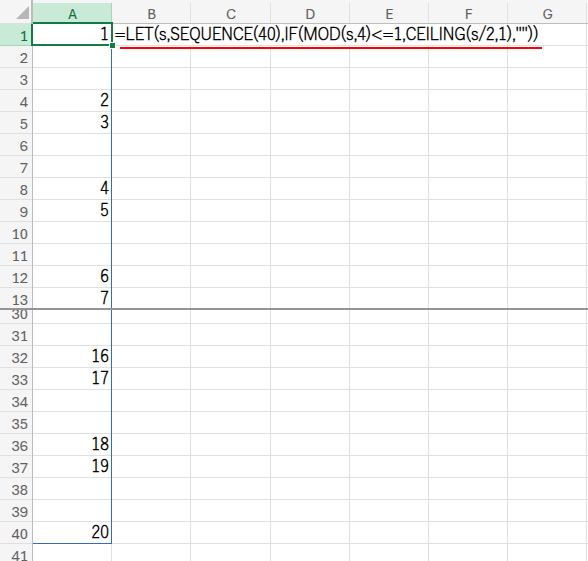
そして、最後にWRAPROWS関数が、この長い配列を「2個ずつ」折り返していくことで、目的の20行2列のジグザグ配列を再構築しているのです。
まさにパズルですよね！
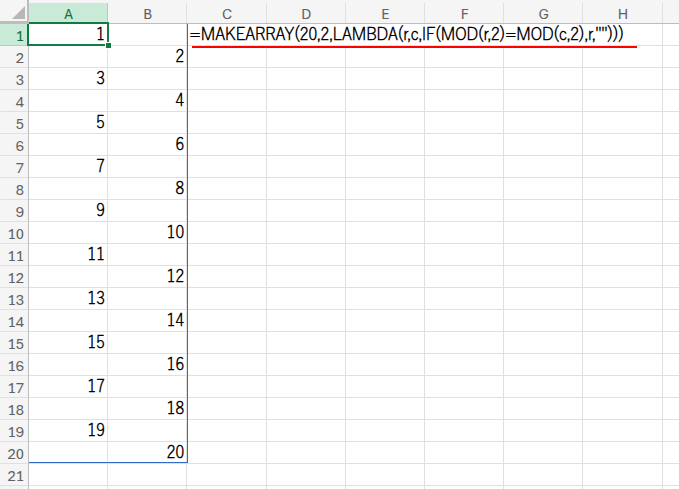
アプローチ8：MAKEARRAY + LAMBDA（無からの創造）
=MAKEARRAY(20,2,LAMBDA(r,c,IF(MOD(r,2)=MOD(c,2),r,"")))
ここからは、Excelの新次元を切り開くLAMBDA（ラムダ）関数の登場です！
【LAMBDAとMAKEARRAYの使い方】
LAMBDAは、自分だけのオリジナル関数を作る機能です。
そして、MAKEARRAYは、MAKEARRAY(行数, 列数, LAMBDA(r, c, 計算式)) のように使い、指定したサイズの配列を、LAMBDAで作った計算ルールに従ってゼロから生成する、まさに「創造主」のような関数です。
「r」は行番号、「c」は列番号を意味します。
この数式は、「20行2列の配列を作る。各セルの値は、IF(MOD(r, 2) = MOD(c, 2), r, "")というルールで決めなさい」と命令しています。
お気づきですか？この計算ルール、アプローチ1で使ったものと全く同じですよね！
MAKEARRAYは、フィルコピーが必要だった古典的なロジックを、スピル機能の世界に昇華させてくれる、非常にエレガントな関数なのです。
アプローチ9：REDUCE + LAMBDA（積み上げの美学）
=DROP(REDUCE(HSTACK("",""),SEQUENCE(20),LAMBDA(a,b,VSTACK(a,IF(MOD(b,2)=1,HSTACK(b,""),HSTACK("",b))))),1)
さあ、最後は最も難解で、しかし最も強力な方法の一つ、REDUCE関数です！
【REDUCE関数の使い方】
REDUCEは、REDUCE(初期値, 配列, LAMBDA(a, b, 計算式)) のように使います。
配列の各要素を順番に取り出し（b）、前のステップまでの計算結果（a）と合わせて、新しい計算結果を「蓄積（Accumulate）」していく、まるでループ処理のような関数です。
この数式は、
1. 空っぽの2列の配列からスタートし（HSTACK("","")）、
2. 1から20までの数字（SEQUENCE(20)）を一つずつ取り出し、
3. その数字が奇数なら {数字, ""}、偶数なら {"", 数字} という新しい行を作り、
4. 前のステップまでに積み上げた配列の下に、新しい行をどんどん追加（VSTACK）していく…
という処理を20回繰り返しています。
最後に、DROP関数で、最初の不要な空っぽの行を削除して完成です。
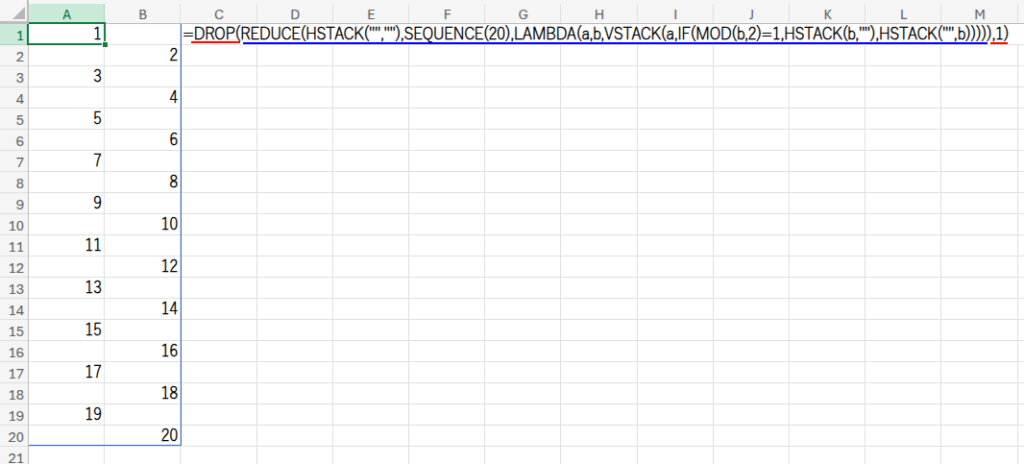
一行一行、配列を組み立てていく様子は、まさに職人技ですね！
まとめ：同じゴール、無限のアプローチ
たった一つのシンプルなゴールに対して、これほどまでに多様なアプローチが存在することに、驚かれたのではないでしょうか。
古いけれど堅実なロジック、最新関数を使ったエレガントな解決策、そして一見難解でも強力なループ処理まで。
どの数式が優れている、というわけではありません。それぞれの数式に、それぞれの美学と歴史があります。
今回の関数パズルが、皆さんの「数式の引き出し」を増やし、Excelの持つ無限の可能性を感じるきっかけになれば、これほど嬉しいことはありません。
今回登場した関数リスト
比較的古い関数
- IF(論理式, 値が真の場合, [値が偽の場合]): 条件を判定し、処理を分岐させます。
- ROW([参照]): セルの行番号を返します。参照を範囲にすると、行番号の配列になります。
- COLUMN([参照]): セルの列番号を返します。参照を範囲にすると、列番号の配列になります。
- MOD(数値, 除数): 割り算の「余り」を返します。周期的な計算が得意です。
- REPT(文字列, 繰り返し回数): 指定した文字列を、指定した回数だけ繰り返します。
- ISEVEN(数値): 数値が偶数ならTRUEを返します。
- ISODD(数値): 数値が奇数ならTRUEを返します。
- SEQUENCE(行, [列], [開始], [ステップ]): 連続した数値の配列を生成します。
- INDEX(配列, 行番号, [列番号]): 配列の中から、指定した行と列の位置にある値を取り出します。
- TRANSPOSE(配列): 配列の行と列を入れ替えます。
- CHOOSE(インデックス, 値1, [値2], …): インデックス番号に基づいて、リストから値を選択します。配列操作にも使えます。
新しい関数
- HSTACK(配列1, [配列2], …): 複数の配列を水平方向（横）に連結します。
- VSTACK(配列1, [配列2], …): 複数の配列を垂直方向（縦）に連結します。
- WRAPROWS(ベクトル, 折り返す数, [空白処理]): 1次元の配列を指定した数で折り返し、2次元の配列に変換します。
- LET(名前1, 値1, [名前2, 値2…], 計算): 数式内で計算結果や値に名前をつけ、可読性を高めます。
- MAKEARRAY(行数, 列数, LAMBDA): LAMBDAで定義したルールに従って、指定したサイズの配列を生成します。
- REDUCE(初期値, 配列, LAMBDA): 配列の各要素を順番に処理し、結果を蓄積していきます。
- DROP(配列, 行数, [列数]): 配列の先頭または末尾から、指定した数の行または列を削除します。
- LAMBDA(引数, 計算式): オリジナルのカスタム関数を作成する機能。他の関数と組み合わせて使います。
