- はじめに:その桁数、LEN関数以外で数えられますか?
- 準備:挑戦者とルールを決める
- 11のアプローチで、「桁数」を完全攻略!
- まとめ:回り道こそ、最大の近道だ!
はじめに:その桁数、LEN関数以外で数えられますか?
「数値の桁数を数えたい?そんなの、LEN関数で一発でしょ?」
そう思ったあなた、大正解!
ほとんどの場合、LEN関数が最も簡単で分かりやすい方法です。
でも、ちょっと待ってください!
Excelの世界は、私たちが思っているよりもずっと奥深いのです。
もし、その便利なLEN関数が、今日から使用禁止になったとしたら?
もし、「文字列として数える」のではなく、「純粋な数値計算」だけで桁数を求めなければならないとしたら?
「え、そんなことできるの?一体どうやって…?」
そんな、実務では絶対に使わないけれど、関数好きの心をくすぐる「無駄な桁数カウント」に、挑戦してみたいと思います!
今回の冒険では、あえて便利な新関数は封印!
Excel 2019以前、いえ、もっと古いバージョンでも使えるような、基本的な(レガシーな)関数だけで、11種類ものアプローチでこの問題に挑みます。
目的は、
数学的な考え方が、どのようにExcelの数式ロジックに変わるのか、その本質を深く理解すること!
この関数パズルを通して、あなたのExcel関数への理解が、さらに深まるかもしれませんよ!
本記事では、無料のWeb版Excelを使用して検証および画像の作成を行っています。Windowsはもちろん、MacやLinuxの方もブラウザさえあれば挑戦できます!
準備:挑戦者とルールを決める
何事も、まずは準備から。まっさらなシートを用意してください。
A1セルに、今回の挑戦者となる、好きな整数を入力します。
今回は、分かりやすく10桁の「9876543210」を入力してみましょう。
ゴールは、この数値の桁数である「10」を、これから紹介する11個の異なる数式で導き出すことです。
【今回のルール】
1. 対象は1以上の正の整数のみ! 小数や負の数は考えず、純粋なロジックを楽しみます。
2. 15桁まで扱えればOK! なぜ15桁なのか?これは、Excelが内部的に数値を「倍精度浮動小数点数」という形式で保持しており、その有効桁数が約15桁であるためです。それより大きい数値は、下の桁が丸められてしまう可能性があるのです。Excelの歴史的な仕様ですね。
11のアプローチで、「桁数」を完全攻略!
関数の詳細な仕様については、Microsoft公式のヘルプも参考にしてください。
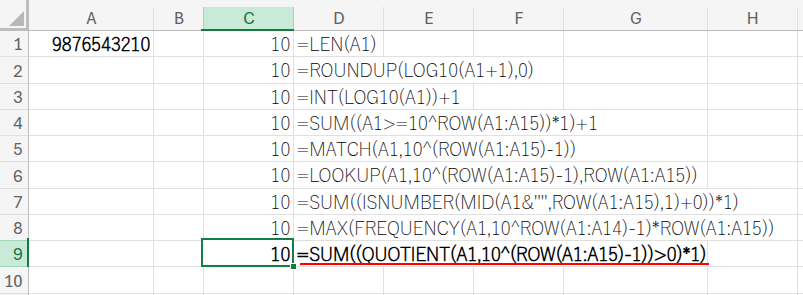
準備は整いました!C列に、様々な数式を入力して、A1セルの桁数を計算していきましょう!
アプローチ1:LEN – 王道にして最強
考えかた
まずは、誰もが最初に思い浮かべる王道です。
数値を文字列として扱い、その「文字数」を数えることで、桁数とします。
数式と解説
=LEN(A1)
LEN関数は、セルに入力された値の文字数を返します。
数値を引数にすると、Excelが自動的にそれを文字列として解釈してくれるため、一発で答えが出ます。シンプルイズベストですね。

アプローチ2:ROUNDUP + LOG10 – 対数の力
考えかた
ここからは、純粋な数値計算の世界です。
数学好きなら、「桁数」と聞いて「対数(Logarithm)」を思い浮かべるかもしれません。
常用対数(LOG10)は、その数値が「10の何乗か」を示します。
例えば、LOG10(100)は2、LOG10(1000)は3です。
この性質を使えば、桁数が分かりそうですよね?
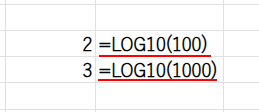
数式と解説
=ROUNDUP(LOG10(A1+1),0)
・A1+1: なぜ1を足すのでしょうか?
もし、A1が「100」の場合、LOG10(100)はちょうど「2」になってしまいます。
これを切り上げても答えは「2」桁となり、間違いです。
そこで、あらかじめ1を足して「101」にしておくことで、LOG10(101)が「2.004…」となり、正しく3桁と計算できるようにする、巧妙なテクニックです。

LOG10(...): 常用対数を計算します。ROUNDUP(...,0): 計算結果を、小数点以下を切り上げて整数にします。
アプローチ3:INT + LOG10 – 切り捨ての発想
考えかた
切り上げがあるなら、切り捨てでもできるはず!
対数の「整数部分」は、「桁数 – 1」と常に一致するという性質を利用します。
数式と解説
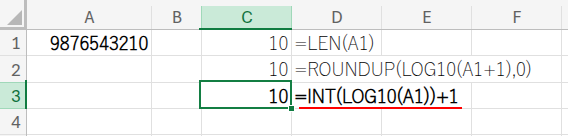
=INT(LOG10(A1))+1
・LOG10(A1): 例えば、A1が「987」なら、LOG10(987)は約「2.99…」です。
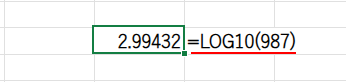
・INT(...): この結果の整数部分だけを取り出すと、「2」になります。これは「桁数 – 1」ですね。
・... + 1: 最後に、1を足すことで、正しい桁数「3」を導き出します。アプローチ2より、少しだけシンプルですね!

アプローチ4:SUM + ROW + 配列 – 比較の積み重ね
考えかた
ここからは配列計算の世界です。
「10のn乗(10, 100, 1000…)」のリストを作り、入力された数値が、そのリストの何番目の値まで「以上」であるかを数える、という考え方です。
数式と解説
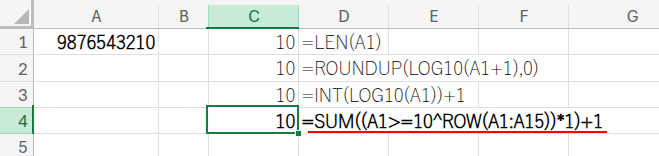
=SUM((A1>=10^ROW(A1:A15))*1)+1
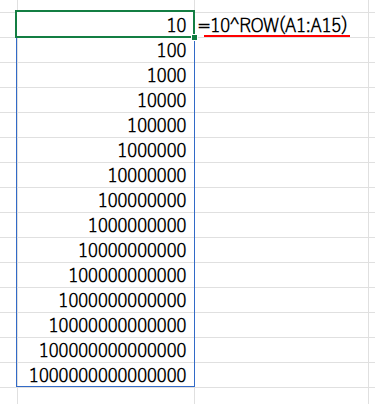
・10^ROW(A1:A15): ROW(A1:A15)で{1;2;…;15}という配列を作り、10^...で{10;100;…;10の15乗}という「10のn乗リスト」を生成します。
・A1 >= ...: 入力値が、このリストの各値以上かどうかを判定し、TRUE/FALSEの配列を作ります。
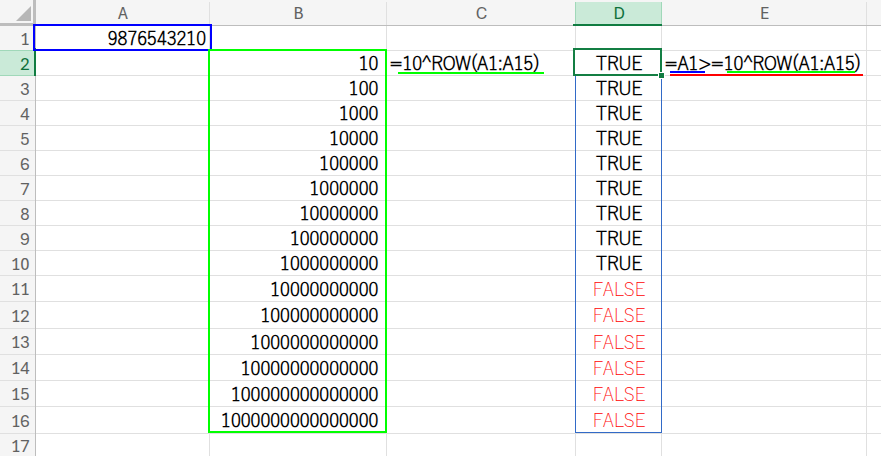
・... * 1: TRUEを1、FALSEを0に変換します。

・SUM(...)+1: TRUEの個数を合計し、最後に1を足すことで桁数を計算します。
(1桁の場合を考慮して最後に+1しています)
アプローチ5:MATCH – 近似一致の美学
考えかた
アプローチ4と同じ「10のn乗リスト」を使いますが、今度はMATCH関数の「近似一致」で、一発で位置を特定します。非常に美しい数式です。
数式と解説
=MATCH(A1,10^(ROW(A1:A15)-1))
・10^(ROW(A1:A15)-1): {1;10;100;…}という、1から始まる「10のn乗リスト」を作ります。
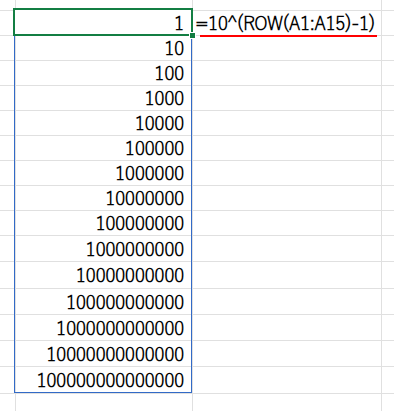
・MATCH(A1, ...): 第3引数を省略したMATCH関数は、「検索値以下の、最も大きい値」がリストの何番目にあるかを探します。
例えばA1が「987」なら、リストの中で987以下で最も大きいのは「100」ですね。
つまり、その「100」はリストの3番目にあるので、MATCHは「3」を返します。これがそのまま桁数になるわけです!
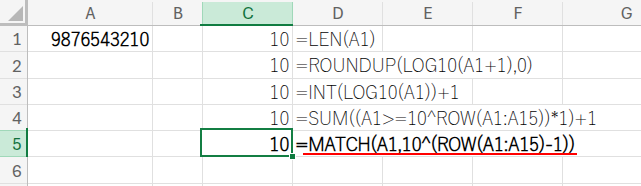
アプローチ6:LOOKUP – 近似一致の元祖
考えかた
MATCH関数と似た動きをする、近似一致の元祖LOOKUP関数でも同じことができます。
LOOKUP関数については以下の記事でも紹介しています。
数式と解説
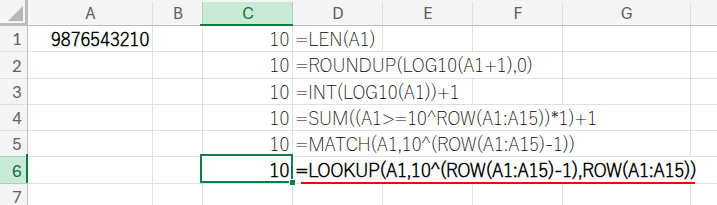
=LOOKUP(A1,10^(ROW(A1:A15)-1),ROW(A1:A15))
・LOOKUP(A1, 10^..., ROW(...)): LOOKUP関数も、検索値「987」以下の最大値「100」を検索範囲から見つけ出します。
そして、それに対応する「戻り範囲」(今回はROW(A1:A15)、つまり{1;2;…;15})から、同じ位置にある値「3」を返してくれます。
アプローチ7:MID + ISNUMBER – 文字列からの逆襲
考えかた
一度数値を文字列に変え、MID関数で1文字ずつに分解し、それが再び数値に戻せるかどうかを判定して、文字(数字)の個数を数えるという、少し回りくどいけれど確実な方法です。
数式と解説
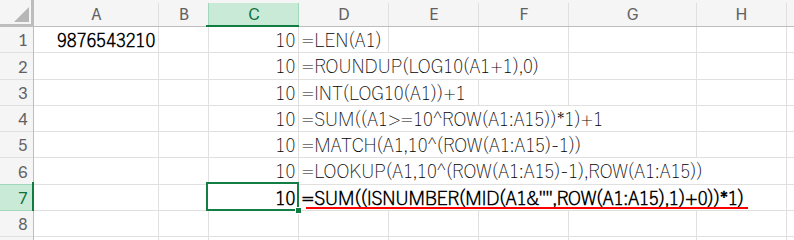
=SUM((ISNUMBER(MID(A1&"",ROW(A1:A15),1)+0))*1)
・A1&"": まず、数値に空文字を連結して、強制的に文字列に変換します。

・MID(...,ROW(A1:A15),1): 1文字目から15文字目までを、1文字ずつ順番に抜き出し、文字の配列を作ります。
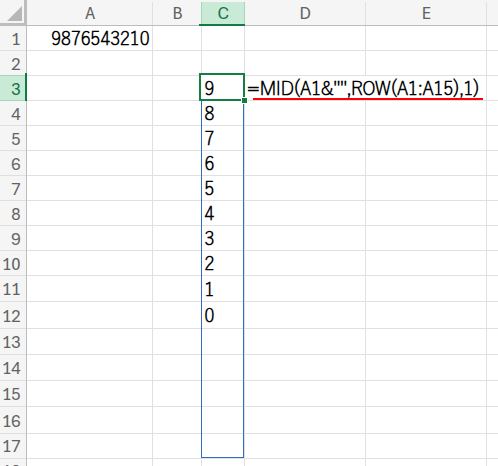
・...+0: 抜き出した各文字に0を足してみます。元の文字が数字なら計算できますが、文字が存在しない部分(空白)はエラーになります。
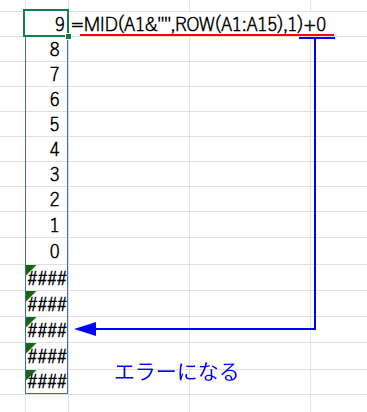
・ISNUMBER(...): 0を足した結果が、数値として成立するかどうかを判定します。数字だった部分はTRUE、エラーになった部分はFALSEになります。
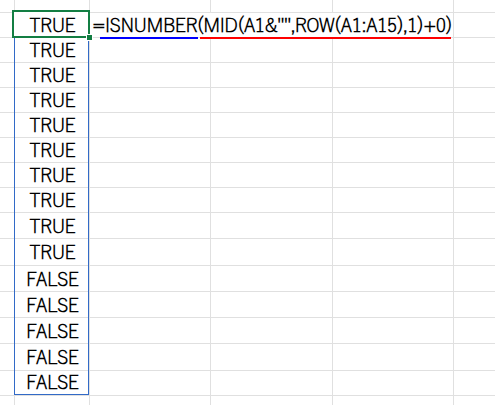
・SUM(...*1): TRUE(1)の個数を合計することで、桁数を数えます。
アプローチ8:FREQUENCY – 統計関数の逆襲
考えかた
今度は、統計関数であるFREQUENCYを使った、超絶マニアックな方法です。
数値がどの階級(9以下、99以下、999以下…)に属するかを判定し、その位置から桁数を導き出します。
FREQUENCY関数については以下の記事で詳しく解説しています。
数式と解説
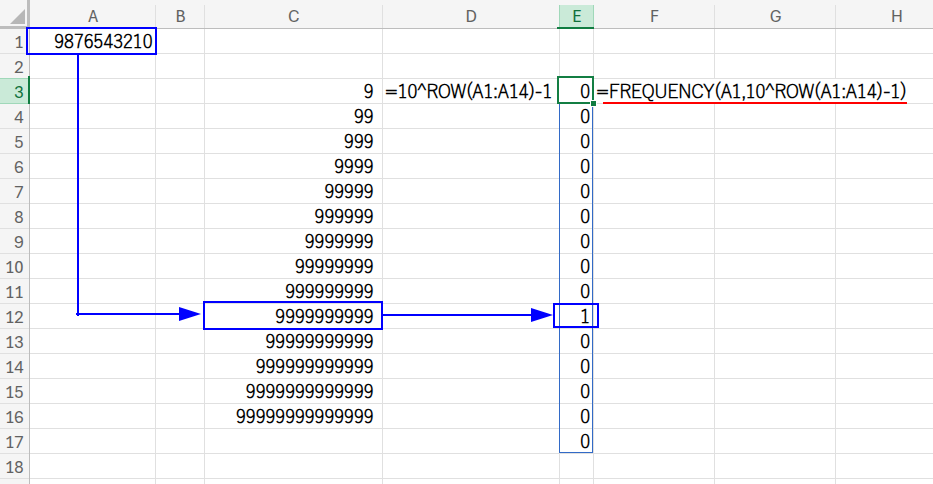
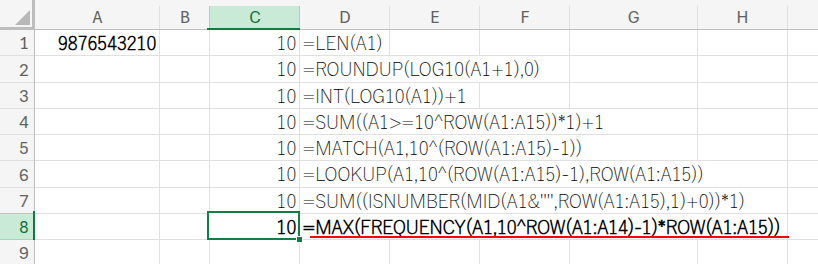
=MAX(FREQUENCY(A1,10^ROW(A1:A14)-1)*ROW(A1:A15))
・10^ROW(A1:A14)-1: {9;99;999;…}という、「区間」の上限値の配列を作ります。
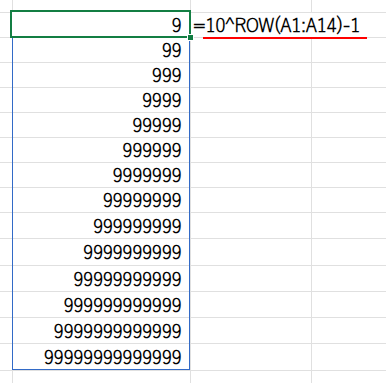
・FREQUENCY(A1, ...): FREQUENCY関数が、A1の数値がどの区間に属するかを判定し、該当する場所だけが「1」になる配列(例: {0;0;1;0…})を返します。
・...*ROW(A1:A15): この配列に、行番号の配列{1;2;3…}を掛け合わせ、該当する桁数だけが残った配列(例: {0;0;3;0…})を作ります。
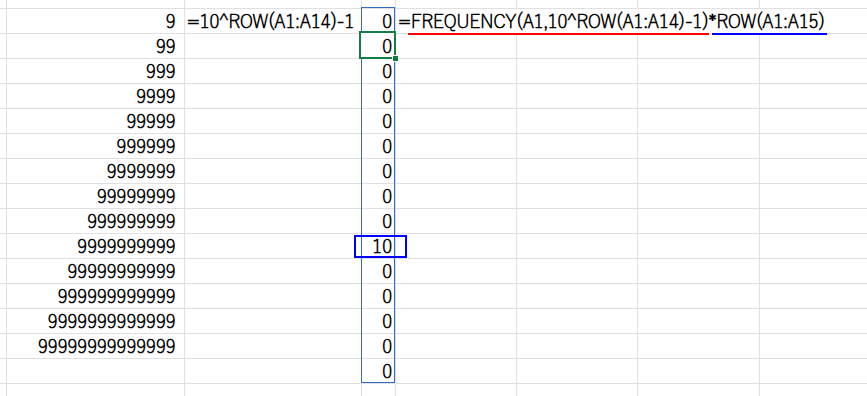
・MAX(...): 最後に、その配列の最大値を取れば、それが桁数になります。
アプローチ9:QUOTIENT – 商が0になるまで
考えかた
数値を1, 10, 100…と順番に割っていき、その「商(整数部分)」が0より大きい間は、まだ桁が存在すると考えられます。この商が0になる直前までを数える、というロジックです。
数式と解説
=SUM((QUOTIENT(A1,10^(ROW(A1:A15)-1))>0)*1)
・10^(ROW(A1:A15)-1): {1;10;100;…}という、割る数のリストを作ります。
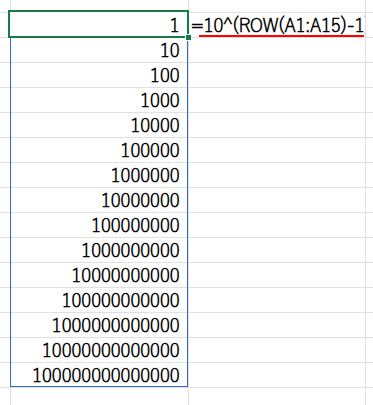
・QUOTIENT(A1, ...): A1をリストの各値で割り、その商の整数部分の配列を求めます。
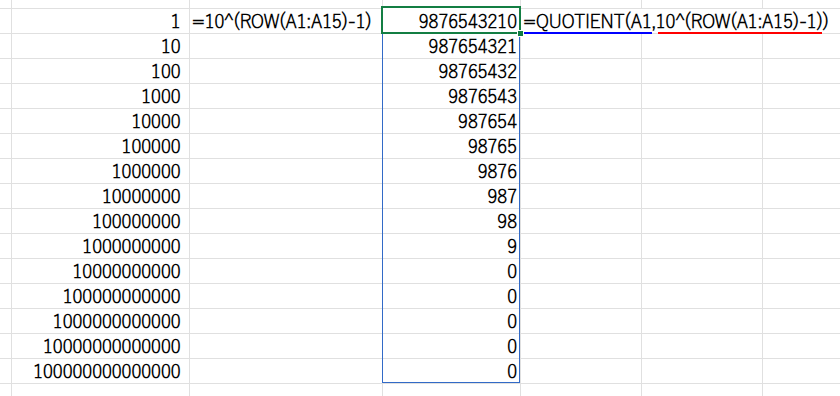
・... > 0: 商が0より大きいかどうかを判定し、TRUE/FALSEの配列を作ります。
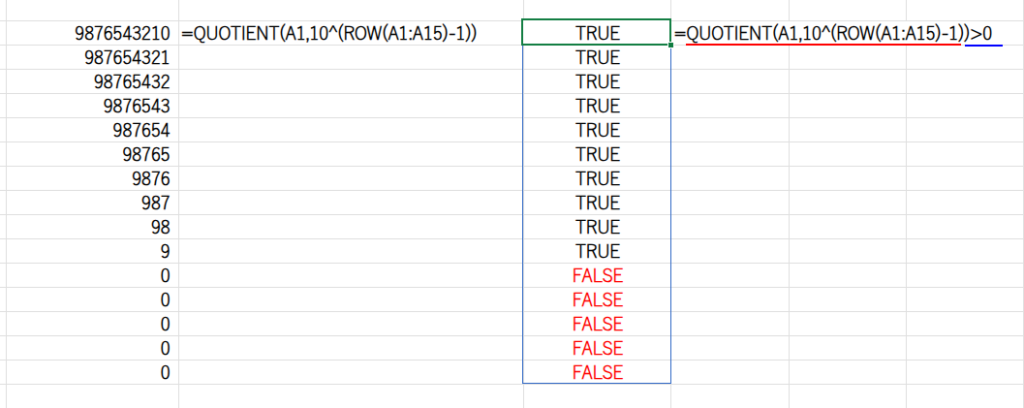
・SUM(...*1): TRUE(1)の個数を合計すれば、それが桁数になります。
アプローチ10:COUNT – エラーを味方につける
考えかた
これは、エラーを意図的に発生させて、それを逆手に取る方法です。
COUNT関数は、数値だけを数え、エラー値は無視するという性質を利用します。
数式と解説
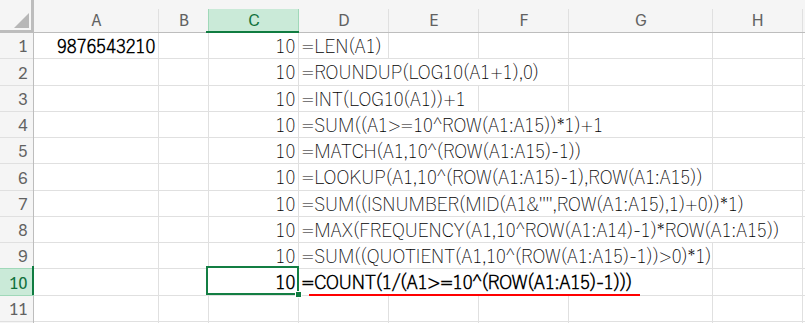
=COUNT(1/(A1>=10^(ROW(A1:A15)-1)))
・A1>=10^(ROW(A1:A15)-1): {TRUE;TRUE;…;FALSE;…}という、おなじみの条件配列を作ります。
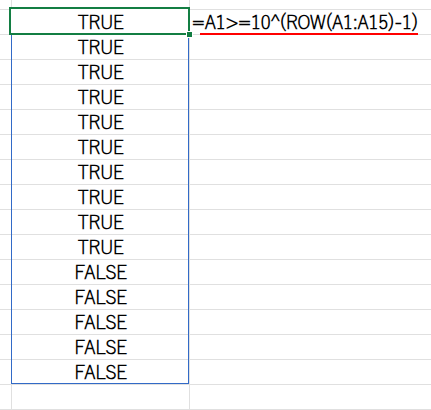
・1/...: この配列で1を割ります。1/TRUEは「1」、1/FALSEはエラー「#DIV/0!」になります。
結果、{1;1;...;#DIV/0!;...}という、数値とエラーが混在した配列が生まれます。
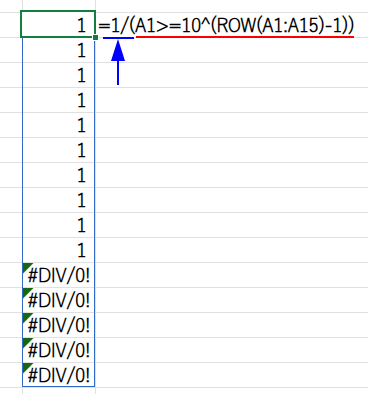
・COUNT(...): COUNT関数が、この配列の中から数値(1)の個数だけを数え、エラーは無視します。結果として、桁数が求められるのです!
アプローチ11:IF – 究極の原始的手法
考えかた
最後は、関数パズルというよりは、もはや根性の世界です。
IF関数をひたすらネスト(入れ子に)して、15桁まで順番に条件分岐していきます。
数式と解説
=IF(A1>=100000000000000,15,IF(A1>=10000000000000,14,IF(...,IF(A1>=10,2,IF(A1>=1,1,0))...))) ※下の画像を参照ください
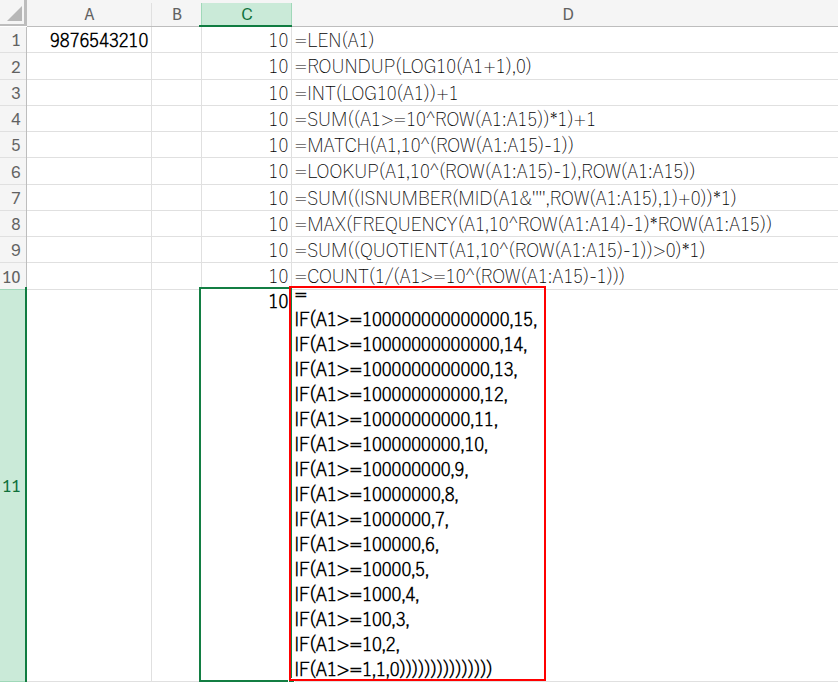
「もし10の14乗以上なら15桁、そうでなければ、もし10の13乗以上なら14桁、そうでなければ…」という条件分岐を、15回繰り返しています。
美しさはありませんが、四の五の言わずに力でねじ伏せる、という潔さがありますね(笑)。
まとめ:回り道こそ、最大の近道だ!
たった一つのシンプルなゴールに対して、これほどまでに多様なアプローチが存在することに、驚かれたのではないでしょうか。
実務で使うなら、アプローチ1のLENが最も手軽かもしれません。(整数であれば…)
しかし、LOG10を使った数学的な解法や、配列計算を駆使した様々なパズルは、Excel関数の本当の力と、その背景にある数学的な美しさを教えてくれます。
また、12345.123のような小数値に対しても正しく機能します。
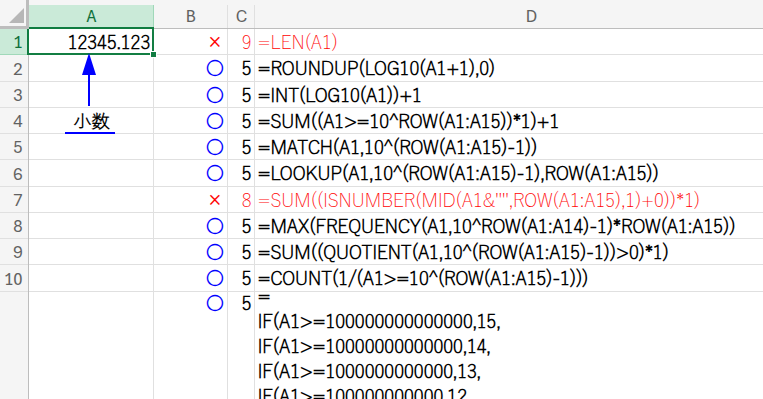
一見、無駄に見える「回り道」こそが、実は関数の本質的な理解へとつながる、最大の近道なのかもしれません。
今回の関数パズルが、皆さんのExcelへの知的好奇心をさらに深めるきっかけになれば、これほど嬉しいことはありません。