はじめに:合計といえばSUM関数!…本当にそれだけ?
「Excelで合計を出すなら、SUM関数でしょ?」
そう思ったあなた、大正解!
ほとんどの場合、SUM関数が最も簡単で分かりやすい方法です。
でも、ちょっと待ってください!
好評だった「合計はSUM以外でもできる!意外な関数で合計を出す5つの方法」の冒険、その続編へようこそ!
前回、SUM関数を使わずに合計を求める5つの方法を探求しましたが、Excelの世界は、私たちが思っているよりも、もっともっと奥深いのです。
「え、まだ他にも方法があるの?しかも、もっとマニアックな方法が?」
その通り!今回の【第2弾】では、前回紹介しきれなかった、さらに奇妙で、美しく、そして無駄な(褒め言葉です!)合計計算の数式たちを、8つのカテゴリに分けて、たっぷりとご紹介します!
財務関数、複素数関数、行列計算…普段の業務では決して出会うことのない、強力な関数たちが、この「合計」というシンプルな目的のために、驚くべき姿を見せてくれますよ。
厳密には「合計」とは言えないような数式もあります。(ただの足し算!といいたくなるものも。)そこは、Excelで暇つぶしということで、どうか大目に見てください。
もちろん、今回紹介する数式はほんの一例です。
Excelの世界は広大なので、この記事をきっかけに、あなただけのオリジナル合計数式を探してみるのも一興ですよ!
この関数パズルを通して、あなたの「関数の引き出し」をさらに増やし、Excelの持つ無限の可能性を一緒に楽しんでいきましょう!
準備:今回の挑戦者
本記事では、無料のWeb版Excelを使用して検証および画像の作成を行っています。Windowsはもちろん、MacやLinuxの方もブラウザさえあれば挑戦できます!
何事も、まずは準備から。まっさらなシートのA1セルを起点に、3行2列のシンプルな数値の表を用意しましょう。
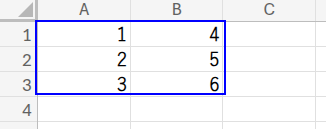
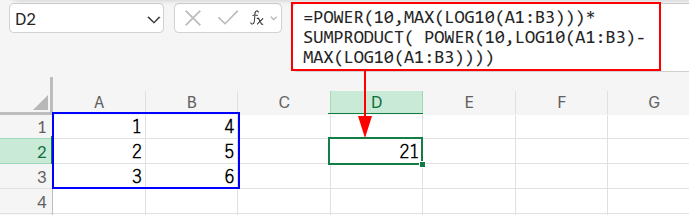
私たちのゴールは、このA1:B3の範囲に含まれるすべての数値の合計「21」を、これから紹介する様々な数式で導き出すことです。
8つのジャンルで挑む、合計計算の冒険!
関数の詳細な仕様については、Microsoft公式のヘルプも参考にしてください。
1. 王道 – これぞ基本の「き」
考えかた
まずは肩慣らし。SUM関数の基本的な使い方を再確認しておきましょう。
数式と解説
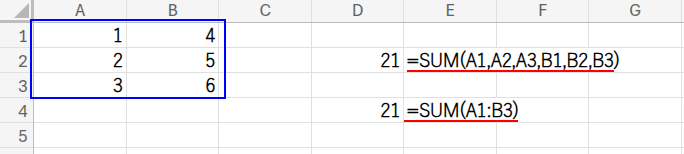
=SUM(A1,A2,A3,B1,B2,B3)
このように、引数に合計したいセルを一つひとつカンマで区切って指定する方法と、
=SUM(A1:B3)
このように、合計したい範囲(配列)をまとめて指定する方法があります。どちらも結果は同じ「21」ですね。言うまでもありません!
2. 集計系 – SUMの頼れる仲間たち
考えかた
SUMと名前は似ていなくても、合計ができる関数は他にもあります。集計のプロフェッショナルたちにご登場願いましょう。
数式と解説
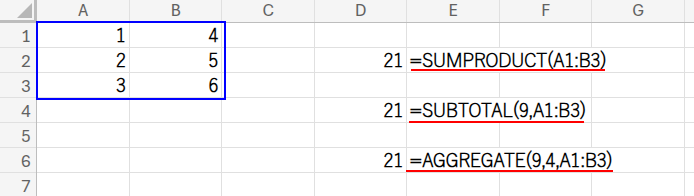
=SUMPRODUCT(A1:B3)
SUMPRODUCT関数は、本来は複数の配列の同じ位置にある要素同士を掛け算し、その結果を合計する関数ですが、引数が一つだけだと、単純にその配列の合計を返してくれます。

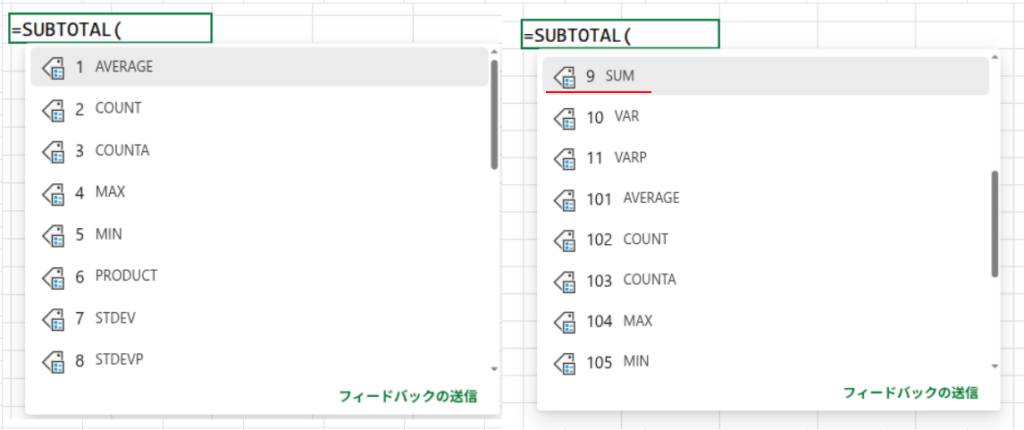
=SUBTOTAL(9,A1:B3)
SUBTOTAL関数は、集計の万能選手。第1引数の「集計方法」に「9」を指定すると、「合計」を意味します。
この関数の真価は、フィルターで非表示になっている行を無視して集計できる点にあります。
=AGGREGATE(9,4,A1:B3)
AGGREGATE関数は、SUBTOTALをさらに強化したような関数。第1引数の「9」は同じく「合計」。

第2引数の「オプション」で、非表示行だけでなく、エラー値なども無視する設定が可能です。(今回は「4」でエラー値を無視する設定にしていますが、省略しても動作します)
3. 他のSUM系 – ちょっと変わった親戚たち
考えかた
名前に「SUM」と付く関数の中にも、一風変わった方法で合計を計算できる、個性的な面々がいます。
数式と解説
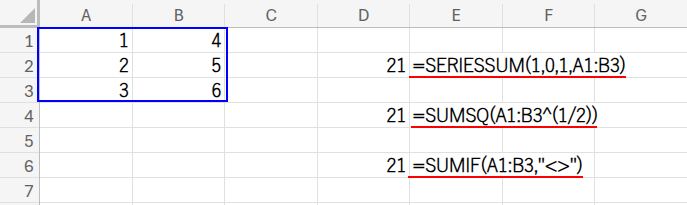
=SERIESSUM(1,0,1,A1:B3)
出ました!実務で一生使うことがない関数ランキング、堂々の第1位(筆者調べ)、SERIESSUM関数です!
これは本来、べき級数(a*x^n + b*x^(n+m) + …)を計算するための、非常に数学的な関数。

しかし、引数xを「1」、初項nを「0」、増分mを「1」にすると、なんと数式の各項が係数*1となり、単純な係数(A1:B3の値)の合計になるのです!まさに奇跡の呪文。
=SUMSQ(A1:B3^(1/2))
SUMSQ関数は、各数値を「2乗」して合計する関数。
それを逆手に取り、あらかじめ各数値を「1/2乗」(つまり平方根)しておきます。
それをSUMSQが2乗し直すことで、結果的に元の数値を合計したことになります。なんという無駄な計算!この方法では、平方根が計算できない負の数は扱えないので注意が必要ですね(笑)。
=SUMIF(A1:B3,"<>")
SUMIF関数で、条件に「”<>”(空白ではない)」を指定する方法。
範囲内に空白セルがなければ、結果的にすべての数値を合計することになり、実質SUM関数と同じ動きになります。
4. 複素数関数系 – 虚数の世界からの使者
考えかた
Excelには、虚数を含む「複素数」を扱うための専門関数があります。普段は全く使いませんが、合計のためだけに、彼らを呼び出してみましょう。
数式と解説
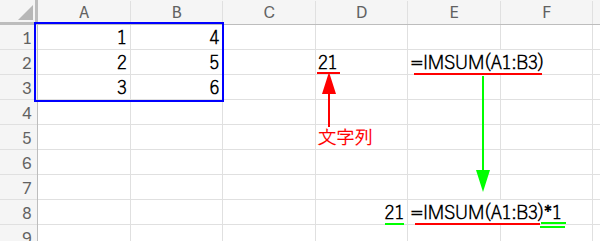
=IMSUM(A1:B3)*1
IMSUM関数は、複素数を合計する関数。普通の数値を渡すと、それを虚数部が0の複素数として扱い、合計してくれます。
結果は"21"のような文字列になるので、最後に「*1」をして数値に戻すのがポイントです。
=IMSUB(IMSUB(IMSUB(IMSUB(IMSUB(A1,-A2),-A3),-B1),-B2),-B3)*1
複素数には、引き算を行うIMSUB関数もあります。
これを利用し、「A1から-A2を引き、その結果から-A3を引き…」と、マイナスの数値を延々と引き続けることで、結果的に足し算を実現しています。非常に遠回りです!

5. 行列計算 – 数学の力、見せてやる!
考えかた
Excelは、行列の掛け算を行うMMULT関数も搭載しています。
これを使えば、行ごとの合計を出し、最後にそれらを合計する、という2段階の計算を一発で行えます。
数式と解説
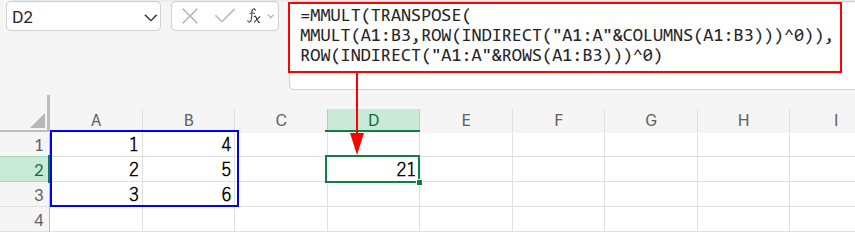
=MMULT(TRANSPOSE(MMULT(A1:B3,ROW(INDIRECT("A1:A"&COLUMNS(A1:B3)))^0)),ROW(INDIRECT("A1:A"&ROWS(A1:B3)))^0)
この数式は、2回のMMULTで値を畳み込んでいます。
1. MMULT(A1:B3, {1;1}): まず、3×2の行列に、2×1の「1だけの行列」を掛けて、行ごとの合計 {5;7;9} を計算します。

2. MMULT({5,7,9}, {1;1;1}): 次に、先ほどの結果をTRANSPOSEで行列を入れ替え、今度は3×1の「1だけの行列」を掛けて、すべての合計「21」を計算します。

ROW(...)^0は、「1だけの行列」を作り出すための、古典的なテクニックです。
6. 対数系 – 指数と対数の美しい関係
考えかた
数学の世界では、log(a*b) = log(a) + log(b) という法則があります。
これを逆手に取り、足し算を掛け算の世界で実現します。
数式と解説
=POWER(10,MAX(LOG10(A1:B3)))*SUMPRODUCT(POWER(10,LOG10(A1:B3)-MAX(LOG10(A1:B3))) )
この数式は、コンピュータが小数を扱う際の誤差(浮動小数点誤差)を避けるための、非常に高度なテクニックです。
各数値を最大値で割って正規化し、後で元に戻すことで、より正確な合計を求めています。
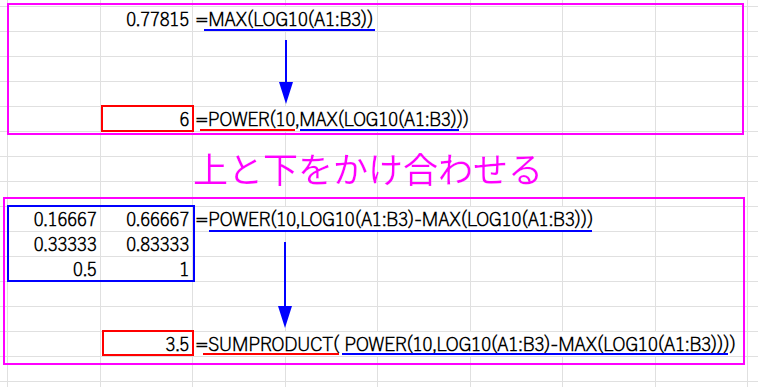
ただし、対数(LOG10)を使うため、この方法も正の数でしか使えません。
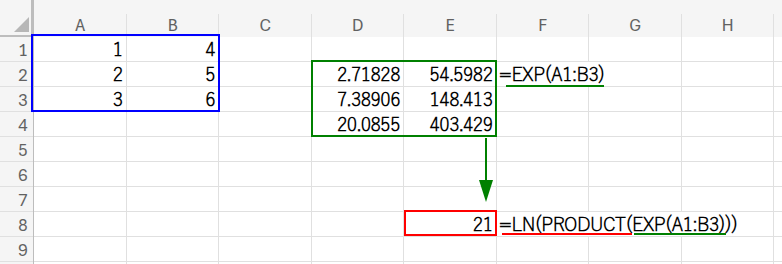
=LN(PRODUCT(EXP(A1:B3)))
この数式は、LN(e^1 * e^4 * e^2 * ...) という計算をしています。
指数の法則により、これは LN(e^(1+4+2+...)) となり、自然対数(LN)と指数関数(EXP)が互いを打ち消し合うことで、最終的に指数部分の合計 1+4+2+... だけが残るのです!
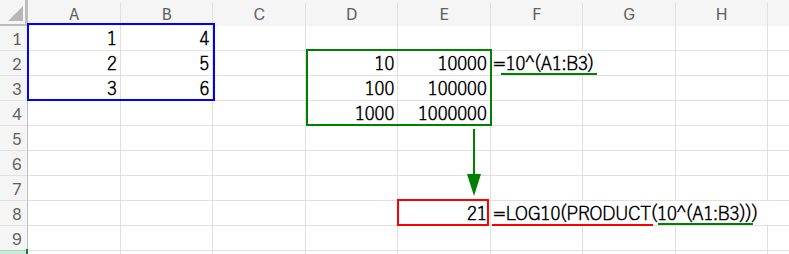
=LOG10(PRODUCT(10^(A1:B3)))
こちらは、常用対数(LOG10)と10のべき乗を使ったバージョン。
やっていることは上と全く同じですが、こちらの方がより直感的かもしれません。
筆者としては、この数式が数学的に最も美しいと感じます。
7. 財務関数系 – 異世界からの刺客
考えかた
投資の価値計算などに使われる「財務関数」。
全く畑違いに見えますが、彼らの計算式をハックすれば、合計ができてしまうのです!
数式と解説
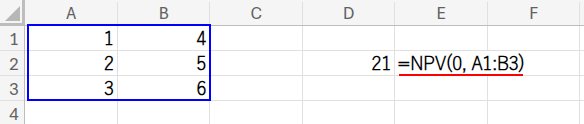
=NPV(0,A1:B3)
NPV(正味現在価値)関数は、NPV(利率, 値1, [値2], ...) のように使います。
将来の一連のキャッシュフローを、指定した「利率」で割り引いて、現在の価値の合計を計算します。

しかし、その「利率」を「0」にすると、割引が一切行われず、単純な数値の合計になる、という驚きの裏ワザです!
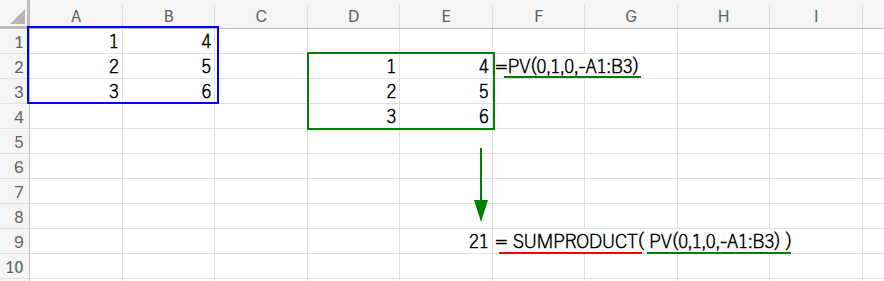
=SUMPRODUCT(PV(0,1,0,-A1:B3))
PV(現在価値)関数は、PV(利率, 期間, 定期支払額, [将来価値], [支払期日]) と、多くの引数を取ります。

ここでは、利率を「0」、期間を「1」、定期支払額を「0」に固定し、[将来価値]にマイナスを付けた範囲を入れることで、各セルの値をプラスに戻しています。それを最後に合計しています。
=PV(0,1,PMT(0,1,0,NPV(0,A1:B3)))
NPVで合計し、それをPMT(定額返済額)関数でマイナスの値に変え、最後にPVでプラスに戻すという、もはや何がしたいのか分からない、芸術的な無駄遣いです!
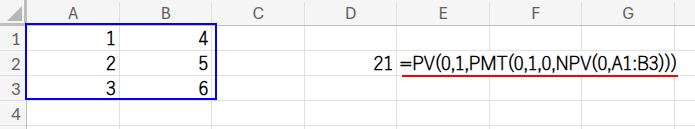
8. 比較的新しい関数 – 現代の解法
考えかた
最後に、Excel 2019以降やMicrosoft 365で使える、比較的新しい関数を使った方法も見てみましょう。
数式と解説
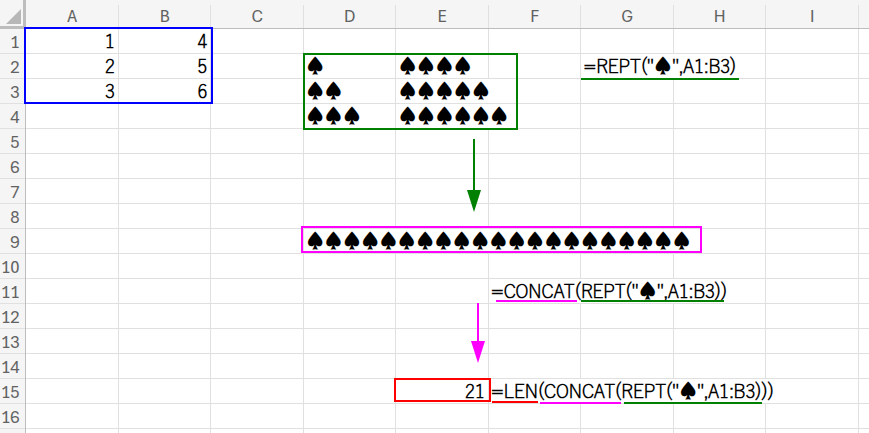
=LEN(CONCAT(REPT("♠",A1:B3)))
これは第1弾でも登場した、文字列操作の力技ですね。
REPT関数で各数値の数だけトランプのスペードを作り、CONCAT関数(Excel 2019以降)でそれらを全て連結し、最後にLEN関数で文字数を数えることで合計としています。
この方法も、負の数や小数が扱えませんね。
=REDUCE(0,A1:B3,LAMBDA(a,b, a+b))
Microsoft 365ユーザー限定ですが、これぞ現代の合計の形かもしれません。
REDUCE関数は、REDUCE(初期値, 配列, LAMBDA(累積値, 現在値, 計算式)) のように使います。
「初期値0」からスタートし、配列(A1:B3)の値を一つずつ取り出し(現在値 b)、前のステップまでの計算結果(累積値 a)に、足し込んでいく(a+b)という処理を、非常にスマートに記述しています。

まとめ:合計への道は、一つじゃない!
たった一つの「合計」というゴールに対して、これほどまでに多様で、奇妙で、そして美しいアプローチが存在することに、楽しんでいただけたのではないでしょうか。
実務でSERIESSUM関数を使う日は、おそらく永遠に来ないでしょう(笑)
しかし、今回挑戦した関数パズルたちは、決して無駄ではありません。
これらの難解な数式を理解しようとすることで、Excelの各関数の持つ本当の力や、その背景にある数学的な法則を、より深く知ることができます。
その知識は、いつかあなたがもっと複雑な問題に直面したとき、きっと新しい解決策への扉を開いてくれるはずですよ!