- はじめに:ただの「1」、されど「1」。その作り方、いくつ知っていますか?
- 準備:ゴールを確認する
- 10のアプローチで、「1の配列」を攻略せよ!
- アプローチ1:配列定数 – 最も原始的な方法
- アプローチ2:ROW + INDIRECT + べき乗 – 古典的テクニックの王道
- アプローチ3:OFFSET + ISERROR + ISLOGICAL – IFERRORなき時代の知恵
- アプローチ4:IFERROR – エラー処理の逆用
- アプローチ5:FACT + INDEX + MUNIT – 数学的トリック
- アプローチ6:SEQUENCE – 現代のスタンダード
- アプローチ7:RANDARRAY – ランダムの逆説
- アプローチ8:MAKEARRAY + LAMBDA – 無からの創造
- アプローチ9:VSTACK – シンプルすぎる合体
- アプローチ10:TEXTSPLIT + REPT – 文字列からの錬金術
- まとめ:回り道こそ、最大の近道だ!
はじめに:ただの「1」、されど「1」。その作り方、いくつ知っていますか?
Excelで数式を組んでいると、時々、こんな配列が欲しくなる瞬間、ありませんか?
={1;1;1;1;1}
そう、ただひたすらに「1」が縦に並んだ配列です。

例えば、行列計算を行うMMULT関数などで、特定の行や列だけを合計したい時に、この「1だけの配列」が、まるで魔法の杖のように活躍することがあります。
「え、そんなの {1;1;1;1;1} って直接書けばいいじゃない?」
そう思ったあなた、大正解!
多くの場合、それが最も手っ取り早い方法です。
でも、ちょっと待ってください!
もし、もっとたくさんの「1」が必要になったら?もし、この配列を「数式」だけで、スマートに生成できたとしたら?
Excel 97よりも前の、遥か昔から使える超古典的なテクニックから、最新のLAMBDA関数を使った方法まで。
Excelの進化の歴史を辿りながら、それぞれの関数の個性的な挙動を探求していきますよ!
目的は、
配列を生成するための多様なアプローチを知り、関数の本質的な理解を深めること!
なぜ、便利な新関数があるのに、わざわざ古い関数で苦労するのか?
それは、基本的な関数の組み合わせの中にこそ、ロジックの本質が隠されているからです。
新関数は便利ですが、その内部処理はブラックボックスになりがち。根源を知ることで、応用力は格段にアップします!
この関数パズルを通して、あなたの「関数の引き出し」が、さらに豊かになるかもしれません!
本記事では、無料のWeb版Excelを使用して検証および画像の作成を行っています。Windowsはもちろん、MacやLinuxの方もブラウザさえあれば挑戦できます!
準備:ゴールを確認する
何事も、まずは準備から。まっさらなシートを用意してください。
私たちのゴールは、例えばA1セルに数式を一つ入力するだけで、A1からA5セルにかけて、以下のように「1」が表示されることです。
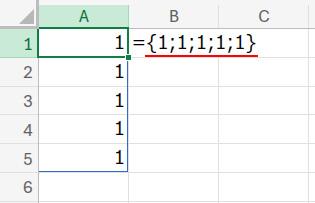
さあ、このシンプルなゴールに向かって、10の異なる道を冒険しましょう!
10のアプローチで、「1の配列」を攻略せよ!
関数の詳細な仕様については、Microsoft公式のヘルプも参考にしてください。
今回は、Excelの古いバージョンでも動作する可能性が高い順に、数式を紹介していきます。
アプローチ1:配列定数 – 最も原始的な方法
【動作確認バージョン:Excel 97 以前】
考えかた
関数すら使わない、最も直接的な方法です。配列そのものを、波括弧{}を使って直接書き込んでしまいます。
数式と解説
={1;1;1;1;1}
・{...}: これは「配列定数」と呼ばれるもので、配列を直接数式内に記述する方法です。
・; (セミコロン): 配列定数の中で、セミコロンは「次の行へ」を意味します。これにより、縦一列の配列が生成されます。(ちなみにカンマ,は「次の列へ」を意味します)
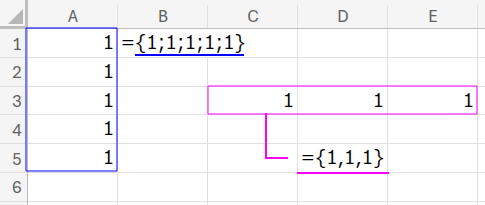
シンプルですが、100個の「1」が必要になったら、書くのが大変そうですね(笑)。
アプローチ2:ROW + INDIRECT + べき乗 – 古典的テクニックの王道
【動作確認バージョン:Excel 97 以前】
考えかた
Excelの古き良き時代から伝わる、連番生成の定番テクニックを応用します。
まず連番を作り、それを「0乗」することで、すべて「1」に変えてしまいます。
数式と解説
=ROW(INDIRECT("A1:A"&ROWS(A1:A5)))^0
1. ROWS(A1:A5): まず、ROWS関数で、対象範囲(今回はA1:A5)の行数「5」を計算します。
これにより、配列のサイズが変わっても数式が対応できるようになります。
2. "A1:A" & ...: 計算した行数「5」と文字列を連結し、"A1:A5" という文字列を作ります。
3. INDIRECT(...): 次に、INDIRECT関数が、この文字列 “A1:A5” を本物のセル参照 A1:A5 に変換します。
4. ROW(...): そして、ROW関数が、その参照範囲 A1:A5 の各行の行番号を取得し、{1;2;3;4;5} という連番配列を生成します。
5. ... ^ 0: 最後に、この連番配列の各要素を「0乗」します。
数学のルールで、「0以外のどんな数も0乗すれば1になる」ので、結果として {1;1;1;1;1} という配列が生まれるのです!2025年の現代だからこそ、覚えておきたい美しい技ですね。

アプローチ3:OFFSET + ISERROR + ISLOGICAL – IFERRORなき時代の知恵
【動作確認バージョン:Excel 97 以前】
考えかた
まだIFERROR関数が存在しなかったExcel 97以前の時代。
当時の情報系関数(IS系)と、古くから存在するOFFSET関数を組み合わせて、「1」の配列を作り出す猛者がいました。(多分いません。私だけです…)
数式と解説
=ISLOGICAL(ISERROR(OFFSET(A1,0,0,5)))*1
1. OFFSET(A1,0,0,5): まず、OFFSET関数で、A1セルを起点に、高さ5、幅1のセル範囲への参照(メモリ上の仮想的な参照)を作ります。
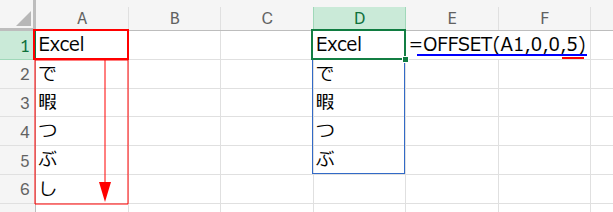
2. ISERROR(...): 次に、ISERROR関数で、この参照範囲がエラーかどうかを判定します。有効な参照なので、結果は {FALSE;FALSE;FALSE;FALSE;FALSE} という配列になります。
仮にエラーがあってもTRUEを返します。
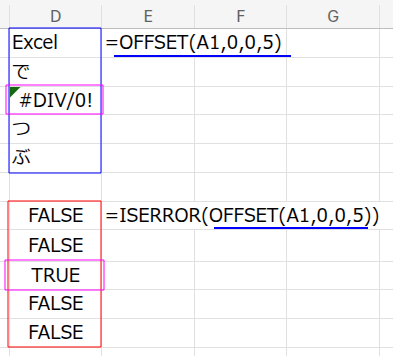
3. ISLOGICAL(...): さらに、ISLOGICAL関数で、この結果が論理値(TRUE/FALSE)かどうかを判定します。すべて論理値なので、{TRUE;TRUE;TRUE;TRUE;TRUE} という配列に変わります。

4. ... * 1: 最後に、このTRUE/FALSE配列に1を掛けることで、TRUEが「1」に変換され、目的の配列が完成します。

アプローチ4:IFERROR – エラー処理の逆用
【動作確認バージョン:Excel 2007 以降】
考えかた
Excel 2007で登場したIFERROR関数。本来はエラーを別の値に置き換えるための関数ですが、これを逆用して「1」の配列を作ります。
数式と解説
=IFERROR(A1:A5=A1:A5,1)*1
1. A1:A5=A1:A5: まず、A1:A5の範囲(中身は空でもOK)と自分自身を比較します。
結果は {TRUE;TRUE;TRUE;TRUE;TRUE} という配列になります。
ただし、A1:A5の範囲にエラーがあった場合、エラー値が返ります。
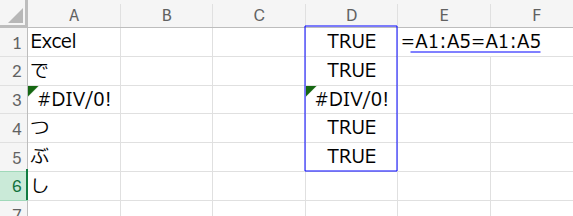
2. IFERROR(..., 1): IFERROR関数は、第1引数がエラーでなければその値を、エラーであれば第2引数の値を返します。
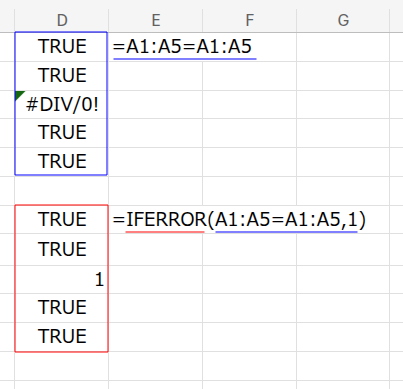
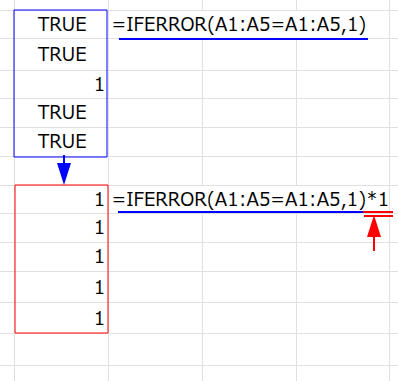
3. ... * 1: 最後に1を掛けて、TRUEを「1」に変換します。
アプローチ5:FACT + INDEX + MUNIT – 数学的トリック
【動作確認バージョン:Excel 2013 以降】
考えかた
Excel 2013で導入された行列関数MUNITと、階乗を計算するFACT関数を組み合わせた、非常に数学的で面白いアプローチです。
数式と解説
=FACT(INDEX(MUNIT(5),,1))
1. MUNIT(5): まず、MUNIT関数で、5×5の「単位行列」(対角線上が1で、他は0の行列)を生成します。
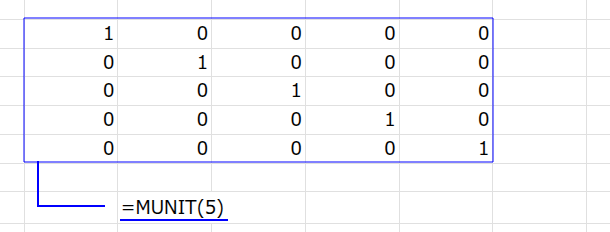
2. INDEX(..., ,1): 次に、INDEX関数で、この単位行列の「1列目」だけを抜き出します。結果は {1;0;0;0;0} という配列になります。
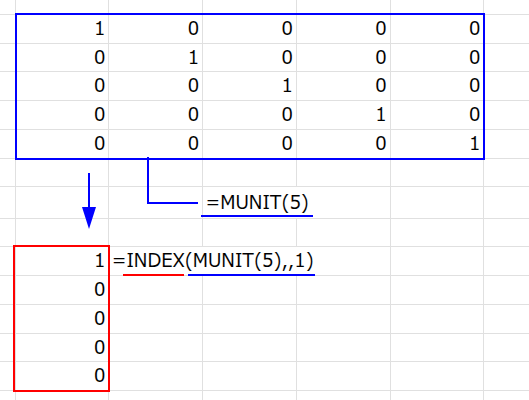
3. FACT(...): 最後に、この配列の各要素の階乗をFACT関数で計算します。

数学のルールで、「1の階乗(1!)は1」、「0の階乗(0!)も1」なので、結果として {1;1;1;1;1} という配列が生まれるのです!面白いですよね!
アプローチ6:SEQUENCE – 現代のスタンダード
【動作確認バージョン:Excel 2021 以降】
考えかた
Excel 2021以降(Microsoft 365含む)で導入されたSEQUENCE関数。
連番生成の決定版ですが、引数を工夫すれば「1だけの配列」も簡単に作れます。
数式と解説
=SEQUENCE(5,,,0)
SEQUENCE関数は SEQUENCE(行数, [列数], [開始], [ステップ]) のように使います。
・SEQUENCE(5, ...): まず、5行の配列を作ると指定します。
・..., , ,0): 第4引数「ステップ」に「0」を指定するのがポイントです。
これにより、第3引数「開始」(省略時は1)の値が、ステップ0で、つまり全く変化せずに5回繰り返されるため、{1;1;1;1;1} が生成されるのです。

SEQUENCE関数が使用できないExcel 2019以前を使用している場合、以下の記事で代替数式を紹介しています!
アプローチ7:RANDARRAY – ランダムの逆説
【動作確認バージョン:Excel 2021 以降】
考えかた
同じくExcel 2021以降で導入されたRANDARRAY関数。ランダムな数を生成する関数ですが、「1以上1以下のランダムな整数」を指定すれば…?
数式と解説
=RANDARRAY(5,,1,1)
RANDARRAY関数は RANDARRAY([行数], [列数], [最小値], [最大値], [整数]) のように使います。

第5引数を省略すると小数を返します。
・RANDARRAY(5, , 1, 1): 5行1列で、最小値「1」、最大値「1」の「小数」の乱数を生成しなさい、という命令です。
1以上1以下の数はそもそも「1」しか存在しないため、結果として {1;1;1;1;1} が返ってくる、という逆説的なアプローチです。

アプローチ8:MAKEARRAY + LAMBDA – 無からの創造
【動作確認バージョン:Microsoft 365】
考えかた
Microsoft 365で使えるようになったLAMBDA関数ファミリー。
その一員であるMAKEARRAY関数を使えば、「指定したサイズの配列の、すべての要素に『1』を入れる」という処理を、非常に直感的に記述できます。
数式と解説
=MAKEARRAY(5,,LAMBDA(r,c,1))
・MAKEARRAY(5, , ...): MAKEARRAY関数は MAKEARRAY(行数, 列数, LAMBDA(...)) のように使います。まず、5行1列の配列を作ると宣言します。
・LAMBDA(r,c,1): 次に、その配列の各要素の値を決めるルールをLAMBDA関数で定義します。
「r」(行番号)と「c」(列番号)を引数として受け取りますが、今回はそれらを使わずに、単純に「1」という値を返す、と指定しています。
これにより、すべての要素が1の配列が生成されるのです。

アプローチ9:VSTACK – シンプルすぎる合体
【動作確認バージョン:Microsoft 365】
考えかた
Microsoft 365のVSTACK関数。本来は複数の配列を縦に連結するための関数ですが、引数に配列ではなく、単一の「1」を5回指定したら…?
数式と解説
=VSTACK(1,1,1,1,1)
VSTACK関数は、引数を順番に縦に積み重ねてくれます。
まさに、「小包1つを大型トラックで運ぶ」ような、関数の役不足感が否めませんが、これも立派な一つの方法ですね(笑)。

アプローチ10:TEXTSPLIT + REPT – 文字列からの錬金術
【動作確認バージョン:Microsoft 365】
考えかた
Microsoft 365の文字列操作関数TEXTSPLITを使った方法です。「1」と区切り文字を繰り返した文字列を作り、それを区切り文字で分割することで、「1」だけの配列を生成します。
数式と解説
=TEXTSPLIT(REPT("1-",4)&1,,"-")*1
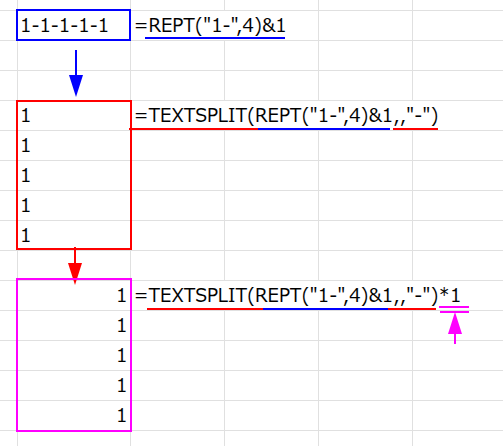
1. REPT("1-",4)&1: まず、REPT関数で “1-” を4回繰り返し、最後に “1” を連結して、"1-1-1-1-1" という文字列を作ります。

2. TEXTSPLIT(..., ,"-"): 次に、TEXTSPLIT関数の第3引数「列区切り文字」を省略し、第4引数「行区切り文字」に「–」を指定します。
これにより、文字列が「-」で分割され、{"1";"1";"1";"1";"1"} という縦一列の「文字列」の配列が生成されます。
3. ... * 1: 最後に、1を掛けて、文字列の配列を数値の配列に変換します。
まとめ:回り道こそ、最大の近道だ!
たった一つのシンプルなゴールに対して、これほどまでに多様なアプローチが存在することに、驚かれたのではないでしょうか。
Excel 97以前の知恵から、最新のLAMBDA関数まで。それぞれの数式に、それぞれの時代の工夫と美学が詰まっています。
もちろん、FILTERXML関数(Windows版Excel 2013以降)のような、さらにマニアックな方法も存在しますし、新関数を使えばこれ以外にもまだまだ作れるはずです!
興味のある方は、ぜひあなただけの「1の配列生成式」を探求してみてください!
一見、無駄に見える「回り道」こそが、実は関数の本質的な理解へとつながる、最大の近道なのかもしれません。
今回の関数パズルが、皆さんのExcelへの知的好奇心をさらに深めるきっかけになれば、これほど嬉しいことはありません。