- 大文字「A」、小文字「a」、見落としていませんか?
- 準備:挑戦者となるリスト
- 7つのアプローチで、「A or a」を攻略せよ!
- まとめ:文字列操作は、ロジックの宝庫だ!
大文字「A」、小文字「a」、見落としていませんか?
Excelでデータリストを管理しているとき、こんな場面はありませんか?
「この商品リストの中で、『A』か『a』が名前に含まれる商品は、全部で何個あるんだろう?」
大文字と小文字が混在しているデータを正しく集計する…。
これは、実務でも非常によく出くわす、重要で厄介な問題です。
「COUNTIFのワイルドカードでできる…?あれ、でも大文字と小文字は…?」
そんな、あなたの「?」にお答えするのが、今回の冒険です!
今回は、「“A”または”a” が含まれているセルはいくつありますか?」というテーマで、実に7種類もの異なるアプローチでこの問題に挑みます。
【最重要ポイント!】
今回のミッションは、「a」や「A」という文字が全部で何個あるか(延べ出現回数)を数えることではありません。
例えば「Pineapple」には「a」が1つ、「Banana」には「a」が3つありますが、どちらも「1セル」としてカウントします。あくまでも、「その文字が含まれているセルの数」を数えるのがゴールです!
文字列操作の基本から、配列計算の応用まで。この冒険が終わる頃には、あなたのExcelスキルが、また一つ上のステージへと進化しているかもしれませんよ!
本記事では、無料のWeb版Excelを使用して検証および画像の作成を行っています。Windowsはもちろん、MacやLinuxの方もブラウザさえあれば挑戦できます!
準備:挑戦者となるリスト
何事も、まずは準備から。まっさらなシートのA1セルを起点に、以下の7行1列のリストを作成してください。
以下の数式をA1セルに貼り付けます。
={"商品";"Peach ";"Apricot";"Melon";"Pineapple";"Blueberry ";"Banana"}
ゴールは、A2:A7の範囲の中から、「A」または「a」が含まれるセル、すなわち「Peach 」「Apricot」「Pineapple」「Banana」の合計「4」セルを、数式で導き出すことです。
7つのアプローチで、「A or a」を攻略せよ!
関数の詳細な仕様については、Microsoft公式のヘルプも参考にしてください。
アプローチ1:COUNTIF + ワイルドカード(王道)
考えかた
まずは、文字列検索の王道、COUNTIF関数から参りましょう。
COUNTIF関数は、特定の文字を含むセルを数えるために、「ワイルドカード」という便利な記号を使うことができます。
【ワイルドカードとは?】
・* (アスタリスク): 0文字以上の、任意の文字列を表します。(例: "*a*" → “a”だけでも “Banana” でも “Apricot” でもOK)
・? (クエスチョンマーク): 任意の1文字を表します。(例: "a?e" → “are” には一致するが、 “apple” には一致しない)
数式と解説
=COUNTIF(A2:A7,"*a*")
・A2:A7: 検索する範囲を指定します。
・"*a*": これが検索条件です。「0文字以上の何かが来て、そのあとに『a』が来て、そのあとに0文字以上の何かが来る」という意味になります。
つまり、「どこでもいいから “a” が含まれている」という条件になります。
ここで素晴らしいのは、COUNTIF関数のワイルドカード検索は、大文字と小文字を区別しないことです。
そのため、"*a*"と指定するだけで、「a」も「A」も両方見つけ出し、正しく「4」という答えを返してくれます。
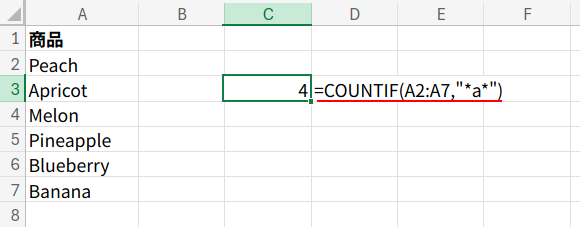
Excel初心者を脱却する上で、まず最初に覚えたい必須テクニックですね!
Windowsのファイル検索などもそうですが、コンピュータの世界では『大文字と小文字を区別しない』のがデフォルトの優しさなんです。でも、Excelで厳密にやりたい時はそれが仇になります(笑)
アプローチ2:COUNT + SEARCH(大文字小文字を区別しない検索)
考えかた
COUNTIFを使わない方法です。Excelには、文字列を探すための専門家が2人います。
そのうちの一人、SEARCH関数の出番です。
数式と解説
=COUNT(SEARCH("a",A2:A7))
この数式、内側から見ていきましょう。
1. SEARCH("a",A2:A7): SEARCH関数は、SEARCH(検索文字列, 対象) のように使います。
この関数の最大の特徴は、「大文字と小文字を区別しない」ことです。
A2:A7の範囲に対して「a」を探しに行くと、見つかったセルにはその位置(数値)を、見つからなかったセルには #VALUE! エラーを返します。
結果は {3;1;#VALUE!;5;#VALUE!;2} という、数値とエラーが混在した配列になります。
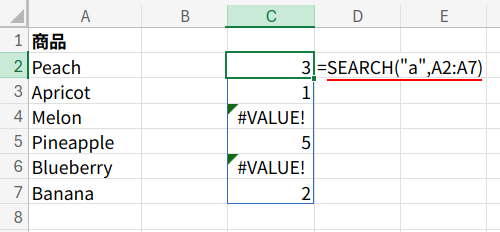
2. COUNT(...): 最後に、COUNT関数がこの配列を数えます。
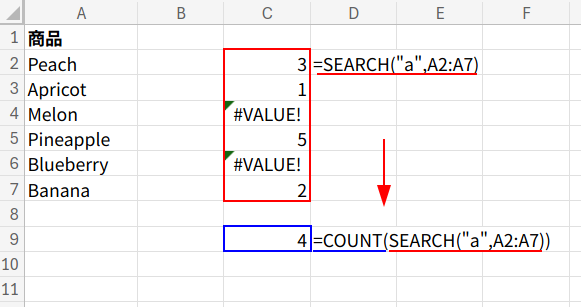
COUNT関数は、数値だけをカウントし、エラー値や文字列は無視するという性質を持っています。
そのため、エラーにならなかった(=「a」か「A」が見つかった)セルの個数、すなわち「4」を正確に返してくれるのです!
アプローチ3:COUNT + FIND + LOWER(大文字小文字を区別する検索)
考えかた
文字列を探す専門家、もう一人はFIND関数です。
SEARCH関数との決定的な違いは、「大文字と小文字を厳密に区別する」ことです。
この性質を理解した上で、あえてFIND関数を使ってみましょう。
数式と解説
=COUNT(FIND("a",LOWER(A2:A7)))
1. LOWER(A2:A7): そのままFIND("a", ...)とすると、「Apricot」の「A」が見つからず、正しい答えになりません。
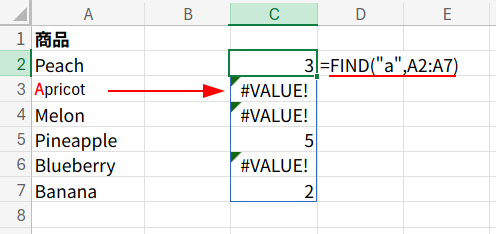
そこで、LOWER関数の出番です。LOWER関数は、すべてのアルファベットを強制的に「小文字」に変換します。{"peach ";"apricot";...} という、すべてが小文字の仮想的な配列を作り出します。
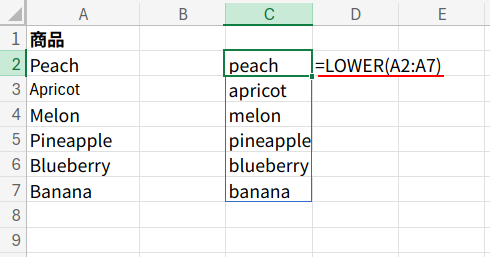
2. FIND("a", ...): これで安心!すべて小文字になった配列に対して、FIND関数で「a」を探しに行きます。
SEARCH関数と同様に、見つかれば位置(数値)、見つからなければ #VALUE! エラーを返します。結果は {3;1;#VALUE!;5;#VALUE!;2} となります。
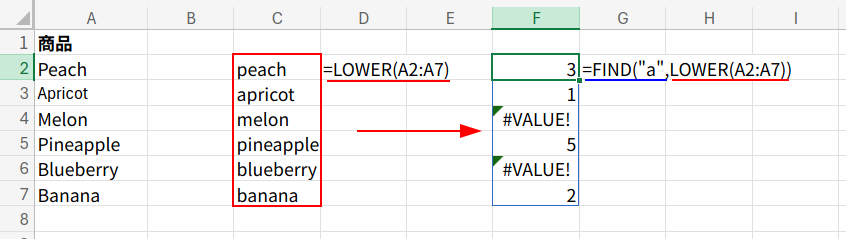
3. COUNT(...): 最後に、COUNT関数が数値の個数だけを数え、「4」を返します。SEARCHとFINDの違い、よく分かりましたね!

アプローチ4:SUM + ISNUMBER + FIND + 配列定数 (条件あり)
考えかた
もし、「a」と「A」だけでなく、「e」や「E」も同時に探したい…となったらどうでしょう?
そんな時に応用できるのが、配列定数 {"a","A"} を使うテクニックです。
【注意点】
この数式は、「a」と「A」の両方を含むセル(例: “Alphabet”)があると、「2」とカウントしてしまいます。これは「セルの数」ではなく「ヒットした回数」を数えているためです。
もし、両方含まれていても「1」とカウントしたい場合は、アプローチ7で紹介するMMULT関数を使った方法が、より完璧なロジックになります。
数式と解説
=SUM(ISNUMBER(FIND({"a","A"},A2:A7))*1)
1. FIND({"a","A"},A2:A7): ここが超重要!FIND関数(大文字小文字を区別)に、検索文字列として {"a","A"} という配列を渡します。
すると、ExcelはA2:A7の各セルに対して、「a」を探した場合の結果と、「A」を探した場合の結果を、両方計算します。結果として、6行2列の、数値とエラーが混在した配列が生まれます。
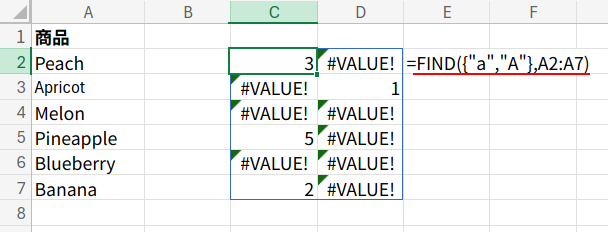
2. ISNUMBER(...): ISNUMBER関数が、この6×2の配列をチェックし、数値(見つかった場所)をTRUE、エラー(見つからなかった場所)をFALSEに変換します。
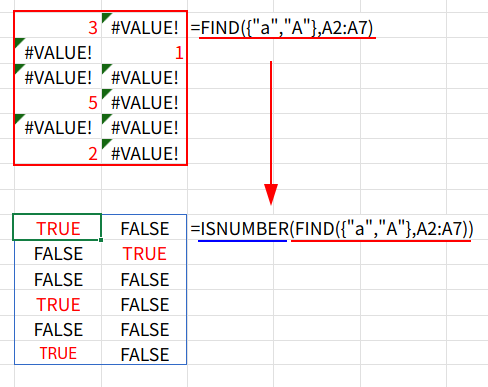
3. ... * 1: TRUE/FALSEを 1/0 の数値に変換します。

4. SUM(...): 最後に、SUM関数が、この6×2の配列に含まれる「1」をすべて合計します。
今回のデータでは、「a」または「A」のどちらか一方しか含まれていないため、1+1+1+1 = 4 と正しく計算されます。

アプローチ5:SUBSTITUTE + UPPER(置換して比較)
考えかた
これは、非常に賢いロジックです。
「もし文字列に『A』が含まれているなら、『A』を全部消した文字列は、元の文字列と長さが変わるはずだ!」という考え方です。
文字列そのものを比較するより、文字数という数値を比較したほうが視覚的にわかりやすいですよね。
数式と解説
=SUM((LEN(UPPER(A2:A7))<>LEN(SUBSTITUTE(UPPER(A2:A7),"A","")))*1)
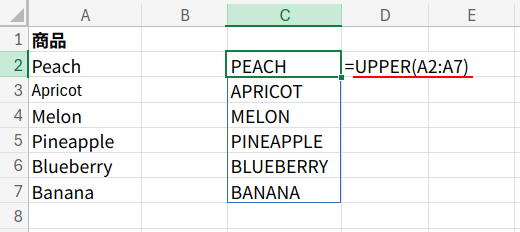
1. UPPER(A2:A7): まず、UPPER関数ですべてを大文字に統一します({"PEACH ";"APRICOT";...})。
SUBSTITUTE関数はFIND関数と同様に大文字と小文字を区別するため、この下準備が必須です。
2. SUBSTITUTE(...,"A",""): SUBSTITUTE関数(SUBSTITUTE(文字列, 検索文字列, 置換文字列))を使って、大文字化された配列から「A」をすべて「””」(空白)に置換(削除)します。(例: “PINEAPPLE” → “PINEPPLE”)
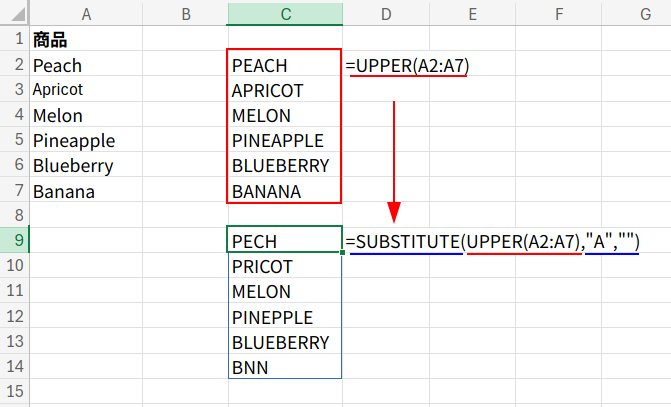
3. LEN(UPPER(...)) <> LEN(SUBSTITUTE(...)): 「元の文字列の長さ」と、「Aを削除した後の文字列の長さ」が、<>(等しくない)かどうかを比較します。

「A」が含まれていれば長さが変わりTRUE、含まれていなければ長さが変わらずFALSEになります。
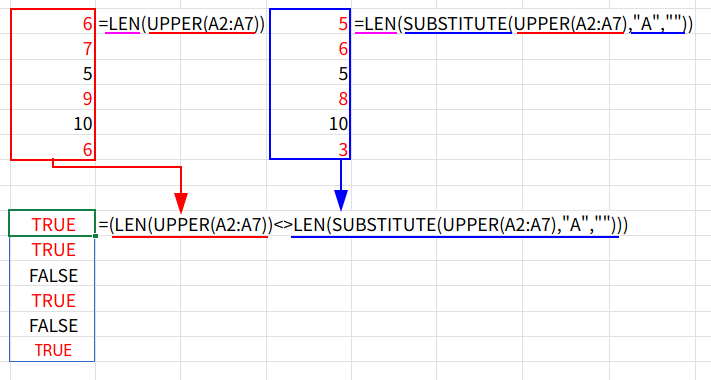
4. SUM(...*1): 最後に、TRUE(1)になったセルの数を合計します。

アプローチ6:SUBSTITUTE vs SUBSTITUTE(超巧妙なパズル)
考えかた
これは、アプローチ5のUPPER/LOWER関数さえも使わずに、SUBSTITUTE関数の「大文字と小文字を区別する」性質を最大限に利用した、超巧妙なロジックパズルです。
数式と解説
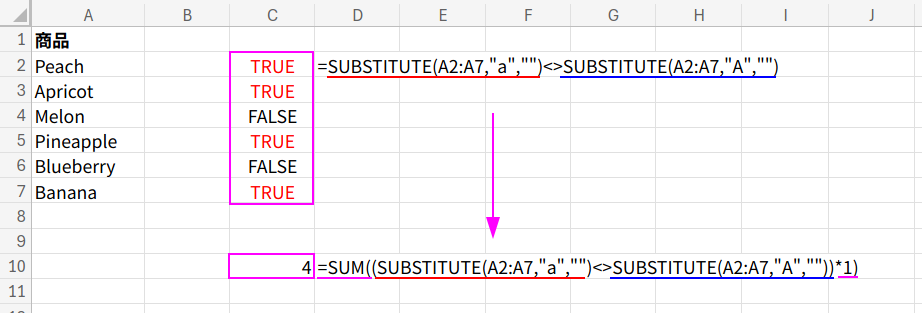
=SUM((SUBSTITUTE(A2:A7,"a","")<>SUBSTITUTE(A2:A7,"A",""))*1)
この数式がなぜ動くのか、3つのパターンで考えてみましょう。
・“Melon” (どちらも含まない):SUBSTITUTE("Melon","a","") → “Melon”SUBSTITUTE("Melon","A","") → “Melon”"Melon" <> "Melon" は FALSE です。
・“Peach ” (“a”のみ含む):SUBSTITUTE("Peach ","a","") → “Pech “SUBSTITUTE("Peach ","A","") → “Peach “"Pech " <> "Peach " は TRUE です。
・“Apricot” (“A”のみ含む):SUBSTITUTE("Apricot","a","") → “Apricot“SUBSTITUTE("Apricot","A","") → “pricot”"Apricot" <> "pricot" は TRUE です。
・(もし “Alphabet” があったら):SUBSTITUTE("Alphabet","a","") → “Alphbet“SUBSTITUTE("Alphabet","A","") → “lphabet“"Alphbet" <> "lphabet" は TRUE です。

つまり、”a”か”A”のどちらか(または両方)が含まれていれば、2つの置換結果は必ず異なる文字列になるため、TRUE(1)としてカウントできるのです!素晴らしいロジックですね。
アプローチ7:MID + SEQUENCE + MMULT(究極のセルカウント)
考えかた
最後は、実用性は皆無ですが、配列計算のロジックの極みとも言える方法です。
この方法は、アプローチ4で懸念された「もし”a”と”A”が同じセルに存在した場合(例: “Alphabet“)」でも、重複してカウントせず、「1セル」として正しく数えることができる、完璧な「セルカウント」数式です。
各セルを1文字ずつに分解し、その文字が “a”(または “A”)かを判定。
各セル(行)ごとに出現回数を合計した後、その合計が「0より大きい」かどうかを判定し、最後にセルの数を数えます。
数式と解説
=SUM((MMULT((MID(A2:A7,SEQUENCE(,MAX(LEN(A2:A7))),1)="a")*1,SEQUENCE(MAX(LEN(A2:A7)))^0)>0)*1)
この数式、内側から順に解き明かしていきましょう。
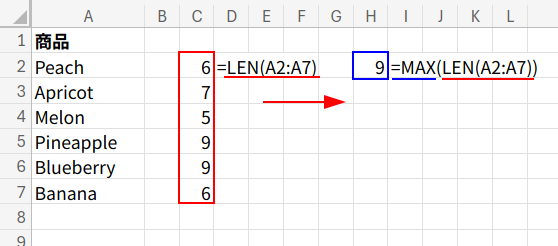
1. MAX(LEN(A2:A7)): まず、リスト内の最も長い文字列の文字数(今回は9文字)を取得します。
2. SEQUENCE(,9): {1,2,3,4,5,6,7,8,9} という横方向の連番配列を生成します。
3. MID(A2:A7, ..., 1): MID関数を使い、A2:A7の各セルを、1文字目から9文字目まで1文字ずつに分解します。
結果として、6行9列の巨大な文字の配列(2次元配列)がメモリ上に生成されます。
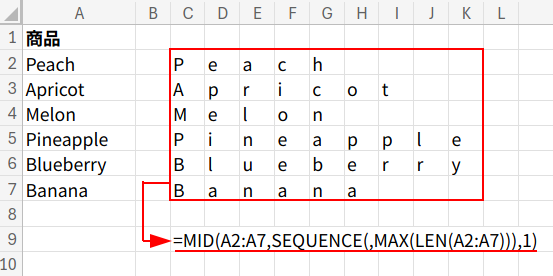
4. ... = "a": ここがポイント!3で作った文字の配列と、文字列 “a” を比較します。
Excelの比較演算子 = (イコール)は、大文字と小文字を区別しないため、”a” も “A” も両方とも TRUE と判定されます。
結果は、TRUE/FALSEの6行9列の配列になります。
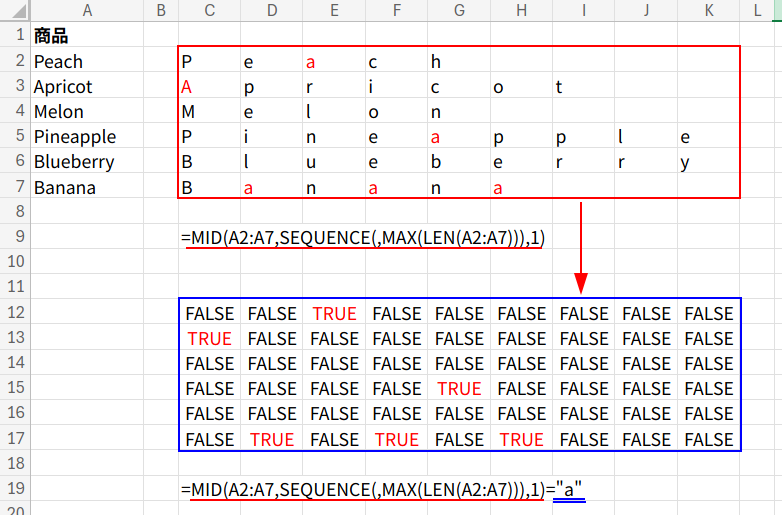
5. ... * 1: このTRUE/FALSEの配列に1を掛け、1(該当)と0(非該当)の数値配列に変換します。
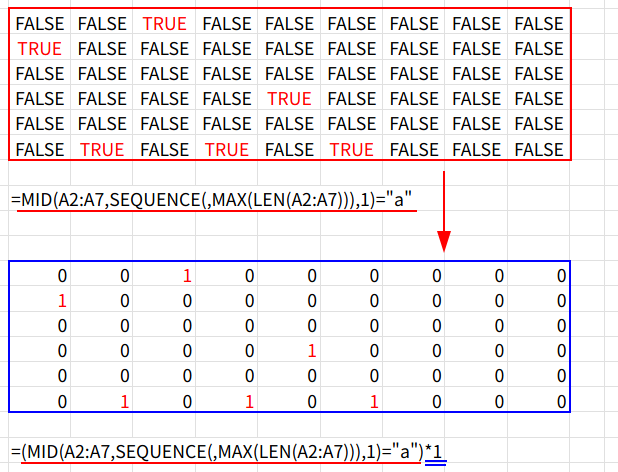
6. SEQUENCE(MAX(LEN(A2:A7)))^0: SEQUENCE(9)^0 という計算で、{1;1;1;1;1;1;1;1;1} という、列数(9)ぶんの「1」が縦に並んだ配列(乗数)を作ります。
7. MMULT( (1/0の配列) , (1の配列) ): MMULT(行列積)関数を使って、6行9列の「1/0の配列」と、9行1列の「1だけの配列」を掛け合わせます。
これにより、各行(元の各セル)の「1」が合計され、各セルに「a」か「A」が何個含まれているかの集計(例: “Banana”なら3)が{1;1;0;1;0;3}のように縦一列の配列として得られます。
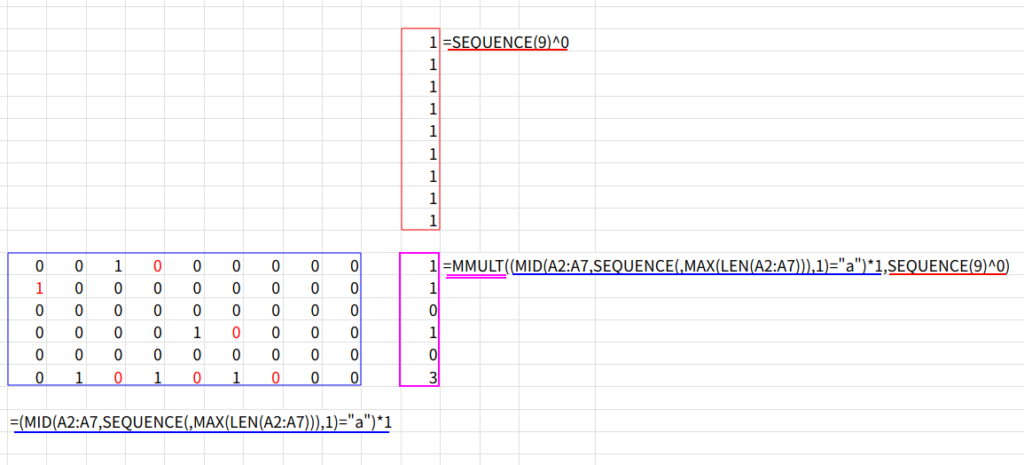
8. ... > 0: この集計結果が「0より大きい」かどうかを判定します。{1;1;0;1;0;3}は{TRUE;TRUE;FALSE;TRUE;FALSE;TRUE}に変わります。
この瞬間に、「出現回数」が「セルの有無」に変換されました!

9. SUM(...*1): 最後に、TRUE(1)の個数を合計し、完璧な答え「4」を導き出します。

まとめ:文字列操作は、ロジックの宝庫だ!
たった一つのシンプルなゴールに対して、これほどまでに多様なアプローチが存在することに、驚かれたのではないでしょうか。
実務で使うなら、大文字小文字を区別しない場合はアプローチ1のCOUNTIF、区別する場合はアプローチ2のCOUNT(SEARCH(…))が、最もシンプルで強力です。
しかし、他の関数パズルたちも、決して無駄ではありません。
FINDとSEARCHの違い、SUBSTITUTEの「大文字小文字を区別する」性質、そしてMMULTを使った配列の集計テクニック…。
これらの知識は、あなたの「Excel問題解決能力」を確実に引き上げてくれます。
今回の関数パズルが、皆さんのExcelへの知的好奇心をさらに深めるきっかけになれば、これほど嬉しいことはありません。
大文字小文字に関する記事は以下も参照ください。
Excel 大文字と小文字を区別して「比較」する7つの方法
Excel 大文字と小文字を区別して「検索」する7つの方法



