はじめに：その文字列、合計できますか？
Excelでデータを扱っていると、こんなリストに出会うこと、ありませんか？
「A3B2」
「C1D4」
「E5F6」
アルファベットと数値が入り混じった、謎のコード…。
「この文字列の中から、数値（3, 2, 1, 4…）だけを全部抜き出して、合計したい！どうすれば…？」
そんな、知的好奇心をくすぐるお悩みを、今回は「Excelで暇つぶし」流に、様々な角度から解決していきます！
今回のテーマは、「文字列から数値だけ抜き出して合計！」。
一見すると地味ですが、実はExcelの文字列操作と配列計算の奥深さがギュッと詰まった、非常に面白いパズルなのです。
この冒険を通して、あなたの「関数の引き出し」をさらに増やし、Excelの持つ無限の可能性を一緒に楽しんでいきましょう！なんだかワクワクしませんか？
本記事では、無料のWeb版Excelを使用して検証および画像の作成を行っています。Windowsはもちろん、MacやLinuxの方もブラウザさえあれば挑戦できます！
準備：挑戦者とルールを決める
何事も、まずは準備から。まっさらなシートのA1セルを起点に、以下の6行1列のリストを作成してください。
以下の数式をA1セルに貼り付けます。
={"コード";"A3B2";"C1D4";"E5F6";"G7H8";"I9J0"}
ゴールは、A2:A6の範囲の文字列に含まれるすべての数値を合計した「45」（=3+2+1+4+5+6+7+8+9+0）を、一つの数式で導き出すことです。
【今回の特別ルール】
今回の冒険では、ロジックの理解を最優先します！そのため、いくつかの前提条件を設けています。
1. 文字列は大文字のアルファベットと数値だけで構成されている。
2. 各セルの文字列は、すべて4文字である。（これにより、数式内でMAX(LEN(A2:A6))のような複雑なことをせず、「4」と直接書き込むことができます！）
6つのアプローチで、「数値合計」を攻略せよ！
さあ、6つの異なるロジックで、この難題に挑みましょう！
アプローチ1：MID + SEQUENCE + IFERROR（王道の分解）
考えかた
最も直感的な方法です。まず、すべての文字列を1文字ずつバラバラに分解します。
次に、それらを数値に変換しようと試み、文字（アルファベット）はエラーになるので、そのエラーを「0」に置き換えて、最後に全部合計します。
数式と解説
=SUM(IFERROR(MID(A2:A6,SEQUENCE(,4),1)*1,0))
1. SEQUENCE(,4): まず、{1,2,3,4}という横方向の配列（列番号）を作ります。これが「何文字目を抜き出すか」の指示書になります。
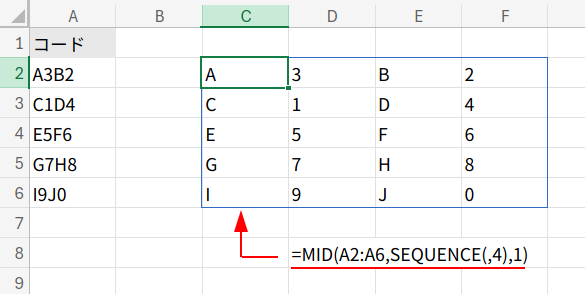
2. MID(A2:A6, ..., 1): MID関数を使い、A2:A6の各セル（5行）に対して、1文字目、2文字目、3文字目、4文字目をそれぞれ抜き出します。
Excelのスピル機能により、結果は 5行4列の文字の配列（2次元配列）になります。{"A","3","B","2"; "C","1","D","4"; ...}
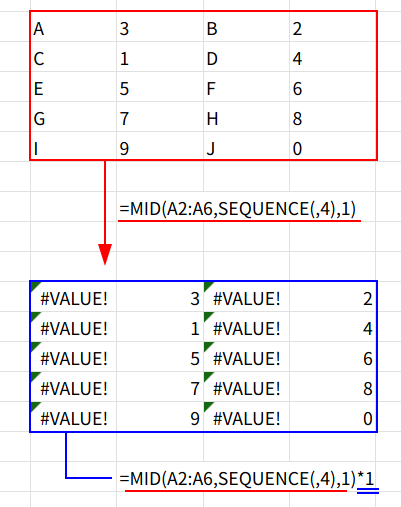
3. ... * 1: この文字の配列全体に「1」を掛け算します。Excelは、数値に変換できる文字（”3″など）は数値（3）に変換し、変換できない文字（”A”など）は #VALUE! エラーを返します。{#VALUE!, 3, #VALUE!, 2; #VALUE!, 1, #VALUE!, 4; ...}
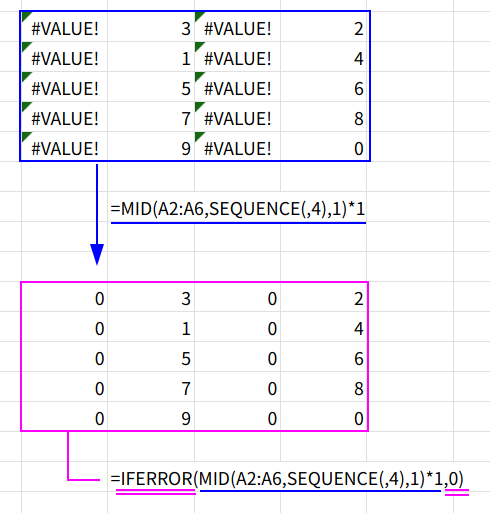
4. IFERROR(..., 0): IFERROR関数が、このエラーだらけの配列をスキャンし、エラーが出ているセルをすべて「0」に置き換えます。{0, 3, 0, 2; 0, 1, 0, 4; ...}
5. SUM(...): 最後に、SUM関数が、この2次元配列に残ったすべての数値を合計し、「45」を導き出します。
メリット: ロジックが「分解→変換→エラー処理→合計」と非常に直感的で、初心者にも理解しやすいです。
デメリット: 「4文字」という前提が崩れると、SEQUENCE(,4)の部分をSEQUENCE(,MAX(LEN(A2:A6)))のように変更する必要があり、少し複雑になります。
アプローチ2：MID + FIND + SEQUENCE（数値指定の検索）
考えかた
アプローチ1と似ていますが、少し発想が異なります。
1文字ずつ分解するのではなく、FIND関数を使って「0から9までの数値が、セルのどこにあるか」を探し出し、その位置の文字をMID関数で抜き出します。
数式と解説
=SUM(IFERROR(MID(A2:A6,FIND(SEQUENCE(,10,0),A2:A6),1),0)*1)
1. SEQUENCE(,10,0): まず、{0,1,2,3,4,5,6,7,8,9}という、検索したい数値の配列を作ります。
2. FIND(..., A2:A6): FIND関数で、A2:A6の各セルに対して、0〜9の各数値がどこにあるかを探します。
結果は、5行10列の巨大な「位置番号」と「#VALUE!エラー」の配列になります。（例: “A3B2″の行は、{エラー,エラー,4,2,エラー,…} となります）
3. MID(A2:A6, ..., 1): MID関数で、見つかった位置番号（4とか2）の文字を抜き出します。エラーの場所は、MID関数もエラーを返します。
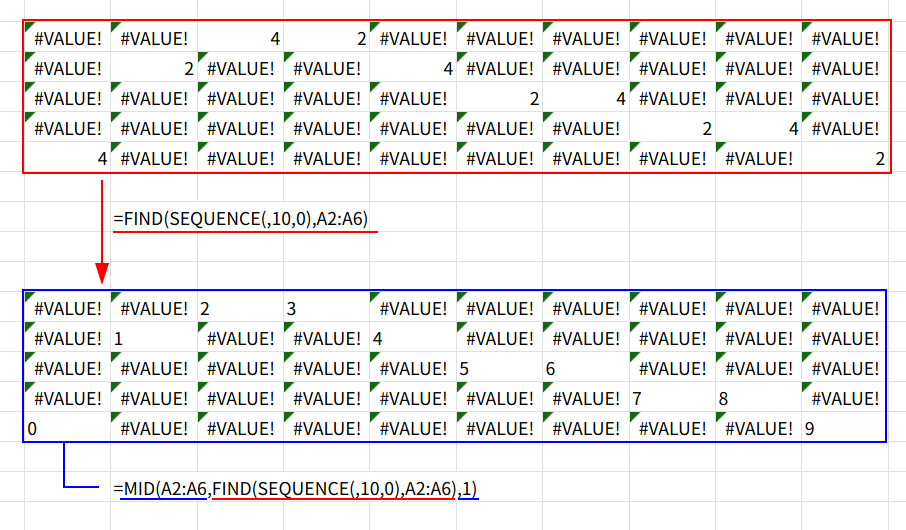
4. IFERROR(..., 0)*1: エラーを0に変換し、抜き出した文字列の数値を、数値に変換します。
5. SUM(...): 最後に合計します。
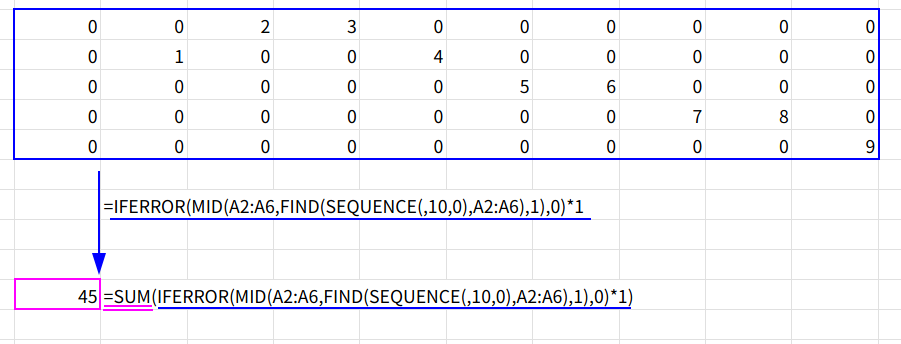
メリット: 「1から5の数値だけ」など、特定の数値だけを抜き出したい場合に、SEQUENCE関数の引数を変えるだけで応用が利きます。
デメリット: FIND関数が同じ文字の2回目以降を見つけられない（例: “A3A3″だと最初の”3″しか見つからない）という弱点があります。（今回は問題ありません）
アプローチ3：RIGHT + LEFT + SEQUENCE（MID禁止の意地）
考えかた
これは、ほぼアプローチ1と同じことを、あえてMID関数を使わずに実現するという、関数パズル愛好家のための数式です（笑）。
数式と解説
=SUM(IF(ISNUMBER(RIGHT(LEFT(A2:A6,SEQUENCE(,4)))*1),RIGHT(LEFT(A2:A6,SEQUENCE(,4))))*1)
1. LEFT(A2:A6,SEQUENCE(,4)): SEQUENCE(,4)（={1,2,3,4}）を使い、各セルの左から1文字、2文字、3文字、4文字を抜き出します。{"A", "A3", "A3B", "A3B2"; ...}
2. RIGHT(...): ステップ1で得られた配列の、各要素の「右端の1文字」を抜き出します。すると、{"A", "3", "B", "2"; ...}となり、アプローチ1のMID関数と全く同じ結果が得られます！
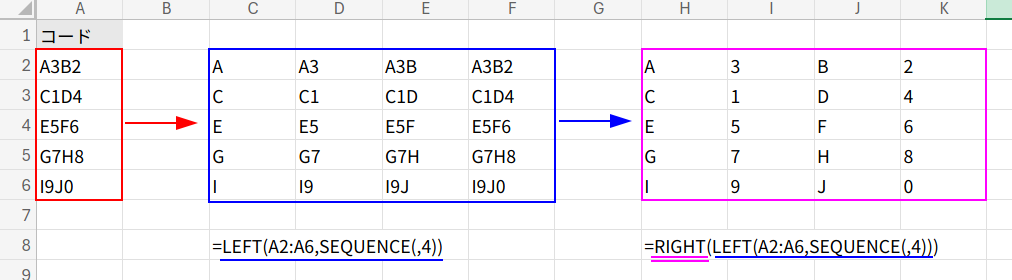
3. IF(ISNUMBER(...*1), ...): あとは、数値に変換できるかどうか（ISNUMBER）を判定し、数値になれるものだけを残して、最後に合計します。
メリット: 「こんな方法でも同じことができる」という、Excelの柔軟性を体感できます。
デメリット: アプローチ1と比べて、数式が明らかに長く、非効率です。実用性はありません！
アプローチ4：TEXTSPLIT + CONCAT + UNICHAR（最新・最強の分離術）
考えかた
ここからは最新の関数を使った、全く異なるアプローチです。
「AからZまでのすべてのアルファベット」を「区切り文字」として指定し、文字列を分割します。すると、残るのは…？
数式と解説
=SUM(TEXTSPLIT(CONCAT(A2:A6),UNICHAR(SEQUENCE(26,,65)),,TRUE)*1)
1. CONCAT(A2:A6): まず、CONCAT関数で、A2:A6のセルをすべて連結し、"A3B2C1D4E5F6G7H8I9J0"という一本の巨大な文字列にします。
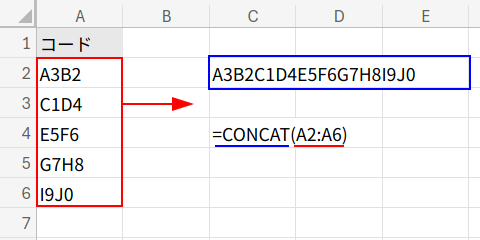
2. UNICHAR(SEQUENCE(26,,65)): ここが最大の魔法！SEQUENCE(26,,65)で、65から90までの26個の連番を作ります。
これは、PCの文字コード（Unicode/ASCII）で「A」から「Z」に対応する番号です。
それをUNICHAR関数に通すことで、{"A";"B";"C";...;"Z"}という、アルファベット全26文字の配列を生成します。
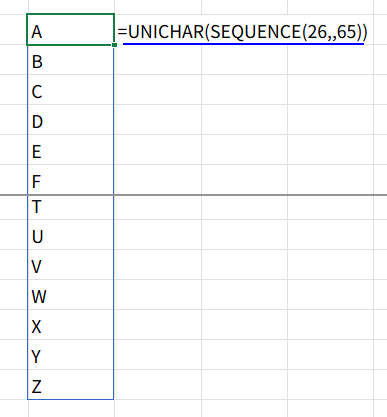
3. TEXTSPLIT(..., ..., ,TRUE): TEXTSPLIT関数を使い、ステップ1の巨大な文字列を、ステップ2の「アルファベット全26文字の配列」を区切り文字として分割します。
4番目の引数TRUE（ignore_empty）で、アルファベットが連続した部分（”AB”など）で発生する空白セルを無視します。
4. 結果として、{"3";"2";"1";"4";...}という、数値だけが抜き出された配列が返されます！
5. ...*1 と SUM(...): 最後に、文字列の数値を数値に変換し、合計します。
メリット: 非常に強力で、文字数が4文字でなくても、アルファベットが何個続いても対応できる、高い汎用性を持っています。
デメリット: TEXTSPLITなどの最新関数が使えるMicrosoft 365環境が必須です。
アプローチ5：FILTER + MID + CONCAT
考えかた
アプローチ4と似ていますが、今度は「アルファベットを区切り文字にする」のではなく、「1文字ずつに分解し、数値になれるものだけをFILTER関数で選び出す」というロジックです。
数式と解説
=SUM(FILTER(MID(CONCAT(A2:A6),SEQUENCE(20),1)*1,ISNUMBER(MID(CONCAT(A2:A6),SEQUENCE(20),1)*1)))
1. CONCAT(A2:A6): “A3B2C1D4…” という巨大な文字列を作ります（今回は5セル×4文字=20文字）。
2. MID(..., SEQUENCE(20), 1): SEQUENCE関数で1から20までの連番を生成し、MID関数で文字列を1文字ずつ、{"A";"3";"B";"2";...}という縦一列の配列に分解します。
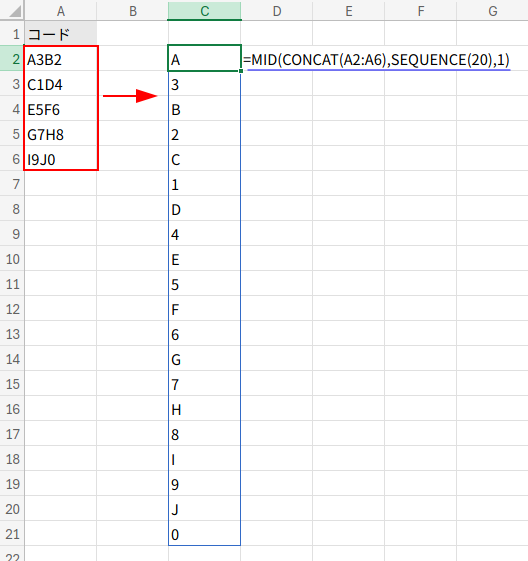
3. ... * 1: この配列を数値に変換しようと試み、{#VALUE!;"3";#VALUE!;"2";...}という、数値とエラーが混在した配列を作ります。（これがFILTERの対象配列）
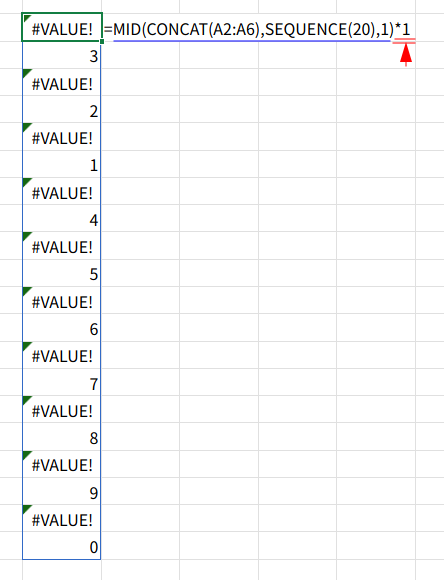
4. ISNUMBER(...): ステップ3の配列が数値かどうかを判定し、{FALSE;TRUE;FALSE;TRUE;...}というTRUE/FALSEの配列を作ります。（これがFILTERの条件）
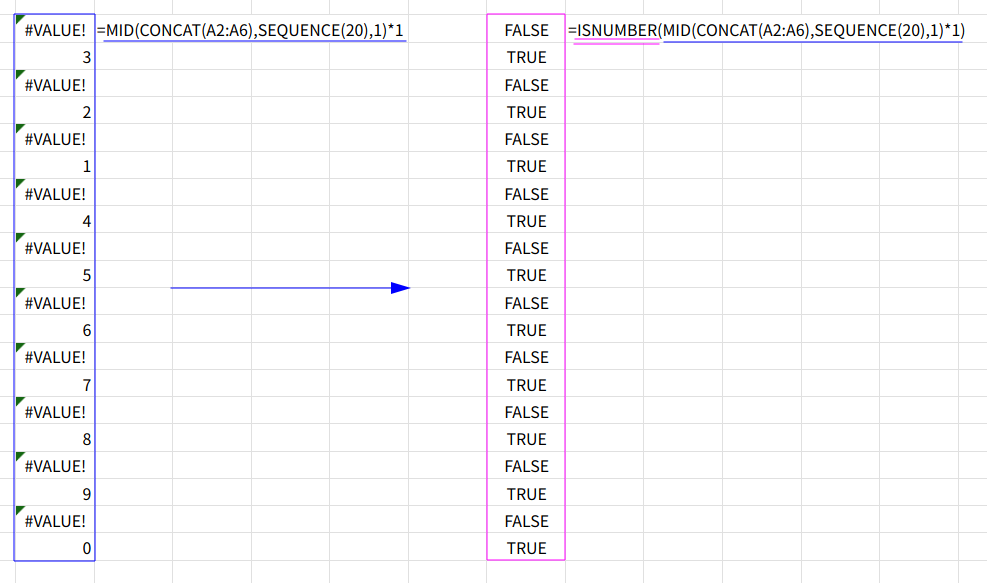
5. FILTER(...): FILTER関数が、ステップ3の配列を、ステップ4の条件（TRUEのものだけ）で絞り込みます。結果、{3;2;1;4;...}という、数値だけの配列が残ります。
6. SUM(...): 最後に、この絞り込まれた数値を合計します。
メリット: 「エラーを0に変える」のではなく、「エラーを最初から除外する」という、より純粋なロジックです。
デメリット: 数式が長く、MID(CONCAT(...))という同じ処理を2回も書いているため、少し非効率です。
アプローチ6：LOOKUP + UNICODE + MOD（文字コードで判定）
考えかた
これは、今回最もマニアックで、しかし非常に巧妙な関数パズルです。
UNICODE関数で各文字の「文字コード」を調べ、LOOKUP関数を使って「数値の文字コード」だけを「0〜9の数値」に変換し、アルファベットは「0」に変換します。
数式と解説
=SUM(LOOKUP(UNICODE(MID(CONCAT(A2:A6),SEQUENCE(20),1)),SEQUENCE(11,,48),MOD(SEQUENCE(11,,0),10)))
1. MID(CONCAT(A2:A6),SEQUENCE(20),1): アプローチ5と同様に、{"A";"3";"B";"2";...}という全文字の配列を作ります。
2. UNICODE(...): 各文字の文字コードを調べます。{65; 51; 66; 50; ...}
（”A”=65, “B”=66, “0”=48, “1”=49, “2”=50, “3”=51 …）
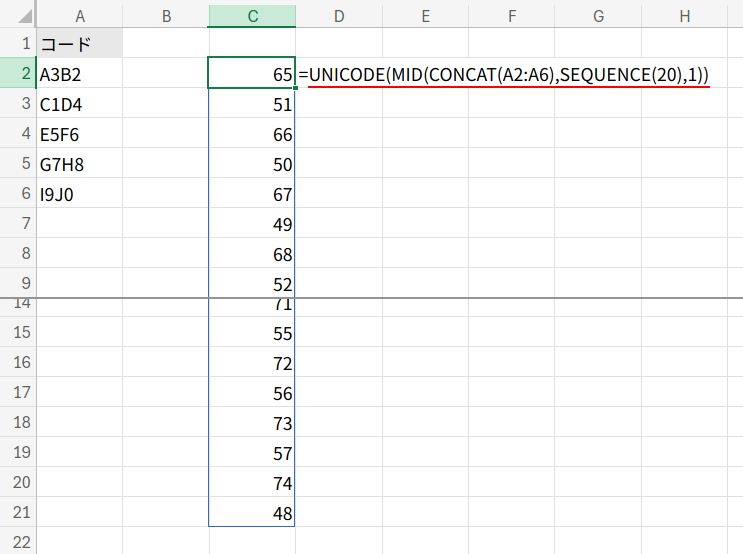
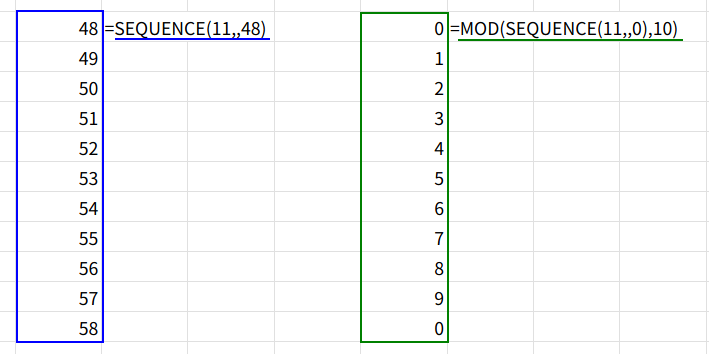
3. SEQUENCE(11,,48): LOOKUPの「検索範囲」として、{48;49;50;51;52;53;54;55;56;57;58}という配列を作ります。（これは”0″から”9″の文字コードと、それより1つ大きい数です）
4. MOD(SEQUENCE(11,,0),10): LOOKUPの「戻り値の範囲」として、{0;1;2;3;4;5;6;7;8;9;0}という配列を作ります。
5. LOOKUP(...): ここが最大の魔法！LOOKUP（近似一致）が、ステップ2の文字コードを、ステップ3の検索範囲で探します。
・「65 (A)」を探すと、範囲内の最大値(58)より大きいため、戻り値配列の最後の値「0」が返されます。
・「51 (3)」を探すと、51以下の最大値は51（4番目）なので、戻り値配列の4番目「3」が返されます。
・「50 (2)」を探すと、50以下の最大値は50（3番目）なので、戻り値配列の3番目「2」が返されます。
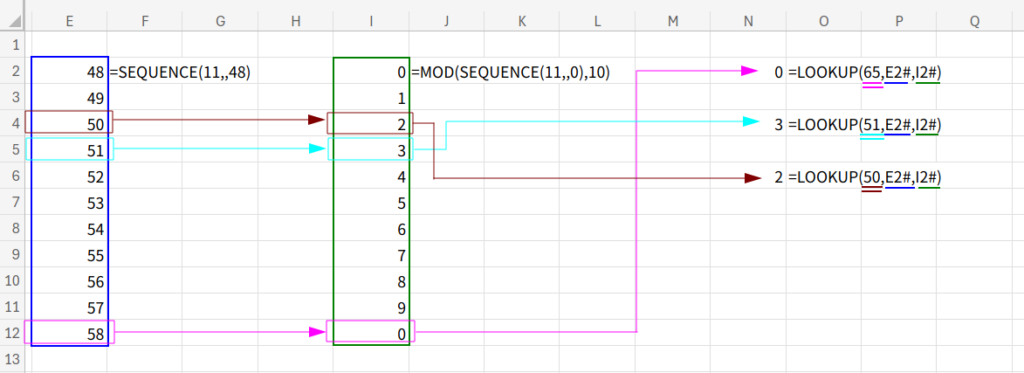
6. 結果として、{0;3;0;2;0;1;...}という、数値だけが正しく変換された配列が得られます！
7. SUM(...): 最後に、これを合計します。
メリット: IFERRORもISNUMBERも使わずに、数値変換とエラー処理を同時に行っている、非常に高度で美しいロジックです。
デメリット: 難解すぎます（笑）。文字コードの知識とLOOKUPの特殊な挙動の両方を理解していないと、解読はほぼ不可能です。
まとめ：文字列操作は、ロジックの宝庫だ！
たった一つのシンプルなゴールに対して、これほどまでに多様なアプローチが存在することに、楽しんでいただけたのではないでしょうか。
実務で使うなら、アプローチ1のIFERROR(MID(…)*1,0)が最もバランスが取れていますし、最新のExcelが使えるならアプローチ4のTEXTSPLITが最強かもしれません。
しかし、他の関数パズルたちも、決して無駄ではありません。
FINDとMIDの連携、LEFTとRIGHTによる分解、そしてUNICODEとLOOKUPを使った暗号解読のようなテクニック…。
これらの知識は、あなたの「Excel問題解決能力」を確実に引き上げてくれます。
今回の関数パズルが、皆さんのExcelへの知的好奇心をさらに深めるきっかけになれば、これほど嬉しいことはありません。
