- はじめに:祝・100記事!記念すべきテーマは「偶数判定」だ!
- 準備:挑戦者となる数値たち
- 9つのアプローチで、「偶数」を攻略せよ!
- まとめ:100回目も、やっぱりExcelは面白い!
はじめに:祝・100記事!記念すべきテーマは「偶数判定」だ!
「Excelで暇つぶし」をご覧いただき、本当にありがとうございます!
おかげさまで、なんと今回で、記念すべき100記事目を迎えることができました!
これもひとえに、読んでくださる皆様の知的好奇心と、Excelへの愛のおかげです。
さて、そんな100記事目の節目にふさわしいテーマは…?
「LAMBDA」?「Power Query」?いえいえ、違います。
今回のテーマは、「偶数判定」です!
「え、偶数判定?それって、MOD(数値,2)=0 で終わりじゃない?」
そう思ったあなた、その通り!でも、もしMOD関数が使えなかったら?もし、関数を一切使わずに「演算子だけ」で判定しろと言われたら…?
今回の記事は、この「2で割り切れる数」というシンプルなゴールに対して、実に9種類もの異なるアプローチで挑む、知的な関数パズルです。
この偶数判定のロジックは、条件付き書式で『1行おきに背景色を変える(シマシマにする)』時にもそのまま使えます!
【ルール】
1. 「一度使った関数は二度と使わない」という縛りプレイでいきます!
2. 対象は「整数」のみとします。小数を含めた偶数判定は非常に複雑になるため、今回はロジックの面白さを最優先します!
3. エラー処理なども考慮せず、純粋なロジックを楽しみましょう!
この冒険を通して、あなたの「Excel脳」と「数学脳」が、さらに鍛えられること間違いなしです!
本記事では、無料のWeb版Excelを使用して検証および画像の作成を行っています。Windowsはもちろん、MacやLinuxの方もブラウザさえあれば挑戦できます!
準備:挑戦者となる数値たち
まずは、準備から。まっさらなシートのA1セルを起点に、以下の8行1列のリストを作成してください。
下の数式をA1セルに貼り付けます。
={"偶数判定";-13;-4;-1;0;2;17;102}
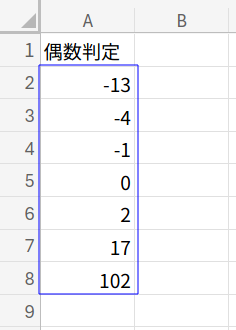
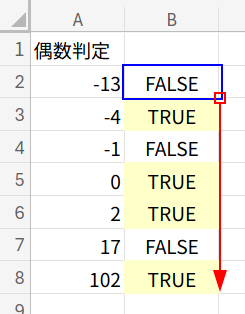
負の数、0、正の奇数、正の偶数…と、判定しがいのあるメンバーが揃いましたね。
ゴールは、任意の列に数式を入力(フィルコピー)し、A列が偶数なら「TRUE」、奇数なら「FALSE」と正しく表示させることです。
9つのアプローチで、「偶数」を攻略せよ!
今回は、数式を入力しフィルコピーする方法を基本に、おまけとして「スピル版」の数式も紹介していきますよ!
関数の詳細な仕様については、Microsoft公式のヘルプも参考にしてください。
アプローチ1:ISEVEN – 偶数判定のために生まれた関数
考えかた
まずは、その名の通り「偶数ですか?(Is Even?)」と尋ねるための、専用関数から参りましょう。
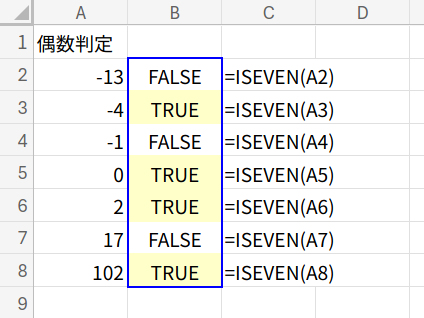
数式と解説(フィルコピー版)
=ISEVEN(A2)
・ISEVEN(数値): 引数に指定した数値が偶数ならTRUE、奇数ならFALSEを返します。0も偶数として扱われます。これ以上ないほどシンプルですね!
スピルさせる場合
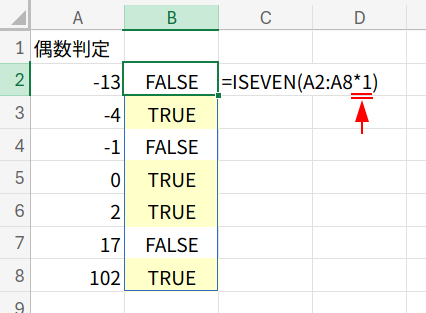
=ISEVEN(A2:A8*1)
=ISEVEN(A2:A8)
「あれ? =ISEVEN(A2:A8) じゃダメなの?」
良い質問です!
実は、=ISEVEN(A2:A8) と入力すると、#VALUE! エラーになってしまいます。
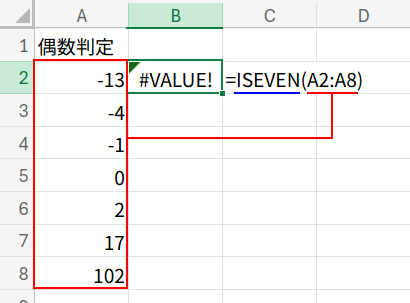
ISTEXTやISBLANKのような情報系関数は配列をそのまま扱えるのですが、不思議なことにISEVENやISODDは、配列を直接引数に取ることを想定されていないようです。(これは、Excelの古いバージョンとの互換性を保つための仕様かもしれませんね。)
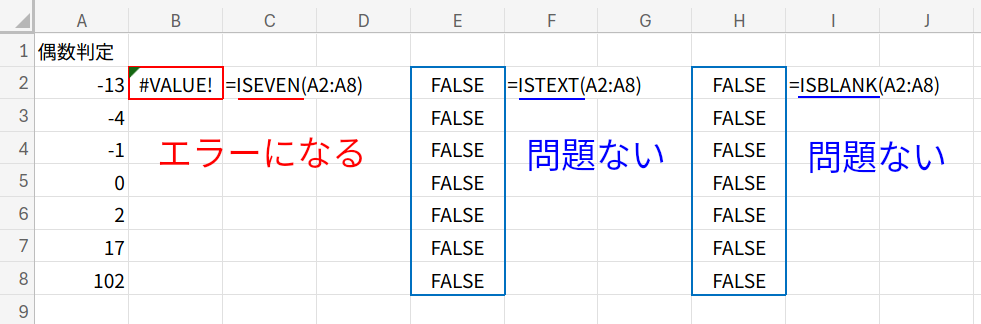
そこで、A2:A8*1という計算を挟むことで、Excelに「A2:A8の各要素に1を掛けた、新しい配列」を強制的に認識させ、その結果の配列の各要素に対してISEVENを適用させる、というテクニックを使っています。
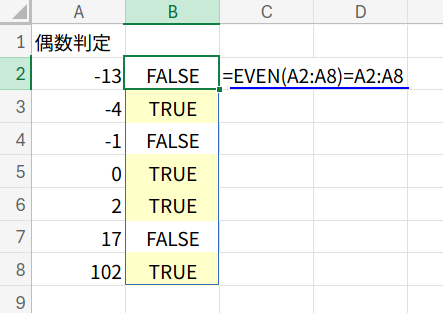
アプローチ2:EVEN – 偶数に切り上げる関数
考えかた
次に、数値を最も近い偶数に(絶対値が増える方向に)切り上げるEVEN関数を使います。
「切り上げ後の数値」と「元の数値」が同じなら、その数は元から偶数だった、と言えますよね?
数式と解説(フィルコピー版)
=EVEN(A2)=A2
・EVEN(A2): 例えばA2が「-13」なら「-14」に、「-4」なら「-4」に、「17」なら「18」に切り上げます。
・...=A2: この結果と、元のA2の値を比較します。
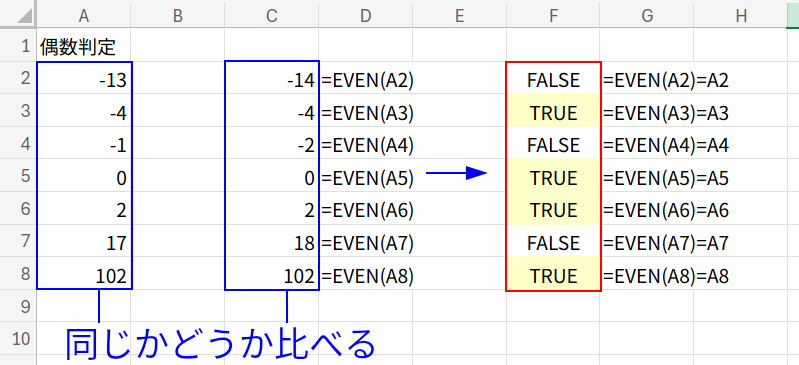
EVEN(-13)は-14 → -14 = -13 は FALSEEVEN(-4)は-4 → -4 = -4 は TRUEEVEN(17)は18 → 18 = 17 は FALSE
見事に判定できていますね!
スピルさせる場合
=EVEN(A2:A8)=A2:A8
ISEVENと違い、こちらはなぜか素直にスピルしてくれます。
Excelの謎は深まるばかりです…笑
アプローチ3:MOD – 汎用性の王様
考えかた
実務での汎用性を考えれば、この関数が最強でしょう。
「2で割った余り」を計算する、MOD関数です。
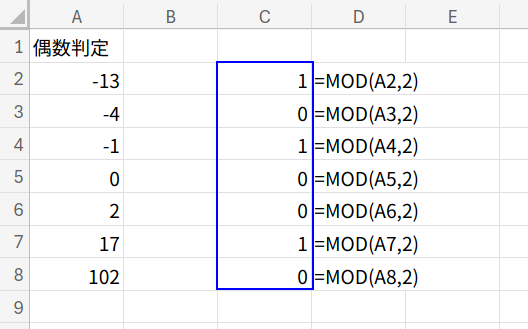
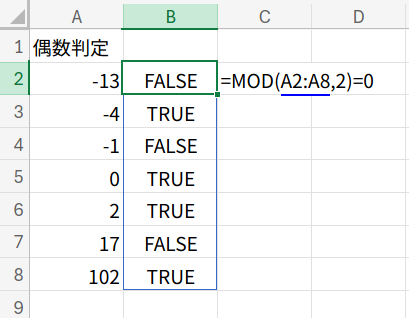
数式と解説(フィルコピー版)
=MOD(A2,2)=0
・MOD(A2,2): A2の数値を2で割った余りを計算します。偶数なら「0」、奇数なら「1」(負の奇数の場合も「1」)が返ります。
・...=0: その結果が「0」かどうかを判定します。これで、正しく偶数判定ができます。
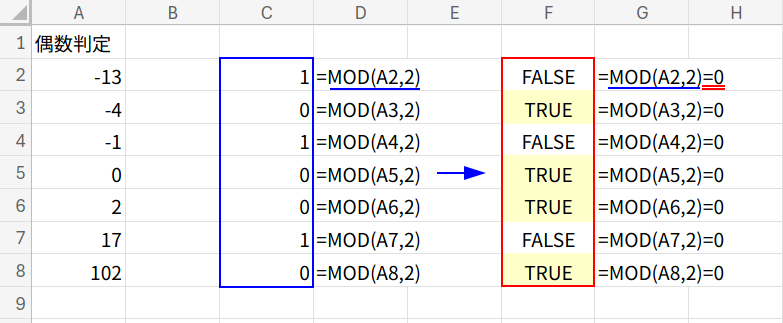
3の倍数なら=MOD(A2,3)=0など、応用が利くのが素晴らしいですね。
スピルさせる場合
=MOD(A2:A8,2)=0
アプローチ4:INT – 割り算と切り捨ての比較
考えかた
次は、数値の切り捨てを行うINT関数を使います。
もし、「数を2で割ったもの」と、「数を2で割って小数点以下を切り捨てたもの」が同じなら、その数は元から割り切れていた(=偶数)はずだ、というロジックです。
数式と解説(フィルコピー版)
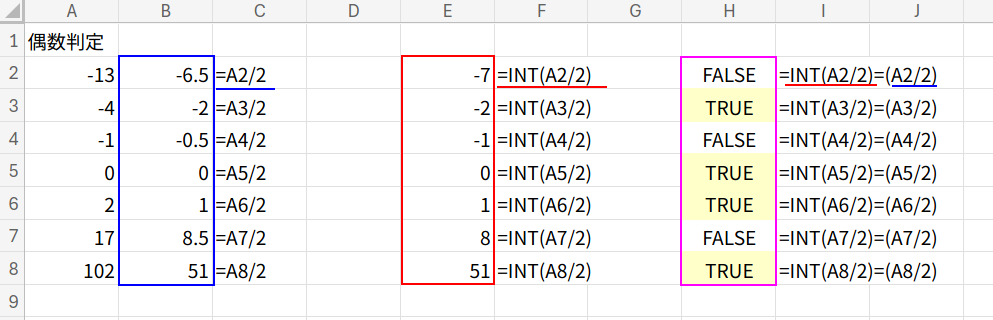
=INT(A2/2)=(A2/2)
・A2/2: まず、数を2で割ります。(例: -13 → -6.5, -4 → -2, 17 → 8.5)
・INT(A2/2): それをINT関数で切り捨てます。(例: -6.5 → -7, -2 → -2, 8.5 → 8)
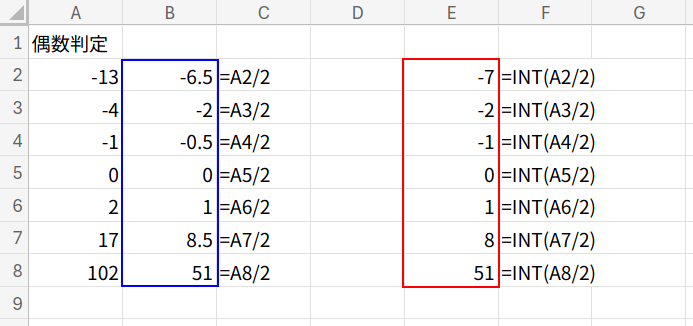
・... = ...: この2つを比較します。
- -6.5 = -7 は FALSE
- -2 = -2 は TRUE
- 8.5 = 8 は FALSE
このロジックは、QUOTIENT(A2,2)やTRUNC(A2/2)でも同じことができますよ!
スピルさせる場合
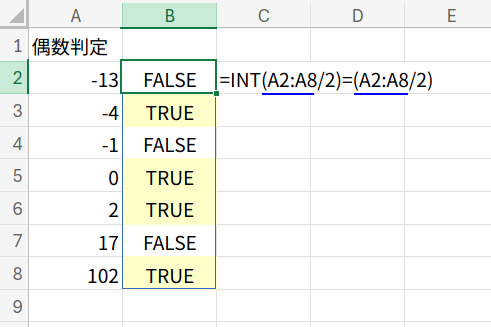
=INT(A2:A8/2)=(A2:A8/2)
アプローチ5:BITAND – 2進数の世界へようこそ
考えかた
ここからはマニアックな領域です。コンピュータの内部、2進数の世界で考えてみましょう。
2進数では、すべての偶数は「一番下の桁(ビット)が0」、すべての奇数は「一番下の桁が1」になります。この性質を利用します。
数式と解説(フィルコピー版)
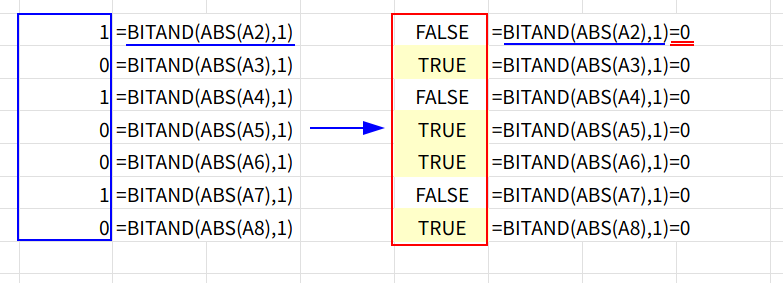
=BITAND(ABS(A2),1)=0
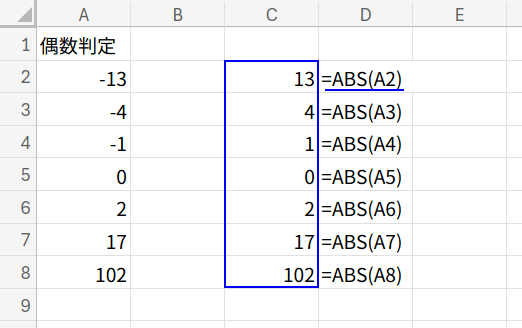
・ABS(A2): BITAND関数は負の数を指定すると#NUM!エラーになる(つまり、負の数は扱えない)ので、まずABS関数で絶対値(正の数)にします。
・BITAND(..., 1): BITAND関数は、2つの数値を2進数で比較し、両方のビットが1の桁だけを1として返します(ビット単位の論理積)。

・...=0: 0なら偶数(TRUE)、1なら奇数(FALSE)となります。
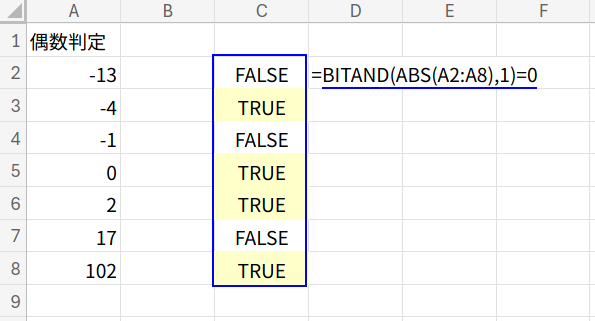
スピルさせる場合
=BITAND(ABS(A2:A8),1)=0
アプローチ6:XOR + MUNIT – 行列と論理演算の融合
考えかた
これは、もはや芸術的な関数パズルです。
MUNIT関数で単位行列を作り、XOR(排他的論理和)関数の「TRUEが奇数個ならTRUE」という性質を悪用(?)します。
数式と解説(フィルコピー版)
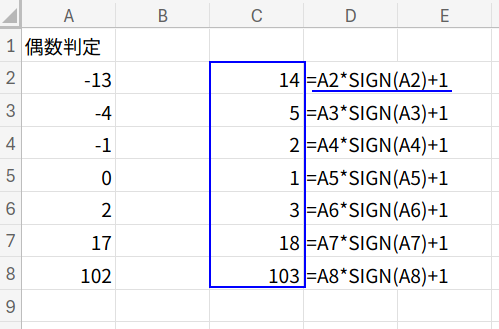
=XOR(MUNIT(A2*SIGN(A2)+1))
1. A2*SIGN(A2)+1: SIGN関数は符号(1, -1, 0)を返します。
A2*SIGN(A2)はABS(A2)とほぼ同じで、数値の絶対値を計算します。それに1を足します。(例: -13 → 14, -4 → 5)
2. MUNIT(...): MUNIT関数で、ステップ1の数値をサイズとする単位行列(対角線が1で他は0)を作ります。
下の画像は=MINIT(14)の場合。

3. XOR(...): XOR(排他的論理和)関数は、範囲内のTRUE(または1)の個数が「奇数」ならTRUEを、「偶数」ならFALSEを返します。
単位行列に含まれる「1」の個数は、そのサイズ(N x N)と同じN個です。つまり…
・-13(奇数) → XOR(MUNIT(14)) → 1が14個(偶数個)→ FALSE
・-4(偶数) → XOR(MUNIT(5)) → 1が5個(奇数個)→ TRUE
これは見事な偶数判定式です!
スピルさせる場合
この数式は、XOR関数の特性上、スピルに対応できません。
アプローチ7:DEC2BIN + RIGHT – 2進数文字列操作
考えかた
アプローチ5と発想は同じですが、今度は2進数を「文字列」として扱います。
10進数を2進数文字列に変換し、その「右端の1文字」が”0″かどうかを判定します。
数式と解説(フィルコピー版)
=RIGHT(DEC2BIN(A2))*1=0
・DEC2BIN(A2): DEC2BIN関数で、A2の数値を2進数の文字列に変換します。
この関数には「-512から511まで」という厄介な制限があります。これは、Excelが内部的に10ビットの2の補数表現でこの計算を行うためです。範囲外の数値(例: 512,-513)は #NUM! エラーになります。
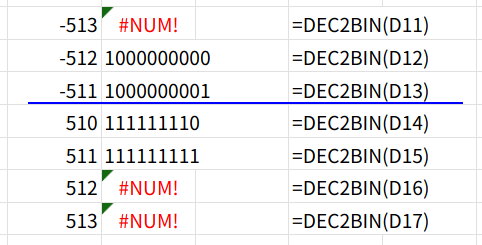
・RIGHT(...): その文字列の右端の1文字を抜き出します。(偶数は”0″, 奇数は”1″)
・...*1=0: 抜き出した文字を*1で数値に変換し、「0」かどうかを判定します。
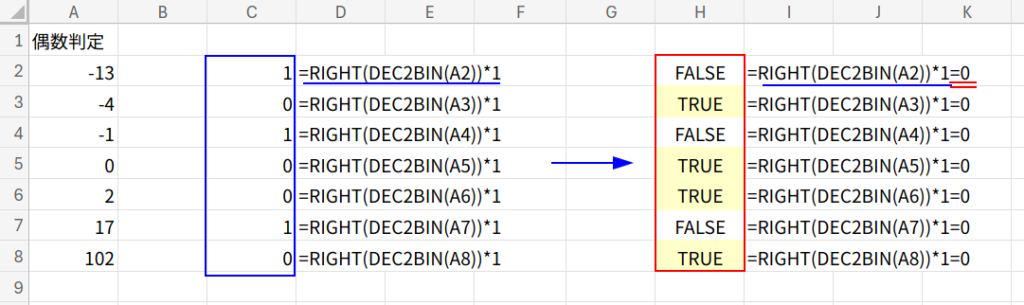
スピルさせる場合
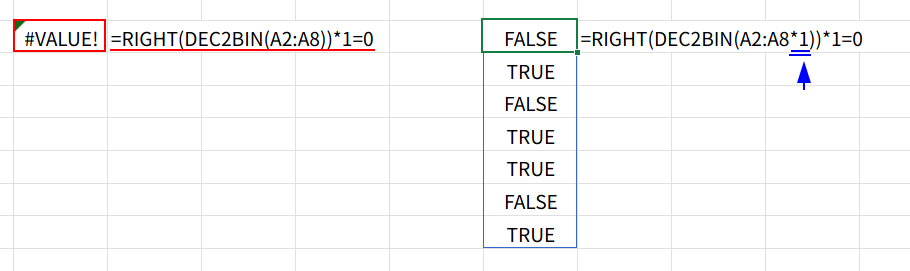
=RIGHT(DEC2BIN(A2:A8*1))*1=0
=RIGHT(DEC2BIN(A2:A8))*1=0
これもISEVENと同様に、*1で配列を強制的に認識させる必要がありますね。
アプローチ8:COS + PI – 三角関数の悪用
考えかた
いよいよ何でもありの世界です(笑)。コサインカーブの性質を利用します。
COS(π*n)は、nが整数なら、nが偶数の時は「1」、奇数の時は「-1」を返します。この性質を使います!
数式と解説(フィルコピー版)
=COS(PI()*(A2^2)^(1/2))=1
・(A2^2)^(1/2): ABS(A2)の、数学的な遠回り表現です。2乗して平方根を取ることで、絶対値にしています。関数縛りルールにより、ABS関数を再登場させないための工夫ですね。
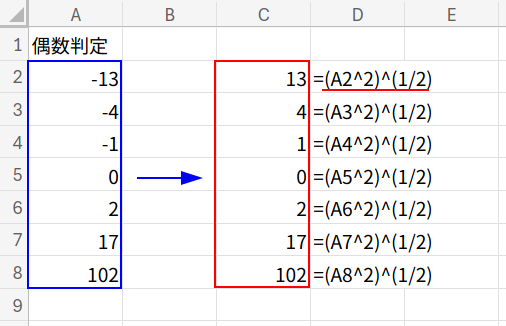
・PI()*(...): 絶対値に円周率πを掛けます。
・COS(...): コサインを計算します。
COS(13*π)→ -1COS(4*π)→ 1COS(0)→ 1
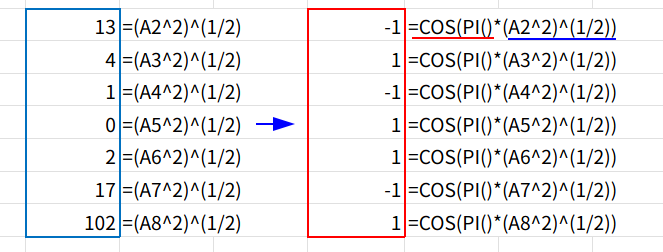
・...=1: 結果が「1」かどうかを判定します。見事に偶数(0を含む)だけがTRUEになりますね!
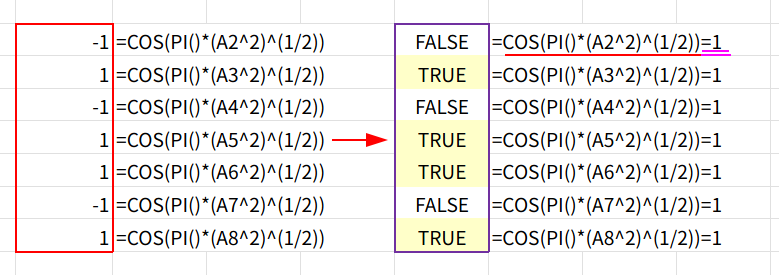
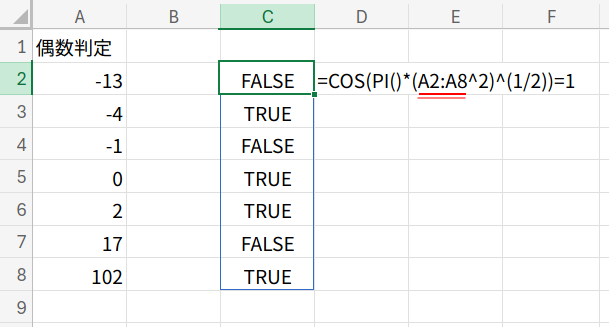
スピルさせる場合
=COS(PI()*(A2:A8^2)^(1/2))=1
=COS(PI()) この数式は以下の記事でちょこっと紹介しています!
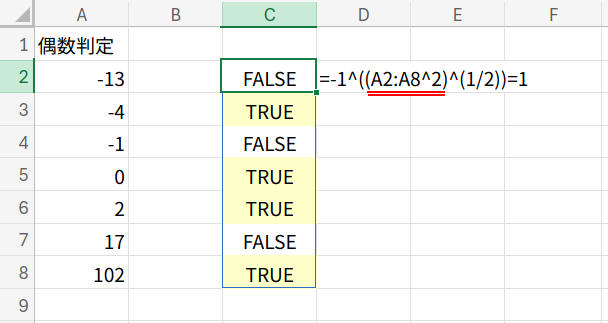
アプローチ9:演算子のみ! – 関数からの卒業
考えかた
最後は、この記事のクライマックス!
関数を一切使わずに、「演算子だけ」で偶数判定に挑みます。
アプローチ8のロジック、COS(π*n)は「-1のn乗」と全く同じ動きをします。
数式と解説(フィルコピー版)
=-1^((A2^2)^(1/2))=1
・(A2^2)^(1/2): ABS(A2)(数値の絶対値)を、演算子だけで表現しています。

・-1^(...): 「-1」を、絶対値の数だけべき乗します。ここで、中学数学を思い出してみましょう!
- (-1) × (-1) = 1 (マイナス × マイナス = プラス)
- (-1) × (-1) × (-1) = -1 (マイナス × マイナス × マイナス = マイナス)
つまり、マイナス1は、偶数回掛ければ「1」に、奇数回掛ければ「-1」になるのです!
-1^13→ -1 (奇数)-1^4→ 1 (偶数)-1^0→ 1 (偶数)
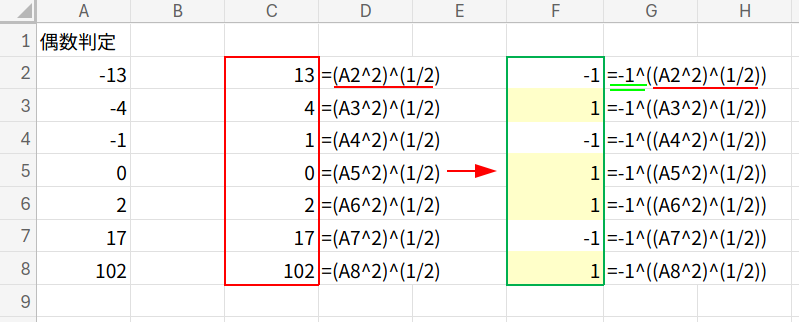
・...=1: 結果が「1」かどうかを判定します。関数を一切使わずに、偶数判定が完成しました!
これぞExcel脳、数学脳を鍛える最高の練習問題ですね!

スピルさせる場合
=-1^((A2:A8^2)^(1/2))=1
まとめ:100回目も、やっぱりExcelは面白い!
たった一つのシンプルなゴールに対して、これほどまでに多様で、奇妙で、そして美しいアプローチが存在することに、Excelの底知れぬ奥深さを感じていただけたのではないでしょうか。
実務で使うなら、アプローチ3のMOD関数(=MOD(A2,2)=0)が、誰にとっても分かりやすく、汎用性も高いため最強です。
しかし、アプローチ5の2進数の考え方や、アプローチ9の演算子だけの解法は、Excelの本質的な部分や、その背景にある数学の美しさを私たちに教えてくれます。
「Excelで暇つぶし」は、これからも、こんな風に「どうでもいい」けれど、皆さんの知的好奇心を刺激するような、たくさんのコンテンツでExcelの楽しさをお届けしていきます。
100記事までお付き合いいただき、本当にありがとうございました!
そして、これからも「Excelで暇つぶし」を、どうぞよろしくお願いいたします!