はじめに：INT関数、実は奥が深いんです。
「数値を整数にしたい！」
そんな時、真っ先に思い浮かぶのは INT関数 ですよね。
でも、このINT関数、実は「ただ小数点以下を切り落としている」わけではないことをご存知でしょうか？
特に「負の数（マイナス）」の時、その性格が露わになります。
例えば、「-0.2」を整数にするとどうなるでしょう？
- TRUNC関数 / ROUNDDOWN関数： 「0」になります。（0に向かって切り捨てる）
- INT関数： 「-1」になります。（より小さい値に向かって切り捨てる）
そう、INT関数は常に「マイナスの無限大方向」に向かって数値を丸めるのです。
今回のテーマは、「INT関数なしで、この独特な挙動を完全再現する」こと！
実務で役立つ知識から、明日誰かに言いたくなるマニアックな関数パズルまで、5つの方法でこの難題に挑みます。
本記事では、無料のWeb版Excelを使用して検証および画像の作成を行っています。Windowsはもちろん、MacやLinuxの方もブラウザさえあれば挑戦できます！
ステップ1：冒険の準備 – テストデータ
まずは、A1セルを起点に以下のテストデータを用意してください。
={"数値";-9.8;-7;-4;-0.2;0;0.9;3.4;6;11}
負の数、0、正の数、小数が入り混じったこのリスト。INT関数を通すと、以下のようになります。
正解（ゴール）： {-10; -7; -4; -1; 0; 0; 3; 6; 11}
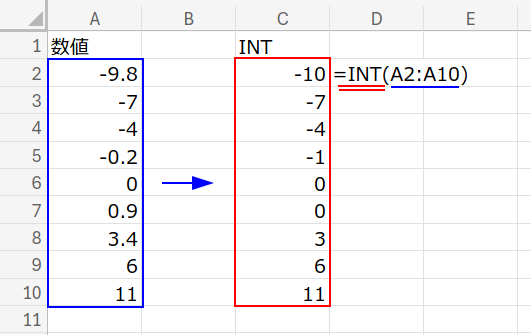
さあ、INT関数を使わずに、この答えを導き出せるでしょうか？
5つのアプローチで、「INT」を再現せよ！
今回はすべての数式をD2セルに入力し、スピル機能を使って一気に結果を表示させます。
1. FLOOR.MATH関数 – オプションで自在に制御
考えかた
まずは一番スマートな方法から。
Excel 2013から登場した FLOOR.MATH 関数を使います。
これは、数値を指定した倍数（基準値）に切り下げる関数です。
数式と解説
=FLOOR.MATH(A2:A10,1)
FLOOR.MATH(数値, 基準値, [モード])
この関数は、指定した「基準値」の倍数の中で、元の数値より「小さい」最大の値を返します。
基準値を「1」に設定することで、「1の倍数（つまり整数）」かつ「元の数より小さい数」を求めることになり、これはINT関数の定義そのものです！
※ちなみに、似た関数にFLOORがありますが、これは負の数の処理でエラーが出たり挙動が違ったりするので、現代ではFLOOR.MATHが推奨です。
2. ROUNDDOWN関数 – 余計なものを引いて調整
考えかた
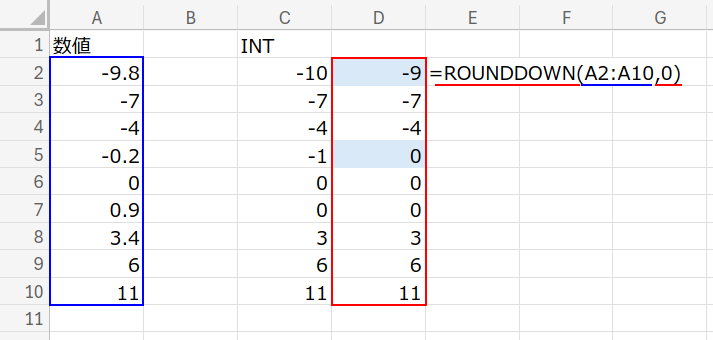
次は王道の切り捨て関数 ROUNDDOWN です。
しかし、これは「0方向」に切り捨てるため、負の数の時だけ計算が合いません（-9.8が-9になってしまう）。
そこで、「負の数」かつ「小数がある」時だけ、さらに「1」を引いてあげる調整を行います。
TRUNC関数やQUOTIENT関数を使用する場合も、全く同じロジックです。
数式と解説
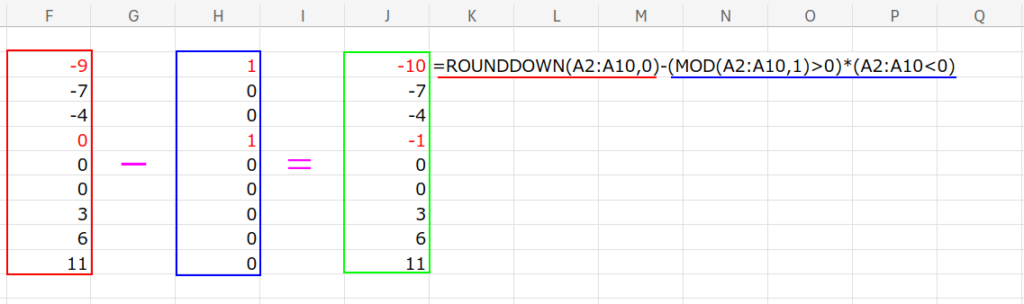
=ROUNDDOWN(A2:A10,0)-(MOD(A2:A10,1)>0)*(A2:A10<0)
1. ROUNDDOWN(A2:A10, 0): まずは普通に小数点を切り捨てます。
正の数はこれでOKですが、負の数は足りません（-9.8 → -9）。
2. (MOD(A2:A10, 1)>0): 小数部分があるかをチェックします。割り切れる整数なら調整不要だからです。
3. (A2:A10<0): 負の数かどうかをチェックします。
4. ... - (...): 「小数あり」かつ「負の数」の場合のみ、条件式が 1 * 1 = 1 となり、ROUNDDOWNの結果から「1」が引かれます。
（例：-9 – 1 = -10）これでINTと同じになります！
3. MOD関数 – 数学的な美しさ
考えかた
「元の数」から「はみ出た部分（余り）」を引けば、きれいに整数になるはずですよね？
実は、Excelの MOD 関数は、負の数に対して非常に数学的に正しい「余り」を返してくれます。
数式と解説
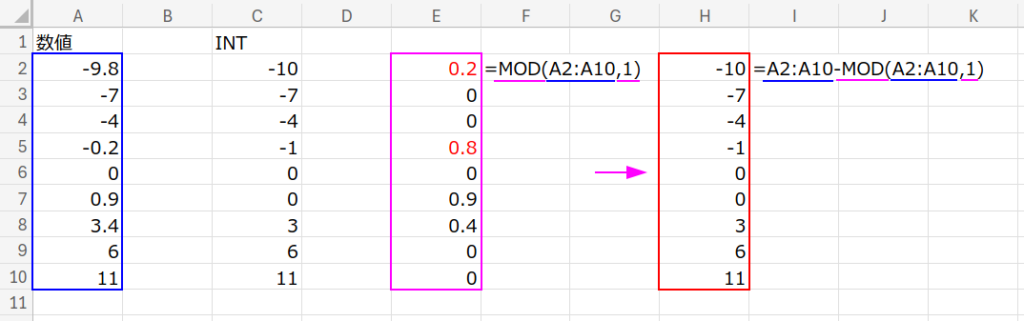
=A2:A10-MOD(A2:A10,1)
これだけでいいんです！驚きですよね。
ポイントは、MOD関数の「除数（割る数）と同じ符号の余りを返す」という性質です。
・正の数（3.4）の場合：MOD(3.4, 1) は「0.4」です。3.4 - 0.4 = 3 （正解！）
・負の数（-9.8）の場合：
ここが面白い！ MOD(-9.8, 1) は、実は「0.2」になります。（-0.8ではありません！）
なぜなら、-10 + 0.2 = -9.8 だからです。
式に戻ると、-9.8 - 0.2 = -10 （正解！）
算数が苦手な人には魔法に見えますが、数学的にはこれが最も美しい解法です。
4. EVEN関数 – 偶数を使って整数を作る！？
考えかた
「偶数に切り上げる」という全く用途の違う EVEN 関数を使っても、INTを再現できます。発想の転換です。
数式と解説
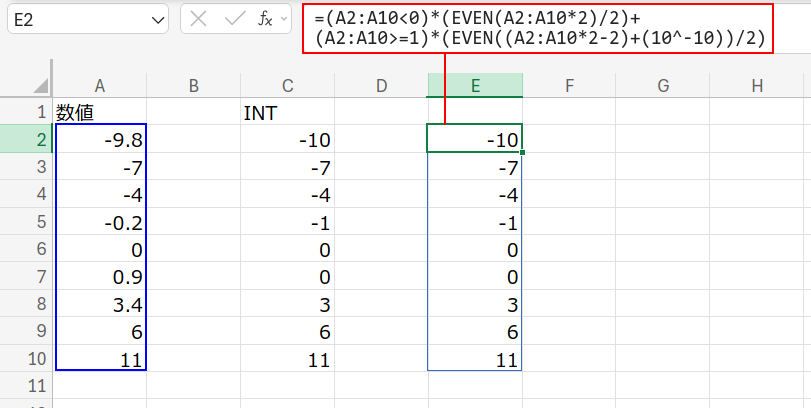
=(A2:A10<0)*(EVEN(A2:A10*2)/2)+(A2:A10>=1)*(EVEN((A2:A10*2-2)+(10^-10))/2)
この数式は「負の数」と「正の数」で処理を分けています。
【負の数のロジック】 EVEN(数値*2)/2
例えば「-0.2」を考えます。
- 2倍する：
-0.4 - EVENで偶数に切り上げ（負の方向へ）：
-2 - 2で割る：
-1（INTと同じ！）
【正の数のロジック】 EVEN(数値*2 - 2 + 微小値)/2
例えば「3.4」を考えます。
- 2倍して2を引く：
6.8 - 2 = 4.8 - EVENで偶数に切り上げ（正の方向へ）：
6 - 2で割る：
3（INTと同じ！）
【計算誤差に注意！】
数式の中にある 10^-10 は、Excelの計算誤差対策です。
また、この方法は面白いですが、Excelの仕様上、数値が大きくなりすぎると計算精度が落ちたり、EVEN関数の挙動が不安定になる可能性があります。
あくまで「パズル」として楽しむのが良さそうです。
5. LOOKUP + SUBTOTAL – 全整数リストを作る力技
考えかた
最後は、「データ範囲をカバーする整数の連番（定規のようなもの）」をメモリ上に作り出し、LOOKUP関数でそこから「近似一致（以下の最大値）」を探し出すという、ダイナミックな手法です。
数式
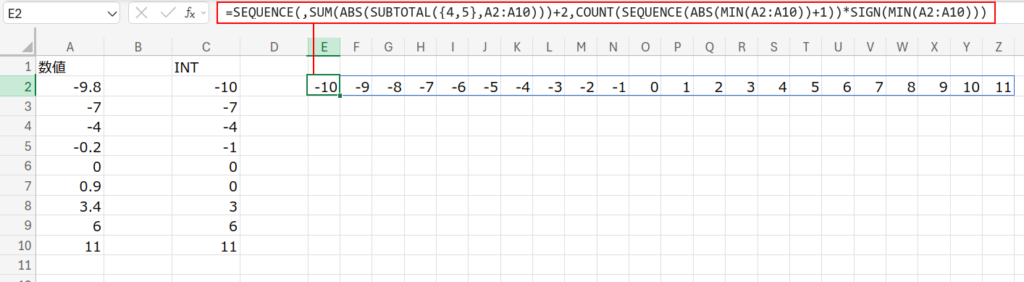
=LOOKUP(A2:A10,SEQUENCE(,SUM(ABS(SUBTOTAL({4,5},A2:A10)))+2,COUNT(SEQUENCE(ABS(MIN(A2:A10))+1))*SIGN(MIN(A2:A10))))
長い！何をやっているんでしょうか？分解しましょう。
この数式は、LOOKUP(検索値, 検索範囲) という、第3引数（対応範囲）を省略した「配列形式」の書き方を使っています。
この形式では、「検索範囲」に入っている値そのものが答えとして返ってきます。
① 第1引数：検索値 A2:A10
ここはシンプルです。切り捨て（整数化）したい元のデータ配列です。 {-9.8; -7; -4; ...; 11} などの数値が入っています。
② 第2引数：検索範囲（兼 戻り値）
ここがこの数式の心臓部です！
SEQUENCE関数を使って、データの最小値から最大値までをカバーする「整数の連番リスト」をメモリ上に作り出しています。
SEQUENCE(行, [列], [開始], [増分]) の形に当てはめて解説します。
- 行：省略（デフォルトの1）
- 列（個数）：
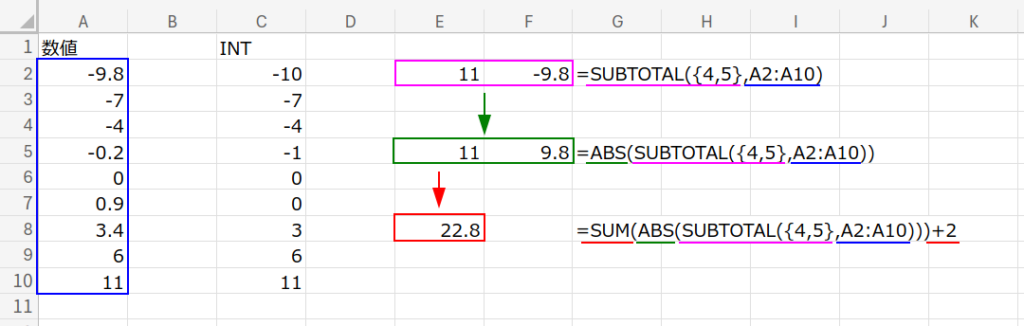
SUM(ABS(SUBTOTAL({4,5},A2:A10)))+2- 目的：連番を「何個」作ればいいかを計算しています。
SUBTOTAL({4,5}, ...)：配列定数{4,5}を使い、範囲内の「最大値(MAX)」と「最小値(MIN)」を同時に取得します。（例：最大11、最小-9.8）ABS(...)：それぞれの絶対値を取ります。（例：11、9.8）SUM(...)：それらを足し合わせます。（例：20.8）これで「データの振り幅（0をまたぐ範囲の広さ）」を確保しています。...+2：端数処理や範囲の余裕を持たせるために2個プラスしています。これで「約22個文の整数を作ろう」と決定します。
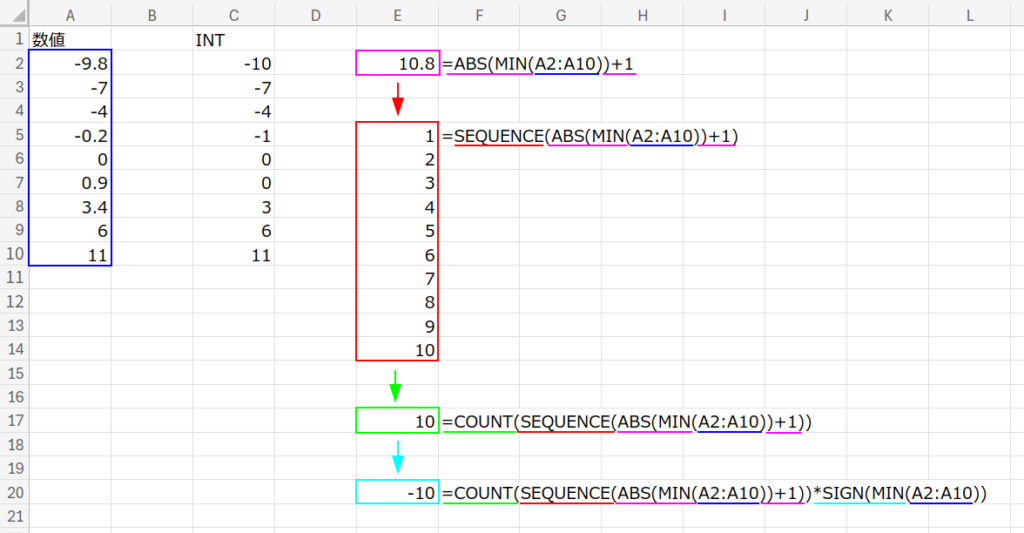
- 開始（スタート値）：
COUNT(SEQUENCE(ABS(MIN(A2:A10))+1))*SIGN(MIN(A2:A10))- 目的：連番を「いくつから」始めればいいか（最小の整数）を計算しています。INTやTRUNCを使わずに「-9.8」から「-10」を導き出すための執念のロジックです。
MIN(...)：最小値-9.8を取得。ABS(...)：絶対値9.8に変換。...+1：1を足して10.8にします。SEQUENCE(10.8)：ここがトリック！SEQUENCE関数は引数を整数に切り捨てる性質があります。つまりSEQUENCE(10)となり、1～10の配列ができます。COUNT(...)：その個数10を数えます。（これで擬似的に切り捨て整数10を作りました！）...*SIGN(...)：最後に元の符号（マイナス）を掛けて、スタート地点-10が完成します！
- 結果： これらを組み合わせると、
-10から始まり、1ずつ増える整数が約22個並んだ配列{-10, -9, -8, ..., 0, ..., 11, 12}が生成されます。これが「整数の定規」です。
③ LOOKUP関数の動作（ロジック）
最後に、LOOKUP関数がどう動くかです。
LOOKUP(検索値, 整数の連番配列)
LOOKUP関数（配列形式）は、データが昇順に並んでいる場合、「検索値以下で、最も大きい値（近似一致）」 を返します。
- 例：検索値
-9.8の場合 整数の連番{-10, -9, -8, ...}の中から探します。-9は-9.8より大きいのでダメ。-10は-9.8より小さい（以下である）。- したがって、
-9.8以下の最大整数である-10が選ばれます。
- 例：検索値
3.4の場合 整数の連番{..., 3, 4, ...}の中から探します。4は3.4より大きいのでダメ。3は3.4より小さい（以下である）。- したがって、
3.4以下の最大整数である3が選ばれます。
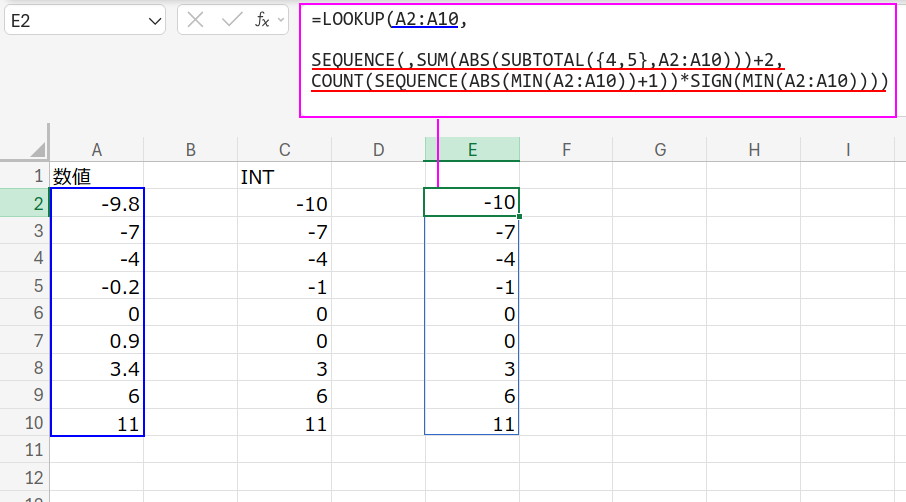
「検索値以下の最大整数を返す」というLOOKUPの挙動を利用することで、見事にINT関数の定義（数値を小さい方向の整数に丸める）を再現しているのです！
まとめ：回り道で見える「関数の本質」
たった一つの「整数にする」という操作でも、MODの余りの性質を利用したり、LOOKUPの近似一致を利用したりと、様々なルートがあることが分かりました。
実務では迷わず INT や FLOOR.MATH を使うべきですが、「なぜそうなるのか？」を考えると、Excel関数の奥深い世界が見えてきます。
特に「負の数の丸め」は、プログラミングやデータ分析でも意外な落とし穴になるポイントです。この感覚を掴んでおけば、きっとどこかで役に立つはずですよ！
