はじめに:懐かしの「連立方程式」、Excelなら一瞬です。
皆さん、中学校の数学の時間を思い出してください。
りんごを3つとみかんを2つ買うと、760円でした。
りんごを5つとみかんを3つ買うと、1240円でした。
りんごとみかん、それぞれ1ついくらでしょうか?
「うっ…頭が痛い…」と思った方もご安心ください!
自分の頭で計算する必要はありません。
この「連立方程式」こそ、Excelが最も得意とする分野の一つなのです。
本記事では、無料のWeb版Excelを使用して検証および画像の作成を行っています。Windowsはもちろん、MacやLinuxの方もブラウザさえあれば挑戦できます!
なぜ、いま連立方程式なのか?
「りんごの値段なんて知らなくていいよ」と思うかもしれません。
でも、この考え方はビジネスのあらゆる場面で使えます。
- 原価計算: 製品Aと製品Bの製造にかかった総コストから、部品単価を割り出す。
- 人員配置: チームごとの成果と人数から、1人あたりの生産性を分析する。
- 鶴亀算(つるかめざん): 足の数の合計から、ツルとカメが何匹いるか計算する(これは趣味ですね笑)。
複数の条件が絡み合う問題をスパッと解決する。それが連立方程式の力です。
今回は、この問題を5つの異なるアプローチで解いてみましょう!
ステップ1:冒険の準備 – 情報を整理する
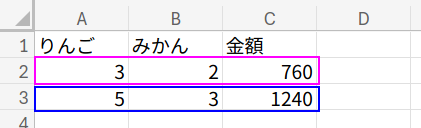
まずは、問題をExcelに入力しやすい形(行列)に整理します。
A1セルを起点に、以下の表を作成してください。
={"りんご","みかん","金額";3,2,760;5,3,1240}
【表の見かた(横方向に見ます)】
・2行目: りんご3個 + みかん2個 = 760円
・3行目: りんご5個 + みかん3個 = 1240円
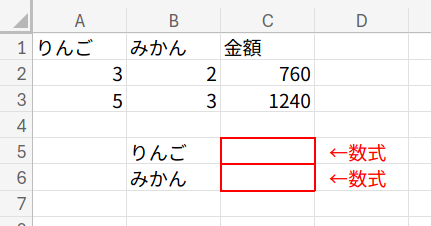
そして、答えを表示する場所を用意しましょう。
B5セルに「りんご」、B6セルに「みかん」と入力してください。
C5セルとC6セルに、これから紹介する数式を入れていきます。
5つの解法で、価格を暴き出せ!
関数の詳細な仕様については、Microsoft公式のヘルプも参考にしてください。
1. 中学校で習った方法(クラメルの公式)
考えかた
まずは、数学の教科書通りの解き方をそのままExcelの数式にします。
「![]() (りんご)を消して
(りんご)を消して ![]() (みかん)を求める公式」を当てはめる方法です。
(みかん)を求める公式」を当てはめる方法です。
数式
C5セル(りんご):=(C2*B3-C3*B2)/(A2*B3-A3*B2)
C6セル(みかん):=(C2-A2*((C2*B3-C3*B2)/(A2*B3-A3*B2)))/B2
この数式、実は「クラメルの公式」と呼ばれる、連立方程式の解の公式を手動で展開したものです。
解説
りんごの単価を ![]() 、みかんの単価を
、みかんの単価を ![]() とすると、以下のような式になります。
とすると、以下のような式になります。
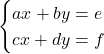
これを解く公式は、次のようになります。
![]()
Excelの数式を見てみてください。
(C2*B3-C3*B2) が分子の ![]() 、
、(A2*B3-A3*B2) が分母の ![]() に対応しているのが分かりますか?
に対応しているのが分かりますか?

「クロスして掛けて引く」という計算をしていますね!

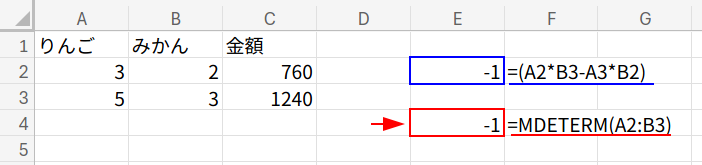
2. MDETERM関数 – 行列式の利用
考えかた
アプローチ1の「クロスして掛けて引く (![]() )」という計算、実は専用の関数があります。
)」という計算、実は専用の関数があります。
数式
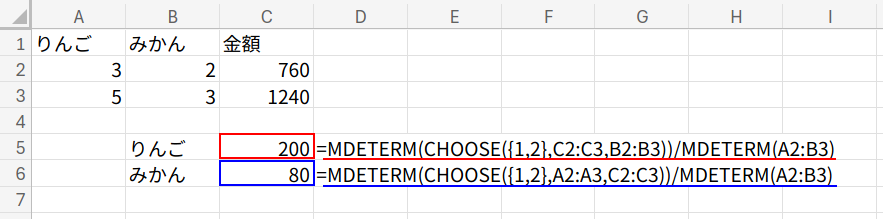
C5セル(りんご):=MDETERM(CHOOSE({1,2},C2:C3,B2:B3))/MDETERM(A2:B3)
C6セル(みかん):=MDETERM(CHOOSE({1,2},A2:A3,C2:C3))/MDETERM(A2:B3)
解説
・MDETERM(配列): 正方行列の「行列式(Determinant)」を返す関数です。
行列式とは、行列の特徴を表す数値のことです。
2×2の行列 ![]() の場合、行列式は
の場合、行列式は ![]() になります。
になります。
つまり、アプローチ1で一生懸命入力した計算式(C2*B3-C3*B2)は、MDETERM(A2:B3) と書くだけで求められるのです!
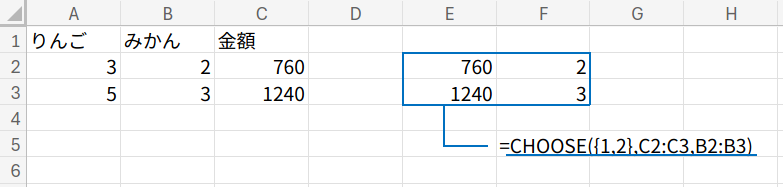
・CHOOSE({1,2}, …): ここがテクニック!本来の表の一部を、合計金額(C列)と入れ替えた仮想的な表をメモリ上に作っています。
これで行列式を計算し、割ることで答えを出しています(これもクラメルの公式そのものです)。
3. MMULT & MINVERSE – 行列計算が輝く瞬間
考えかた
ここからは、Excelの「行列計算」の真骨頂です。
最もスマートで数学的に美しい解法です。
数式
C5セル(スピルします):=MMULT(MINVERSE(A2:B3),C2:C3)
なぜこれで解けるのでしょう?
ロジックを解説します。
解説
今回の問題は、行列を使って以下のように書けます。
![]()
これをシンプルに ![]() と書きます。
と書きます。
(![]() は個数、
は個数、![]() は単価、
は単価、![]() は金額)
は金額)
私たちが知りたいのは ![]() (単価)です。
(単価)です。
普通の方程式 ![]() なら、両辺を3で割れば(または
なら、両辺を3で割れば(または ![]() を掛ければ)答えが出ますよね?
を掛ければ)答えが出ますよね?
行列の世界には「割り算」はありませんが、代わりに「逆行列(![]() )」というものを掛けます。
)」というものを掛けます。
これは数字で言う「逆数(![]() )」のような存在です。
)」のような存在です。
![]()
つまり、「個数の表(![]() )の逆行列」に「金額(
)の逆行列」に「金額(![]() )」を掛ければ、一発で単価(
)」を掛ければ、一発で単価(![]() )が出るのです!
)が出るのです!
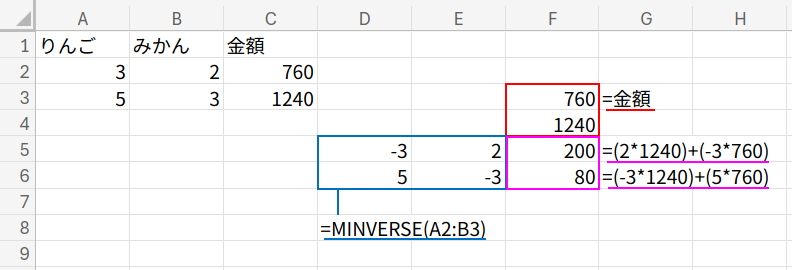
1. MINVERSE(A2:B3): 個数の範囲(![]() )の「逆行列」を計算します。
)の「逆行列」を計算します。
2. MMULT(逆行列, C2:C3): その逆行列と、金額の範囲(![]() )を「行列積(MMULT)」で掛け合わせます。
)を「行列積(MMULT)」で掛け合わせます。
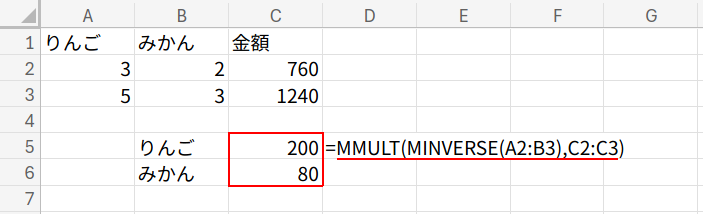
MMULT関数については以下の記事でも紹介しています。
4. LINEST関数 – 統計関数の応用
考えかた
LINESTは、本来は「回帰分析(データの傾向線を引くなど)」に使われる統計関数です。
「このデータに最もよく当てはまる直線の式を見つけて!」という時に使います。
数式
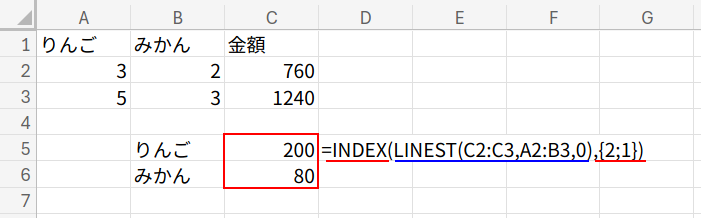
C5セル(スピルします):=INDEX(LINEST(C2:C3,A2:B3,0),{2;1})
解説
なぜLINESTで解けるの?
今回の問題は、「合計金額 = りんごの単価 × りんご個数 + みかんの単価 × みかん個数 + 0」という式で表せます。
これは統計学で言う「重回帰分析」の式 ![]() と全く同じ形なんです!
と全く同じ形なんです!
この記事の目的は統計学の講義ではないので、詳しい理論の解説は省略します。
「そういう便利な関数があるんだ」くらいの感覚でOKです!
LINEST関数に「金額(y)」と「個数(x)」を渡せば、それにぴったり合う「単価(係数m)」を計算してくれます。
・LINEST(既知のy, 既知のx, 定数, 補正): 第3引数を0(FALSE)にすることで、切片bを0に固定して計算させています。
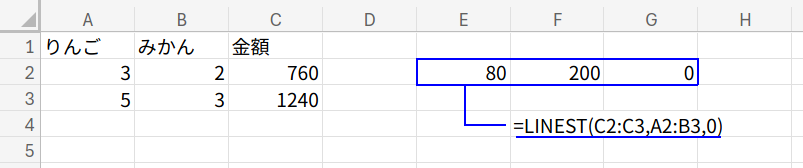
・INDEX(…, {2;1}): LINEST関数は、係数を「後ろから順(みかん→りんご)」に返すという癖があります。
そのため、INDEX関数で順番を {2;1} と入れ替えて、りんご→みかんの順に直しています。
「傾向を知るための関数」で「正解」を出す。なんだか裏技っぽくてワクワクしませんか?
5. シミュレーション(総当たり)攻撃!
考えかた
最後は、数学なんて知ったことか!という力技です。
「りんごが0個なら…1個なら…2個なら…」とすべての可能性を計算し、条件に合うものを見つけ出します。
PCの計算力を活かした「全探索」アプローチです。
数式
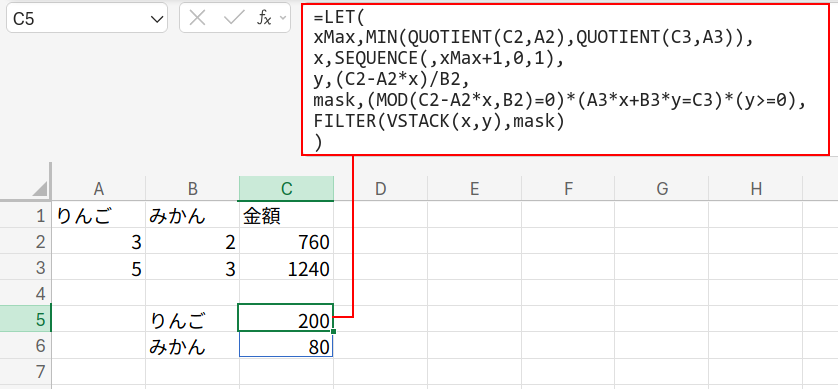
C5セル(スピルします):=LET(xMax,MIN(QUOTIENT(C2,A2),QUOTIENT(C3,A3)),x,SEQUENCE(,xMax+1,0,1),y,(C2-A2*x)/B2,mask,(MOD(C2-A2*x,B2)=0)*(A3*x+B3*y=C3)*(y>=0),FILTER(VSTACK(x,y),mask))
ものすごく長いですが、やっていることは単純です。
解説
1. xMax: 「りんごを最大何個買えるか?」を計算します。(予算÷単価のイメージ)
=MIN(QUOTIENT(C2,A2),QUOTIENT(C3,A3))

2. x: りんごの価格としてあり得る「0円から最大価格まで」のリストを作ります。
=SEQUENCE(,xMax+1,0,1)

3. y: 「もしりんごがx円なら、みかんは何円になるか?」を逆算します。
=(C2-A2*x)/B2
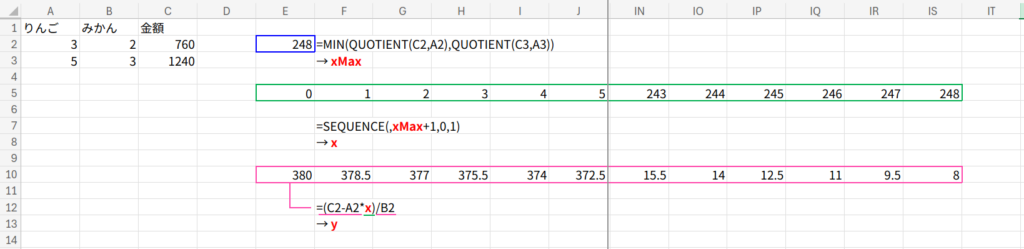
4. mask (条件判定): ここでフィルターを作ります。
=(MOD(C2-A2*x,B2)=0)*(A3*x+B3*y=C3)*(y>=0)
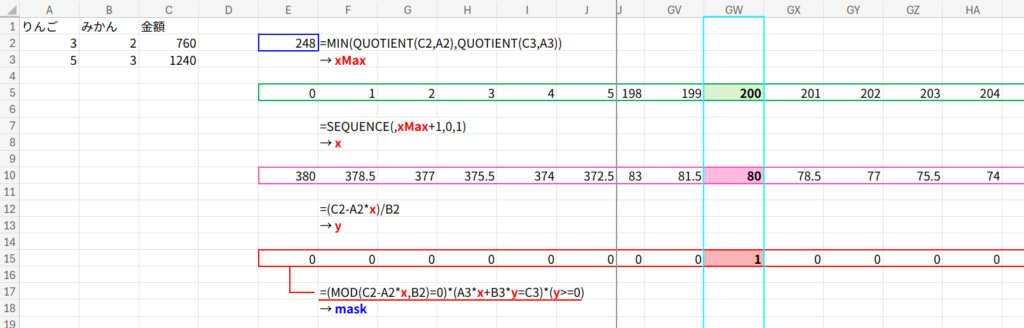
(MOD...=0): みかんの価格が「整数」になっているか?(割り切れるか)(A3*x+B3*y=C3): 2つ目の条件式(5個と3個で1240円)も満たしているか?(y>=0): みかんの価格がマイナスになっていないか?
5. FILTER: 全ての条件を満たす「りんご(x)」と「みかん(y)」のペアだけを抜き出します。
=FILTER(VSTACK(x,y),mask)
【注意点】
この方法は「単価は0以上の整数である」という前提で総当たりしています。
もし答えがマイナスになる場合(数学的にはあり得ます)や、整数にならない場合、この数式は答えを見つけられず #CALC! エラーになります。
まとめ:Excelは「最強の電卓」だ
答えは「りんご:200円、みかん:80円」でしたね!
普通なら紙とペンで計算する問題も、Excelにかかれば MMULT 一発で解けたり、あるいは LET と SEQUENCE で力技で解けたりと、様々なアプローチが可能です。
この考え方は、ビジネスでの「最適な組み合わせ探し」や「コスト分析」にも応用できます。
「あ、これ連立方程式だな」と思ったら、ぜひExcelを開いて、行列計算やシミュレーションを試してみてくださいね!