はじめに：そのグラフ、円グラフの親戚ではありません
Excelのグラフの中に、「レーダーチャート」というものがあります。
ゲームのキャラクターのステータス画面（攻撃力、守備力、素早さ…みたいな五角形や六角形のやつ）でよく見る、アレです。
普段はデータのバランスを見るために使われますが、今回はこのレーダーチャートを「お絵かきツール」として使ってしまいます！
以下の記事では散布図を使用した図形を紹介しています！興味ある方はぜひ！
Excelグラフで図形を描こう！【コピペOK】
Excelグラフアート！ハートとダイヤの描き方
「極座標」ってなに？
私たちが普段、Excelの表や散布図で使っているのは、「横にX行って、縦にY上がる」という場所の決め方です。
これを「デカルト座標（直交座標）」と呼びます。
対して、今回使うのは「極座標（きょくざひょう）」です。
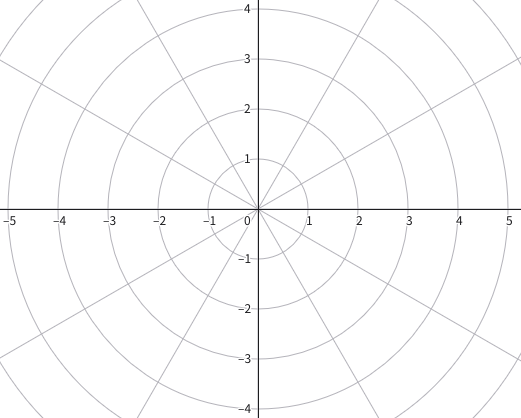
これは、「中心から角度 
(シータ) の方向に、距離 
(アール) だけ進んだ場所」という決め方をします。
レーダーチャートは、まさにこの「中心からの距離」をプロットするグラフなので、これを利用して不思議な図形を描こう！というわけです。
本記事では、無料のWeb版Excelを使用して検証および画像の作成を行っています。Windowsはもちろん、MacやLinuxの方もブラウザさえあれば挑戦できます！
キャンバスの準備 – 「ラジアン」を知ろう
まずは準備です。まっさらなシートを用意してください。
Excelの三角関数（SINやCOS）は、角度を「度（°）」ではなく「ラジアン」という単位で扱います。
難しいことは考えなくてOK！「180° ＝ 
(パイ) ラジアン」とだけ覚えておけば大丈夫です。
A1セルに「RADIANS」と入力し、A2セルに以下の数式を入力してください。
=SEQUENCE(361,,0,PI()/180)
【解説】
・361: 0度から360度まで、ぐるっと一周分のデータを作ります。
・0: スタートは0度。
・PI()/180: これが「1度」分のラジアンです。1度ずつ増やしていきます。
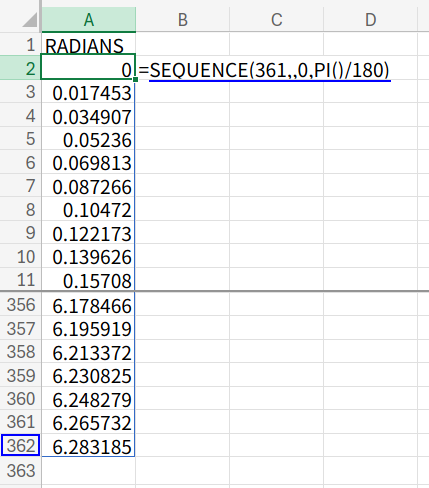
これで、A列に0から約6.28（
）までの数値がズラッと並びました。これが「角度（）」になります。
7つの数式でアートを描こう！
さあ、ここからはB列（距離 ）に数式を入れて、グラフを描いていきます。
B2セルに数式を入力するだけで、図形が変わりますよ！
数式1：基本の「花びら」 (SIN関数)
数式
=SIN(8*A2#)
グラフの作成手順（最初だけ詳しく！）
1. B2セルに数式を入力すると、スピルして数値が表示されます。
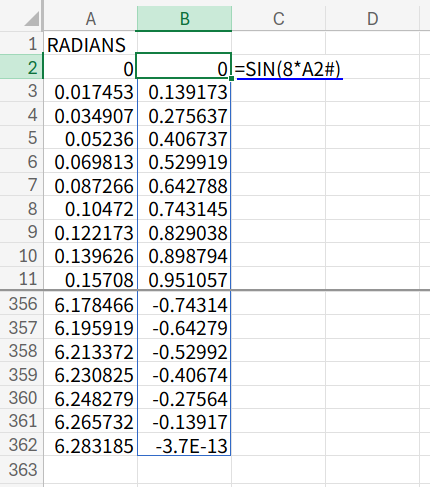
2. B列のデータ範囲を選択します。
3. 「挿入」タブ → 「その他のグラフ」 → 「レーダー」を選択します。
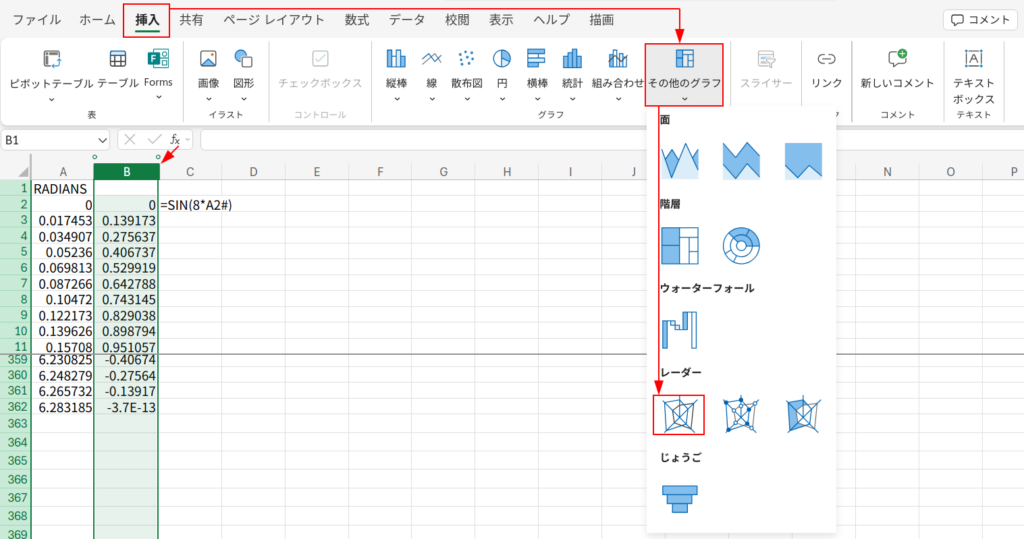
【重要：グラフをスッキリさせる】
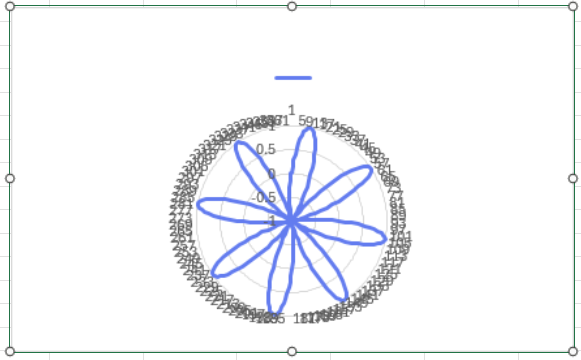
デフォルトだとごちゃごちゃしているので、整形しましょう。
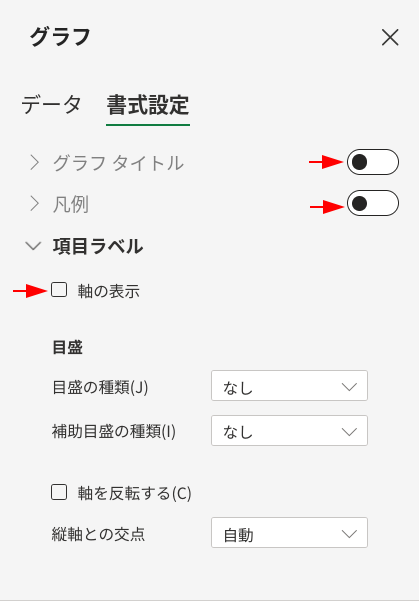
グラフを選択し、「グラフ」タブ→「書式設定」を開きます。
- 「グラフ タイトル」：なし
- 「凡例」：なし
- 「軸の表示（項目ラベル）」：なし
仕上げに、Shiftキーを押しながらグラフの角をドラッグして拡大縮小すると、縦横比が固定されてきれいな正方形になります。
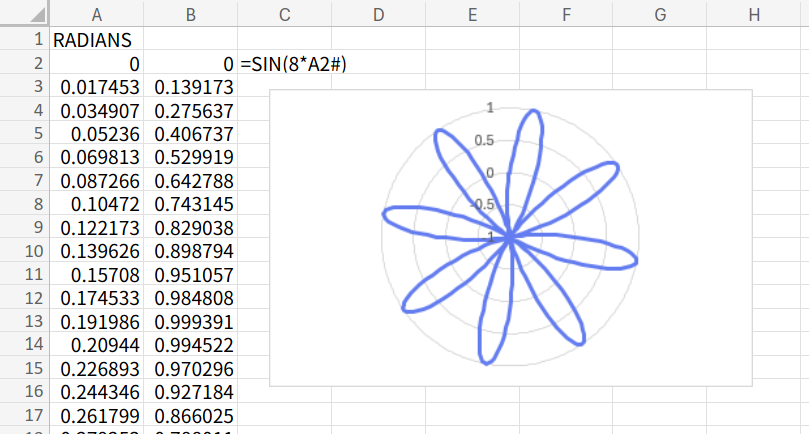
解説
SIN関数は波の形を作ります。
それを円状に配置すると、波の山と谷が「花びら」のようなループになります。
「8」という数字を変えると、花びらの枚数が変わりますよ！
数式2：複雑な波紋 (SINの重ね合わせ)
数式
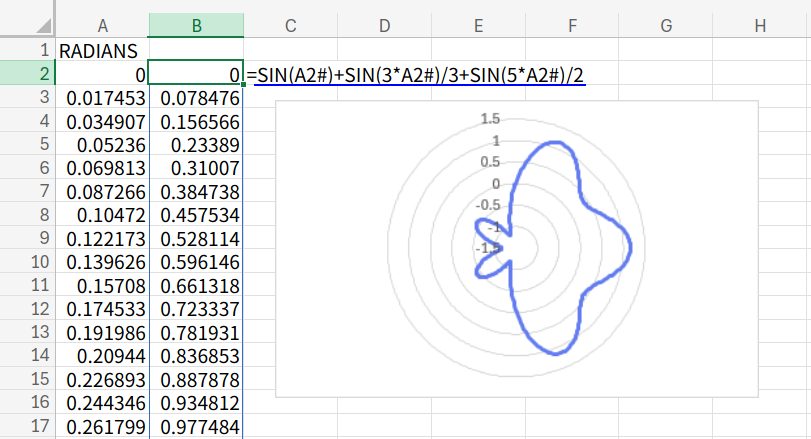
=SIN(A2#)+SIN(3*A2#)/3+SIN(5*A2#)/2
解説
大きさや細かさ（周波数）の違う波を3つ足し合わせました。
単調だった花びらが、より複雑で有機的な、本物の植物のような形になりましたね。
数式3：蝶々？それとも… (SIN + COS)
数式
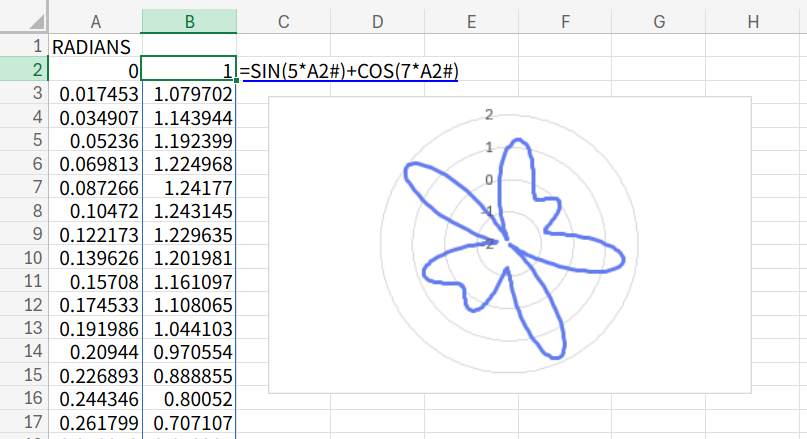
=SIN(5*A2#)+COS(7*A2#)
解説
SIN（正弦）とCOS（余弦）を、異なるリズム（5と7）で組み合わせてみました。
規則的なのにどこか不安定な、蝶々が羽を広げたような、あるいは不思議な葉っぱのような形が現れます。
数式4：ギザギザ・モンスター (高周波)
数式
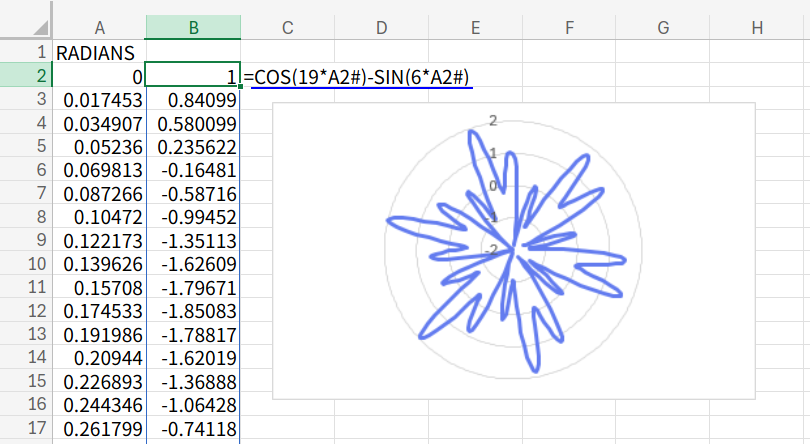
=COS(19*A2#)-SIN(6*A2#)
解説
「19」という大きな数字を掛けることで、波を細かくしています。
全体がギザギザになり、ウニや攻撃的な星のような図形になります。
数式5：デジタルな結晶 (CEILING関数)
数式
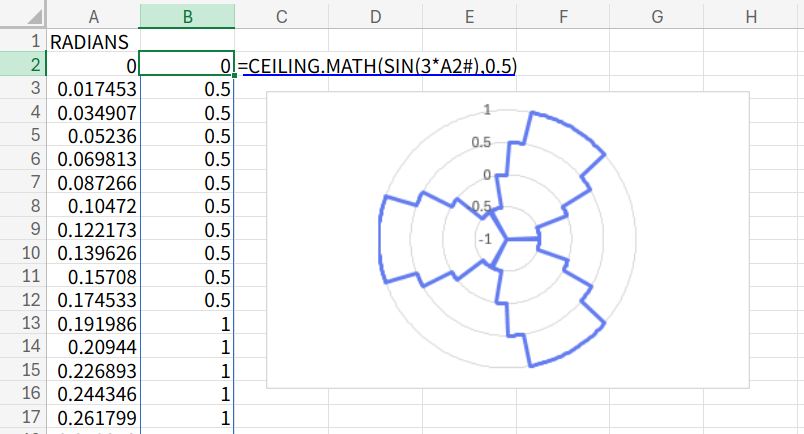
=CEILING.MATH(SIN(3*A2#),0.5)
解説
数値を「0.5単位」で切り上げています。
その結果、距離 は「-1, -0.5, 0, 0.5, 1」のいずれかしか取りません。
滑らかな曲線がなくなり、カクカクとしたデジタルな結晶のような幾何学模様になります。
数式6：鋭い刃 (MOD関数)
数式
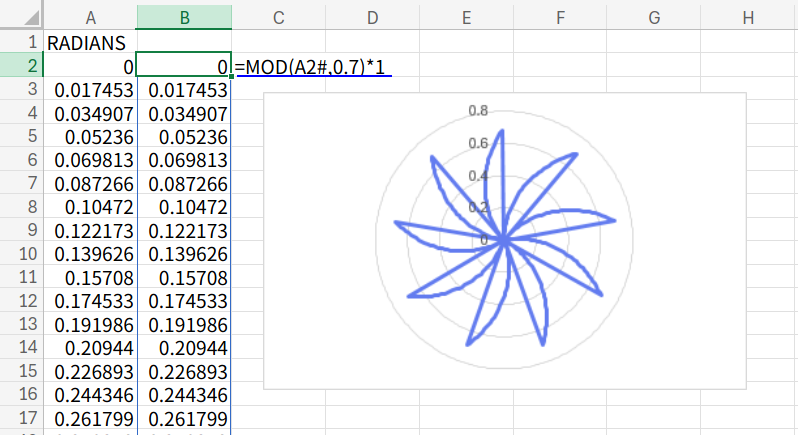
=MOD(A2#,0.7)*1
解説
MOD関数で割り算の余りを出すと、「0から増えていって、0.7になったらストンと0に戻る」というノコギリ波ができます。
これを極座標で描くと、中心から外へ向かって急激に戻る、鋭い刃（ファン）のような形になります。
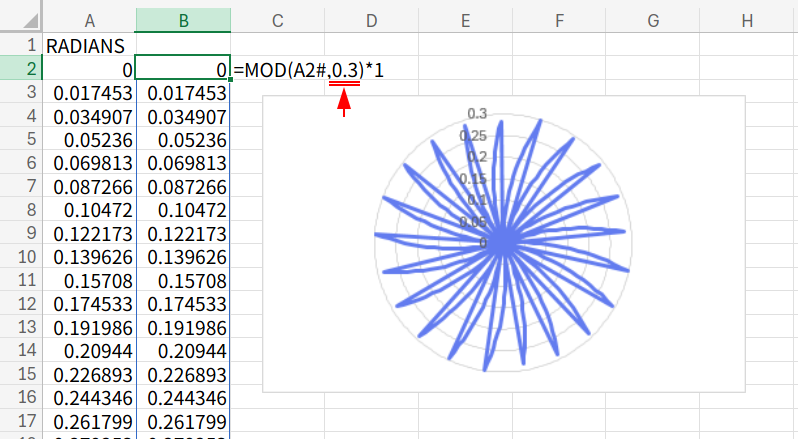
「0.7」の値を小さくすると、刃の枚数が増えますよ！
数式7：12等分のケーキ (IF関数)
数式
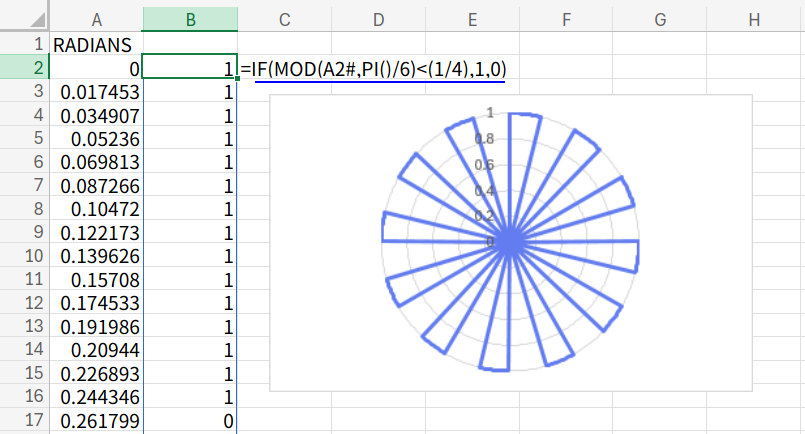
=IF(MOD(A2#,PI()/6)<(1/4),1,0)
解説
これは「距離が 1 か 0 か」しかない世界です。
角度によって、ある期間は「1（外周）」、ある期間は「0（中心）」と切り替えることで、細いケーキのピースが並んだような、あるいは機械のギアのような図形が描けます。
まとめ：数式は、最高のおもちゃだ。
Excelのグラフは、売上や推移を表示するためだけの道具ではありません。
数式の「係数（掛け算する数字）」を「3」から「4」に変えるだけで、花びらの枚数が増えたり、全く違う形に変貌したりします。
ぜひ、今回紹介した数式の数字を適当にいじってみてください。
「うわっ、なんだこれ！？」という奇妙な図形が生まれたとき、あなたはもうExcelの虜になっているはずです。
これからも、Excelで「（実務では）役に立たないけど面白いこと」を追求していきましょう！
