はじめに：Excelで「分数の足し算」できますか？
いきなりですが、問題です。
「そんなの簡単だ！えーっと、通分して…答えは だ！」
正解です!
手計算でなくても、電卓ソフトを使えば簡単に計算ができますよね！（※以下、Qalculate!の計算結果）
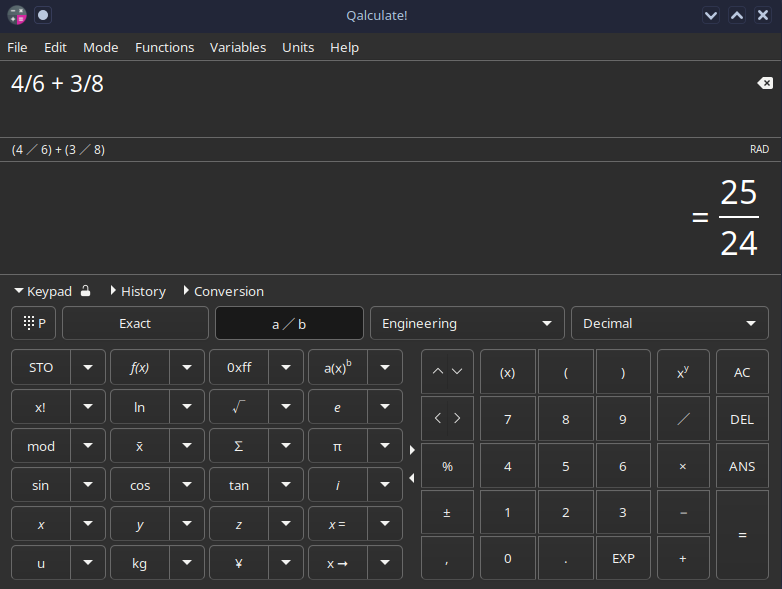
では、これをExcelで計算してください。
普通にセルに =4/6 + 3/8 と入力するとどうなるでしょうか？
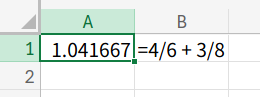
答えは 1.041666667... という小数が表示されてしまいます。
「セルの書式設定で『分数』にすればいいじゃん！」と思った方、鋭いですが惜しいんです。
Excelの分数表示はあくまで「近似値」を表示するもので、計算過程で正確な「通分」や「約分」をしてくれるわけではありません。
そこで今回は、「分子」と「分母」を別々のセルに入力し、数式で数学的に処理をすることで、小学校で習った「分数の足し算」をExcel上で完全再現してみたいと思います！
ミッション：セルを使って筆算を再現せよ
今回のゴールは、以下のような計算フォームを作ることです。
配置ルール
- A列：1つ目の分数（A1に分子、A2に分母）
- B列：「＋」記号（B1:B2を結合）
- C列：2つ目の分数（C1に分子、C2に分母）
- D列：「＝」記号（D1:D2を結合）
- E列：答えの分数（E1に分子、E2に分母）
今回は例として、以下の数値を入力してみましょう。
です。
- A1：4
- A2：6
- C1：3
- C2：8
カギを握るのは「最大公約数」
さて、これを計算するために絶対に必要なものがあります。
それは「約分（やくぶん）」の処理です。
例： →
分数の足し算をした後、数字が大きくなりすぎないように、分子と分母を「共通して割れる一番大きな数」で割る必要がありますよね。
この「共通して割れる一番大きな数」のことを、数学用語で、
「最大公約数（Greatest Common Divisor）」と呼びます。
Excelには、これを一発で求めてくれる便利な関数が存在します。
=GCD(数値1, 数値2)
たとえば空いているセルに =GCD(6, 8) と入力してみてください。
6と8の最大公約数である「2」が返ってくるはずです。
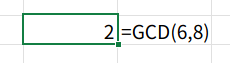
【暇つぶしコラム】GCD関数を使わずに最大公約数を求めよ
ここで少し脱線して、頭の体操です。
もしExcelにGCD関数がなかったら、どうやって最大公約数を求めますか？
関数の動きを分解して理解するために、あえて自力で数式を組んでみましょう。
最近のExcel（動的配列対応）なら、こんな数式で求められます。
=MAX((MOD(A1,SEQUENCE(MIN(A1,A2)) )=0)*(MOD(A2,SEQUENCE(MIN(A1,A2)) )=0)*(SEQUENCE(MIN(A1,A2)) ))
「うわっ、なんだこれ！」と思うかもしれませんが、分解すると非常にシンプルです。
1. 割る数の候補を作る：SEQUENCE
MIN(A1,A2) で2つの数字のうち小さい方を選び、SEQUENCE で1からその数までの連番を作ります。
（例：4と6なら、1, 2, 3, 4）
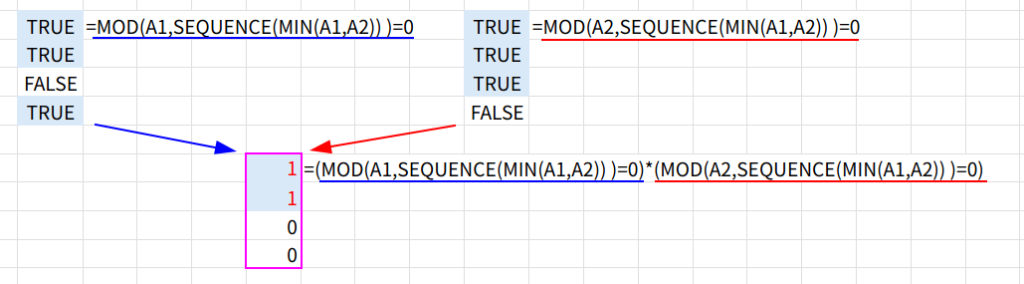
2. 割り切れるかチェック：MOD
MOD(A1, 連番)=0 で、A1がその数で割り切れるかを判定します。MOD(A2, 連番)=0 で、A2も割り切れるかを判定します。
3. 両方割り切れる数だけ残す
2つの判定結果を掛け算（AND条件）すると、「両方の約数である数」の場所だけが「1」になります。
そこに元の連番を掛け合わせると、公約数のリストが出来上がります。
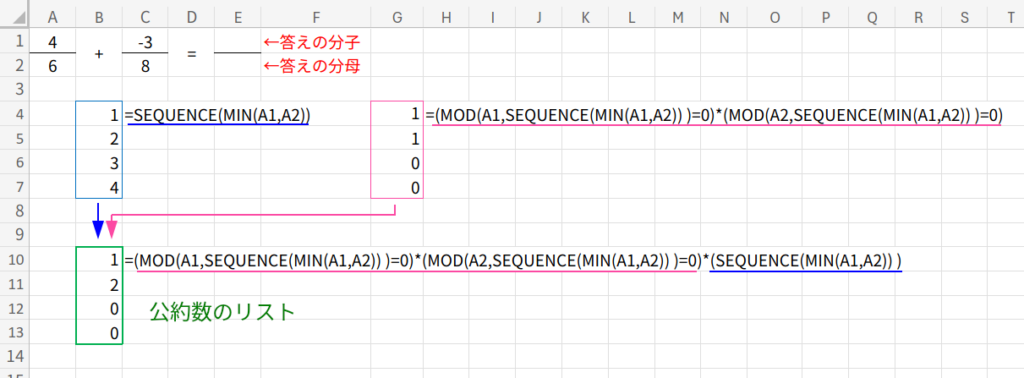
4. 最大値を選ぶ：MAX
最後に MAX 関数で、そのリストの中から一番大きい数を取り出せば…、最大公約数の完成です！
普段何気なく使っている関数も、こうして中身を考えると面白いですよね。
いざ実装！数式を入力しよう
では、本題に戻りましょう。
E列の「答え」のセルに数式を入力します。
分数の足し算の公式は、以下の通りです。
（通分して、たすき掛けで足します）
これをそのまま数式にし、最後にGCD関数で約分すれば完璧です！
E1セル（答えの分子）
=(A2*C1+A1*C2)/GCD(A2*C1+A1*C2,A2*C2)
E2セル（答えの分母）
=A2*C2/GCD(A2*C1+A1*C2,A2*C2)
これで を計算すると、E1に「25」、E2に「24」が表示されるはずです。
正解ですね！
しかし、この数式には「致命的な弱点」がある
完璧に見えるこの計算機ですが、実はある条件下でエラーになります。
A1セル（分子）を「-6」に変えてみてください。
計算式は になるはずです。
しかし、結果は…#NUM! エラー！！
なぜでしょうか？
実は、ExcelのGCD関数は「負の数」に対応していないのです。
引数にマイナスの値が入ると、計算を放棄してエラーを返してしまいます。
解決策：絶対値（ABS）でGCDを騙せ！
でも、諦める必要はありません。
最大公約数というのは、数の「大きさ」に対する性質なので、プラスでもマイナスでも変わりません。（-6と4の最大公約数も、6と4と同じく2です）
つまり、GCD関数に渡すときだけ、無理やりプラスの数（絶対値）にしてしまえばいいのです。
ABS関数を使って、数式を以下のように修正しましょう。
E1セル（答えの分子・修正版）
=(A1*C2+C1*A2)/GCD(ABS(A1*C2+C1*A2),ABS(A2*C2))
E2セル（答えの分母・修正版）
=A2*C2/GCD(ABS(A1*C2+C1*A2),ABS(A2*C2))
こうすることで、計算自体はマイナスのまま行い、約分の判定だけをプラスの数で行うことができます。
検証：負の数同士の足し算
実際に、別の数値で試してみましょう。
- A1：-7
- A2：4
- C1：-3
- C2：5
という計算ですね。
結果は… E1: -47、E2: 20。
見事、 が表示されました！大成功です！
まとめ：工夫次第でExcelはもっと賢くなる
「分数の足し算」という、一見Excelが苦手そうなテーマでしたが、セルの使い方と数学的なロジックを組み合わせることで、完璧な計算機を作ることができました。
標準機能でできないことも、こうして工夫して乗り越える過程こそが、Excelパズルの面白いところです。
みなさんもぜひ、身近な計算をExcelで「再発明」して遊んでみてくださいね！
