はじめに:Excelは「表計算ソフト」であり「行列計算機」である
皆さん、中学や高校の数学の授業を思い出してください。
こんな問題に頭を抱えたことはありませんか?
「鶴と亀が合わせて10匹います。足の数は合わせて28本です。鶴と亀は何匹?」
いわゆる「つるかめ算」、数学的に言えば「連立方程式」ですね。
変数が2つ(![]() )ならまだしも、3つ(
)ならまだしも、3つ(![]() )になると、
)になると、
手計算では計算ミスが多発して絶望的な気分になります。
しかし、Excelには「行列(Matrix)」を扱うための強力な関数が備わっています。
これを使えば、変数が2つだろうが、10個だろうが、たとえ100個あろうとも、
一瞬で答えを導き出すことができます。
Excelはただの表計算ソフトではなく、超高性能な「連立方程式・自動解答マシーン」なのです。
本記事では、無料のWeb版Excelを使用して検証および画像の作成を行っています。Windowsはもちろん、MacやLinuxの方もブラウザさえあれば挑戦できます!
※連立方程式については、以下の記事で様々な解法を紹介しています!
行列計算ができると何が嬉しいの?
「数学なんて実務で使わないよ」と思うかもしれませんが、この知識があると以下のような場面で役立ちます。
- 損益分岐点の分析: 複数の製品のコストと利益のバランスを計算する。
- 配合の最適化: 複数の原料を混ぜて、目標の成分値にするための比率を出す。
- データ補間: 点と点の間を埋める直線の式を求める。
今回は、MMULT(行列の積)と MINVERSE(逆行列)という2つの関数を使って、日常にありそうな6つの問題を鮮やかに解いてみせます。
関数の詳細な仕様については、Microsoft公式のヘルプも参考にしてください。
数学の時間:なぜExcelで行列を解くのか?
まずは少しだけ、数学の話にお付き合いください。
連立方程式を行列で表すと、以下のようになります。
![]()
- A:係数行列(左辺の数字の塊)
- X:変数行列(求めたい
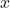 や
や 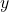 )
) - B:定数行列(右辺の答え)
ここから X(答え) を求めたい場合、どうすればいいでしょうか?
普通の数式なら「Aで割る(![]() )」ところですが、残念ながら行列の世界に「割り算」はありません。
)」ところですが、残念ながら行列の世界に「割り算」はありません。
その代わり、「逆行列(![]() )」というものを掛けます。
)」というものを掛けます。
イメージとしては、「逆数を掛ける(![]() )」のと似ています。
)」のと似ています。
![]()
つまり、「係数の逆行列」と「答え」を掛け算すれば、一発で変数が求まるのです。
これをExcel関数に翻訳すると、こうなります。
=MMULT( MINVERSE(係数行列), 答え行列 )
この魔法の数式を使って、次々と問題を解いていきましょう!
問題1:チケットの売上枚数(基本)
【問題】
前売り券(2,000円)と当日券(3,000円)を合わせて50枚販売し、売上は115,000円でした。
それぞれ何枚売れたでしょうか?
考え方と数式
はじめに、前売り券を ![]() 、当日券を
、当日券を ![]() として式を立てます。
として式を立てます。
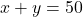 (枚数)
(枚数)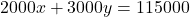 (金額)
(金額)
これをExcelの行列数式に当てはめます。
=MMULT(MINVERSE({1,1;2000,3000}),{50;115000})
【解説】
1. {1,1;2000,3000}:これが係数行列Aです。セミコロン(;)で行を変えています。

2. MINVERSE(...):この関数の逆行列(![]() )を計算します。これぞExcelの力!
)を計算します。これぞExcelの力!

3. {50;115000}:これが答え行列Bです。
4. MMULT(...):逆行列と答え行列を掛け合わせ、最終的な解(![]() )を算出します。
)を算出します。

答え:前売り券 35枚、当日券 15枚
【実務でのポイント】
記事では分かりやすく数値を直接入力していますが、実務ではセル範囲(A1:B2など)を選択して計算できます。
係数や答えをセルに入力しておけば、あとは数字を書き換えるだけで、あらゆる問題を解ける「万能計算機」になります!
問題2:直線の式を求める(幾何学)
【問題】
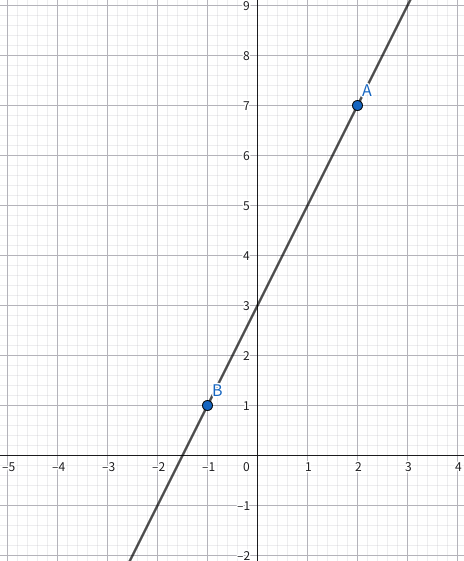
座標 ![]() と
と ![]() の2点を通る直線の式
の2点を通る直線の式 ![]() の傾き
の傾き ![]() と切片
と切片 ![]() を求めよ。
を求めよ。
懐かしいですね!中学数学でやった一次関数です。
考え方と数式
連立方程式を立てます。
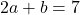 (
(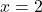 のとき
のとき 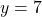 )
)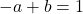 (
(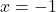 のとき
のとき 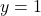 )
)
=MMULT(MINVERSE({2,1;-1,1}),{7;1})

答え:傾き(a) = 2、切片(b) = 3
【エラーになるケース】
もし2点のx座標が同じ(例:(2, 7)と(2, 5)など)場合、直線は垂直になり「傾き」が無限大になります。
この時、行列の世界では「逆行列が存在しない(割り算で言うところの0除算)」状態となり、#NUM! エラーになります。
【別解】統計関数 LINEST を使う
実は、この手の問題は統計用の LINEST 関数でも解けます。
=TRANSPOSE(LINEST({7,1},{2,-1}))
解説:LINESTは「最小二乗法」を使って、点に最もフィットする直線を求める関数です。
点が2つだけなら、完璧にその2点を通る直線の解と一致します。
ただし、LINESTは結果を「横方向」に返します。
行列計算の結果(縦方向)と合わせるために TRANSPOSE で縦横を変換しています。

問題3:原価と定価(割合の計算)
【問題】
定価は原価の1.5倍です。
定価の7割で売ると、原価より840円多く残ります。
原価と定価はいくら?
考え方と数式
続いて、定価を ![]() 、原価を
、原価を ![]() とします。
とします。
式を整理して、「![]() 」の形にするのがコツです。
」の形にするのがコツです。
=MMULT(MINVERSE({1,-1.5;0.7,-1}),{0;840})

答え:定価 25,200円、原価 16,800円
問題4:道のりと時間(単位変換の応用)
【問題】
目的地まで、時速50kmの高速道路で行くのと、時速35kmの一般道で行くのでは、到着時間に18分の差が出ます。
高速道路を使った場合の所要時間(分)と目的地までの距離(km)は?
考え方と数式
ここが一番の難所です!「分」と「時速」が混ざっているので、単位を合わせる必要があります。
距離を ![]() (km)、高速の時間を
(km)、高速の時間を ![]() (時間) とします。
(時間) とします。
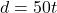
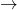
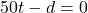
- 一般道の時間は、高速より18分(18/60時間)多いので、
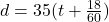
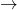
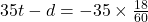
この連立方程式を解き、最後に時間を「分」に戻すために60倍します。
=MMULT(MINVERSE({50,-1;35,-1}),{0;-1}*(35*18/60))*{60;1}
【解説】
・{0;-1}*(35*18/60):右辺の行列を作っています。2つ目の式がマイナスになるため、ベクトル {0; -1} に値を掛けて表現しています。
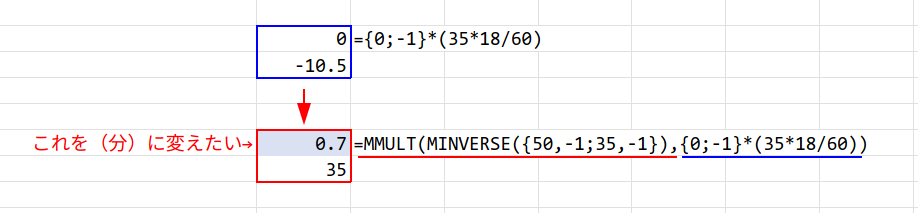
・*{60;1}:出てきた答えは「時間(h)」と「距離(km)」です。求めたいのは「分」なので、上の段(時間)だけ60倍しています。

答え:所要時間 42分、距離 35km
問題5:和差算(シンプルイズベスト)
【問題】
男女合わせて38名のチーム。男性は女性より6名多いです。
それぞれの人数は?
考え方と数式
行列で解くならこうです。
=MMULT(MINVERSE({1,1;1,-1}),{38;6})

【別解】行列を使わない方法
実はこの程度の問題なら、算数のテクニック(和差算)を使ったほうが早いです。
=(38+6*{1;-1})/2
解説:
「(合計 + 差) ÷ 2」で大きい方の数(男性)が、「(合計 – 差) ÷ 2」で小さい方の数(女性)が出ます。
6*{1;-1} で {6; -6} を作り、プラスの場合とマイナスの場合を一気に計算しています。

答え:男性 22名、女性 16名
問題6:3変数の連立方程式(ラスボス)
【問題】
ある文房具店のセット価格です。ペン・ノート・消しゴムの単価を求めてください。
セットA(ペンx3、ノートx2、消しゴムx1)= 850円
セットB(ペンx1、ノートx3、消しゴムx2)= 900円
セットC(ペンx2、ノートx1、消しゴムx3)= 710円
最後に、変数が3つ(![]() )になったラスボスの登場です。
)になったラスボスの登場です。
これを手計算で解こうとすると、「①と②から ![]() を消して、②と③からも
を消して、②と③からも ![]() を消して…」と、計算用紙が真っ黒になります。絶対にやりたくないですね!
を消して…」と、計算用紙が真っ黒になります。絶対にやりたくないですね!
しかし、Excelの行列計算なら、変数が2つでも3つでもやることは同じです。
考え方と数式
=MMULT(MINVERSE({3,2,1;1,3,2;2,1,3}), {850;900;710})
【解説】
係数行列が 3×3 になり、答え行列が 3行になっただけです。
{3,2,1; 1,3,2; 2,1,3} と入力するだけで、Excelが裏側で複雑な「掃き出し法」等の計算を一瞬で終わらせてくれます。
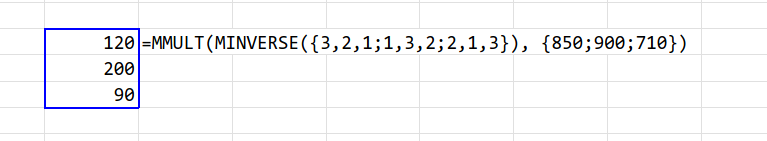
答え:ペン 120円、ノート 200円、消しゴム 90円
まとめ:数学の力でExcelを使いこなせ!
「行列」と聞くと難しそうに感じますが、Excelにおいては、
「複数の条件式を一発で解くための魔法のツール」です。
すなわち、MMULT と MINVERSE のコンビネーションを覚えておけば、ビジネスで複雑なクロス計算やシミュレーションが必要になった時、きっと強力な武器になるはずです。
ぜひ、身の回りの問題を「行列」に置き換えて、Excelに解かせてみてください!