はじめに:MATCH関数の限界に挑む?
Excelで「ある数字」がどこにあるかを探すとき、真っ先に思いつくのは MATCH関数 ですよね。
「1はどこ?」→「〇番目にあります!」と即答してくれます。
しかし、今回のミッションは少し違います。
「『1』の直後に『9』が来るパターンはどこ?」 を探したいのです。
通常のMATCH関数は、あくまで「1つのセル」しか見てくれません。
単に「1」を探すだけでは、後ろが「3」かもしれないし「8」かもしれません。「縦に並んだ2つのセル」をセットで検索する…。さあ、どうすればいいでしょうか?
実務ではこんな場面で役立ちます
「こんなパズル、いつ使うの?」と思うかもしれませんが、この考え方は実務データ分析の基礎になります。
- ログ分析: 「エラー発生」の直後に「システム停止」が起きた瞬間(原因)を特定する。
- 行動分析: 「商品ページ閲覧」の次に「購入ボタン」を押したユーザーの行動パターンを探す。
- センサーデータ: 温度が「急上昇」した直後に「急降下」した異常波形を見つける。
今回は、Excel初心者の方にも分かりやすいように、7つのアプローチでこの問題を解いていきます!
今回のターゲットデータ
本記事では、無料のWeb版Excelを使用して検証および画像の作成を行っています。Windowsはもちろん、MacやLinuxの方もブラウザさえあれば挑戦できます!
A1セルからA15セルに、以下の数字が入力されています。
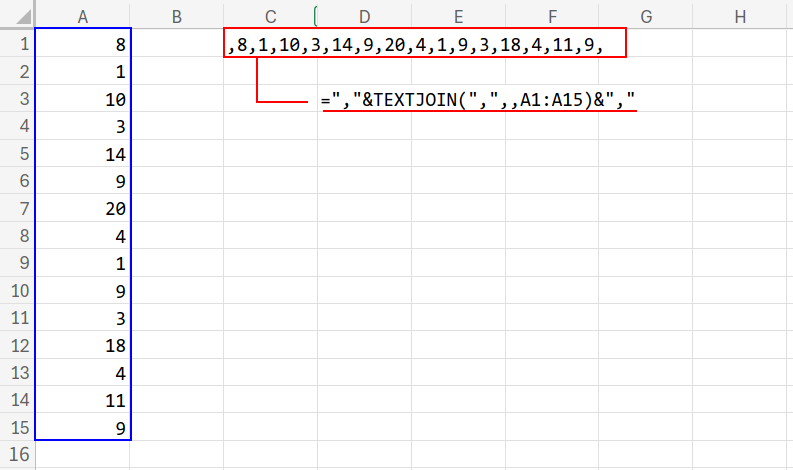
={8;1;10;3;14;9;20;4;1;9;3;18;4;11;9}
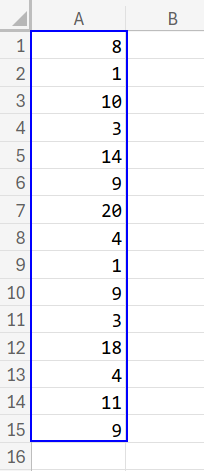
このデータには「1」も「9」も複数回登場します。
しかし、「1」の次に「9」が来ている場所は一箇所だけです。
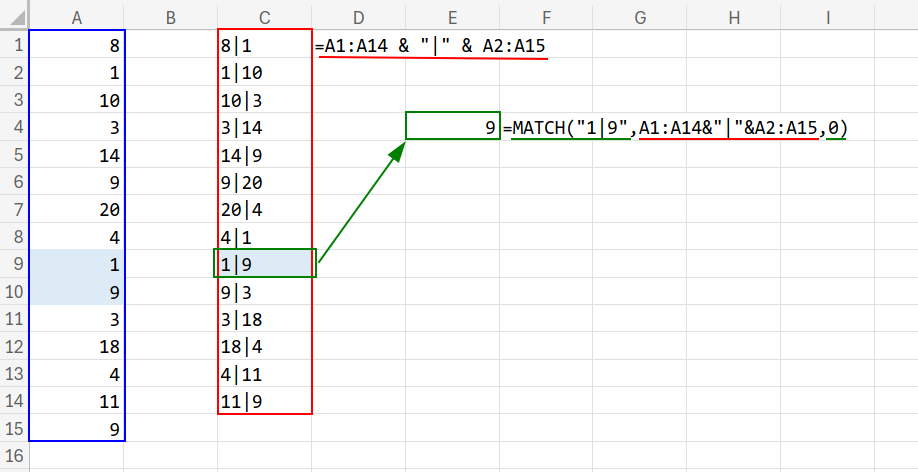
データを見ると、A9セルが「1」、A10セルが「9」になっていますね。

つまり、このパターンの先頭である「9番目」という答えを出すのが今回のゴールです。
【前提】
今回はロジックを分かりやすくするため、リスト内に「1→9」という並びは1箇所しか存在しない(重複なし)ものとして進めます。
※2次元の配列から特定のパターンを検索する方法は以下の記事で紹介しています!
初心者でも分かる!工夫とアイディアの数式
関数の詳細な仕様については、Microsoft公式のヘルプも参考にしてください。
1. 文字列でくっつけて探す(MATCH & 文字列結合)
はじめに、一番直感的で分かりやすい方法から。
「2つのセル」を検索できないなら、「くっつけて1つの文字」にしてしまえばいいのです!
数式と解説
=MATCH("1|9", A1:A14 & "|" & A2:A15, 0)
【難易度:★☆☆☆☆】【実用度:★★★★★】
【ロジックの分解】
1. A1:A14 & "|" & A2:A15
「自分」と「一つ下」のセルを、区切り文字「|」で結合します。"8|1", "1|10", "10|3" ... "1|9" ... という新しいリストが内部で作られます。
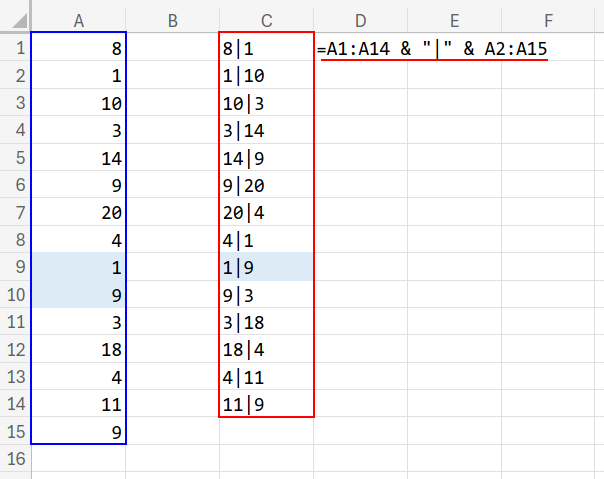
2. MATCH("1|9", ..., 0)
そのリストの中から、”1|9” という文字列を探します。
第3引数の「0」は「完全一致」という意味です。
これを忘れると正しい答えが出ないので、初心者の方は必ず「MATCHの最後は0!」と覚えておきましょう。
2. 論理値の掛け算(MATCH & 論理積)
次に、計算だけで探す方法です。「条件A かつ 条件B」を数式でどう表現するかがポイントです。
数式と解説
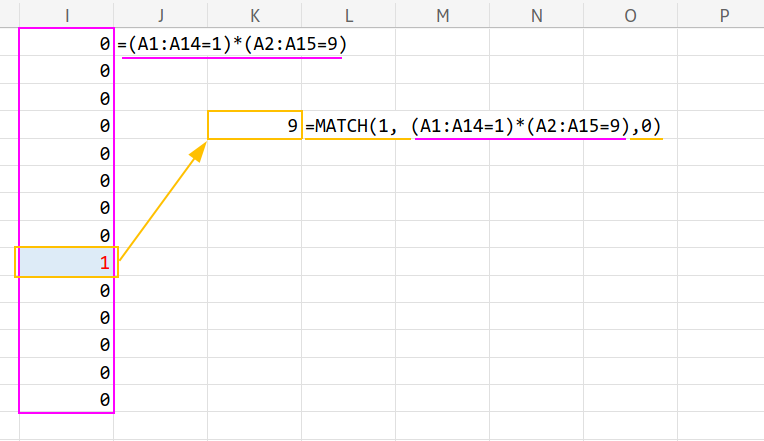
=MATCH(1, (A1:A14=1)*(A2:A15=9), 0)
【難易度:★★☆☆☆】【実用度:★★★★☆】
【ロジックの分解】
1. (A1:A14=1):自分が「1」であるか?(TRUE / FALSE)
2. (A2:A15=9):一つ下が「9」であるか?(TRUE / FALSE)
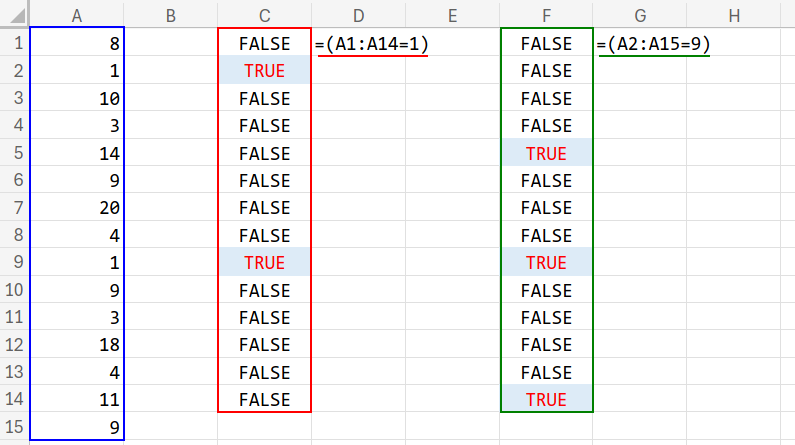
3. (...) * (...):2つの結果を掛け算します。
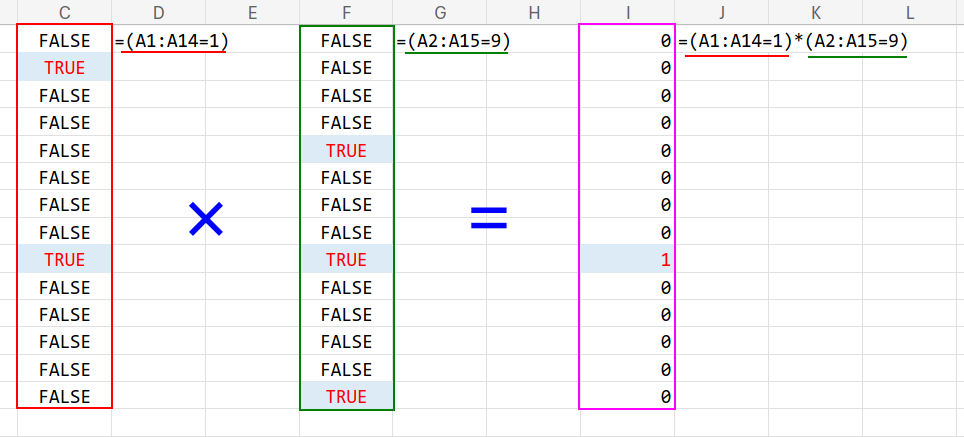
4. MATCH(1, ..., 0):掛け算の結果が「1」になった場所を探します。
3. 最新関数でスマートに(XMATCH & DROP)
続いて、Excel 2021以降やMicrosoft 365を使っているなら、範囲を手動でズラす(A1:A14とA2:A15)必要はありません。
DROP関数を使えば、範囲指定は「A1:A15」だけで済みます。
数式と解説
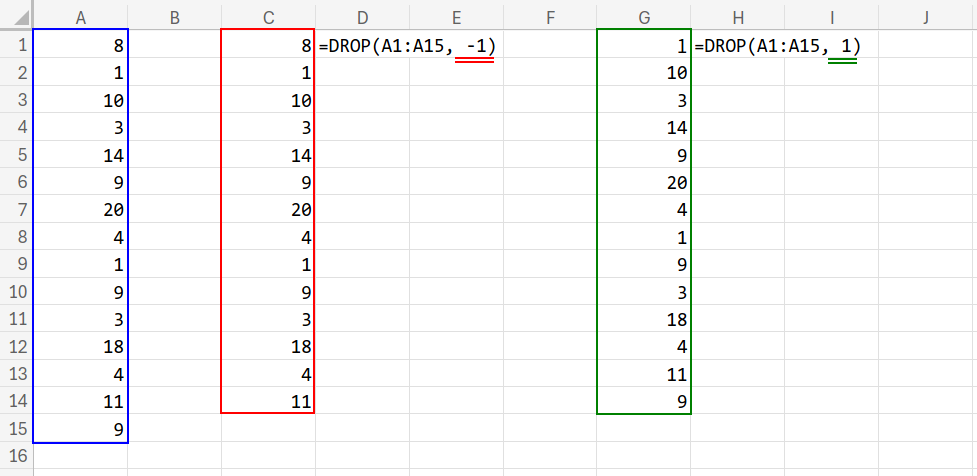
=XMATCH(1, (DROP(A1:A15,-1)=1) * (DROP(A1:A15,1)=9))
【難易度:★★★☆☆】【実用度:★★★★★】
【ロジックの分解】
1. DROP(A1:A15, -1):リストの「一番下」を削除します。(つまり A1:A14 と同じ)
2. DROP(A1:A15, 1):リストの「一番上」を削除します。(つまり A2:A15 と同じ)
あとは数式2と同じ掛け算ロジックで判定し、XMATCH(MATCHの進化版)で検索します。
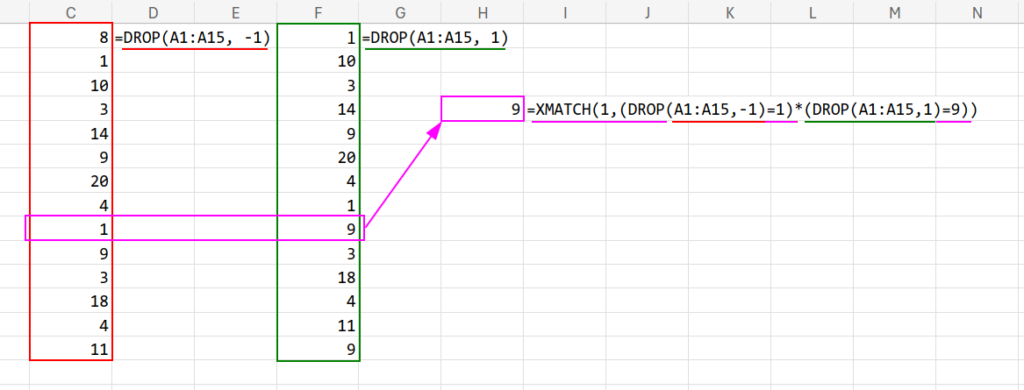
※XMATCHはデフォルトで「完全一致」なので、最後の「0」を省略できるのが嬉しいですね!
中級者へのステップアップ!配列操作テクニック
4. フィルターで該当行を抽出(FILTER & LET)
ここからは配列操作の本番です。「条件に合うものだけを抜き出す」といえば、FILTER関数の出番です。
数式と解説
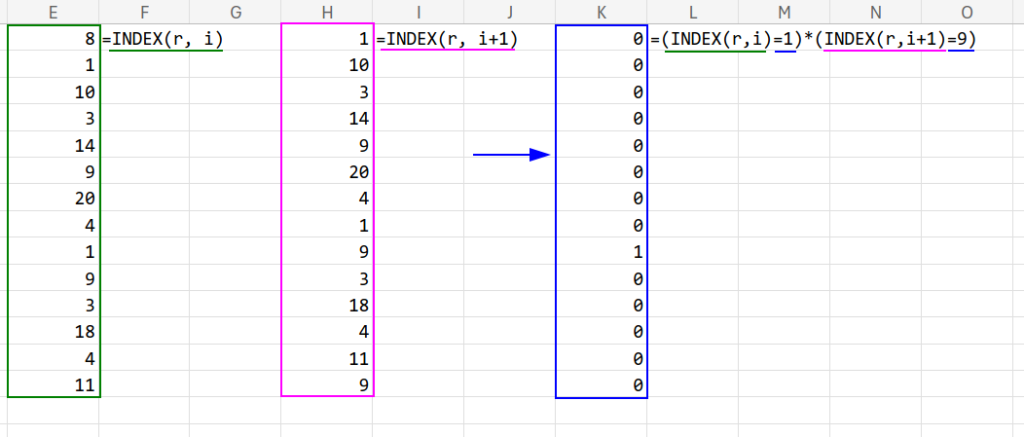
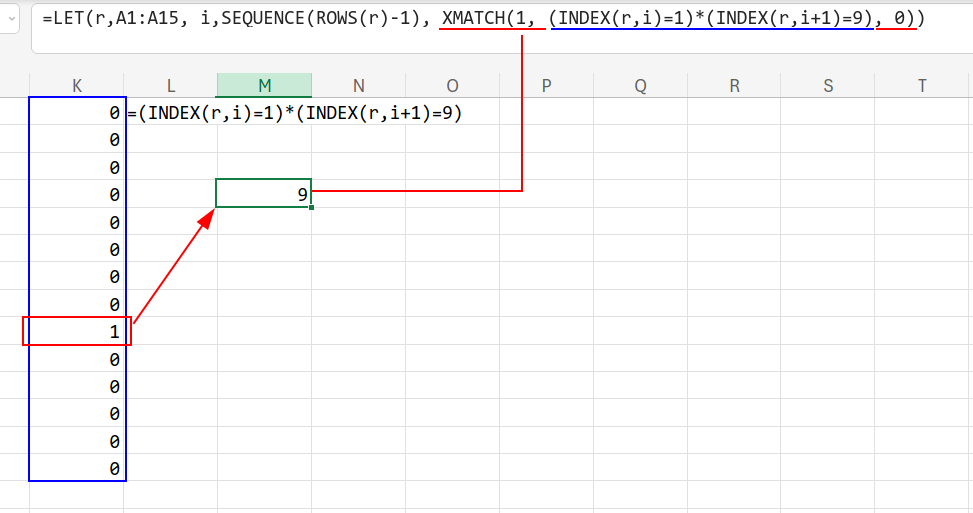
=LET(r,A1:A15, i,SEQUENCE(ROWS(r)-1), INDEX(FILTER(i, (INDEX(r,i)=1)*(INDEX(r,i+1)=9), NA()), 1))
【難易度:★★★★☆】【実用度:★★★☆☆】
【ロジックの分解】
1. LET:変数を使える関数です。範囲を r、行番号の連番を i と定義して数式を見やすくしています。
2. INDEX(r, i) と INDEX(r, i+1):現在の行と、次の行の値を比較します。
3. FILTER(i, 条件, NA()):条件(1→9の並び)に一致する行番号 i を抽出します。
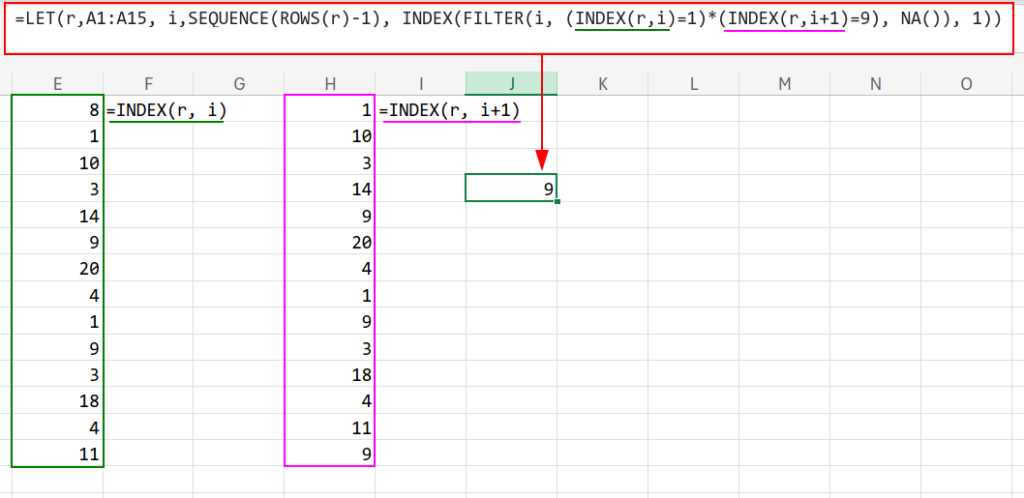
※重要ポイント:見つからなかった場合に#CALC!エラーにならないよう、第3引数に NA() を指定して「見つかりません」というエラー値を明示的に出すのが、上手なエラーハンドリング(処理)のコツです。
5. XMATCHで位置特定(XMATCH & LET)
あるいは、FILTERを使わず、直接XMATCHで探すパターンもあります。
数式と解説
=LET(r,A1:A15, i,SEQUENCE(ROWS(r)-1), XMATCH(1, (INDEX(r,i)=1)*(INDEX(r,i+1)=9), 0))
【難易度:★★★☆☆】【実用度:★★★★☆】
数式2と考え方は同じですが、LET と SEQUENCE を使うことで、参照範囲が変わっても修正が楽な「強い数式」になっています。
6. 文字列操作の極み(TEXTJOIN & FIND)
少し視点を変えて、文字列操作だけで解く方法も紹介します。
これは実務的というよりは「パズル的」な解法ですが、テキスト関数の挙動を深く理解するのに役立ちます。
数式と解説
=LET(t,","&TEXTJOIN(",",,A1:A15)&",", p,FIND(",1,9,",t), LEN(LEFT(t,p)) - LEN(SUBSTITUTE(LEFT(t,p),",","")))
【難易度:★★★★★】【アイデア度:★★★★★】
【ロジックの分解】
1.TEXTJOIN:全ての数値をカンマ区切りで連結し、",8,1,10...1,9,3..." という長い文字列を作ります。
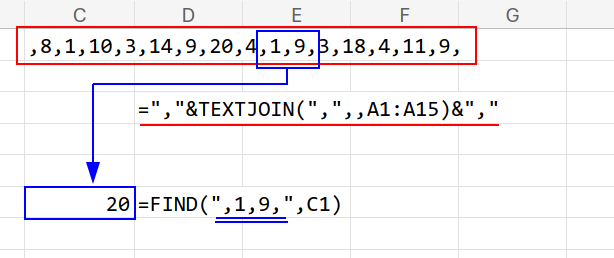
2.FIND(",1,9,", t):その中から ",1,9," という文字列が何文字目にあるかを探します。
※前後にカンマをつけるのは、「11,9」などを誤検知しないための重要な工夫です。
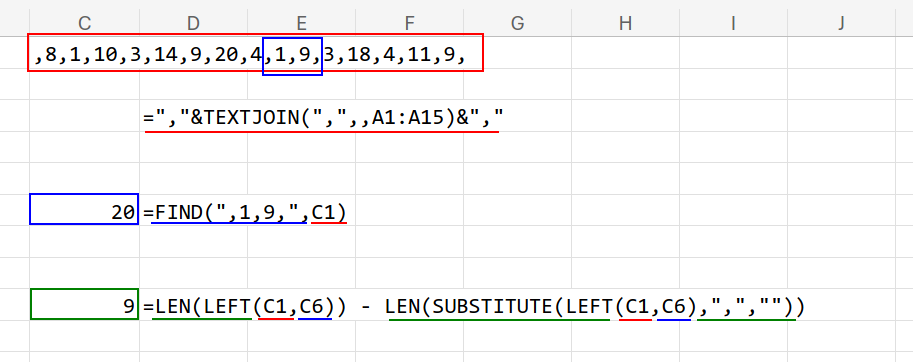
3.LEN - LEN(SUBSTITUTE(...)):見つかった場所より「左側にあるカンマの数」を数えます。
カンマの数が、そのまま「何番目のデータか」を表すことになります。
【注意】
この数式は、見つからなかった場合に #VALUE! エラーになります。実務で使うなら =IFERROR(..., NA()) などで囲むのが親切ですね。
7. 汎用性最強!MAP関数(MAP & LAMBDA)
最後に紹介するのは、Microsoft 365環境における最強の剣、MAP関数です。
数式と解説
=XMATCH(1, MAP(SEQUENCE(ROWS(A1:A15)-1), LAMBDA(i, 1*AND(INDEX(A1:A15, {0;1}+i)={1;9}))))
【難易度:★★★★★】【実用度:★★★★☆】
【この数式のすごいところ】
INDEX(..., {0;1}+i) の部分で、自分(0)と次(1)のデータを配列として取得し、{1;9} という配列と直接比較しています。
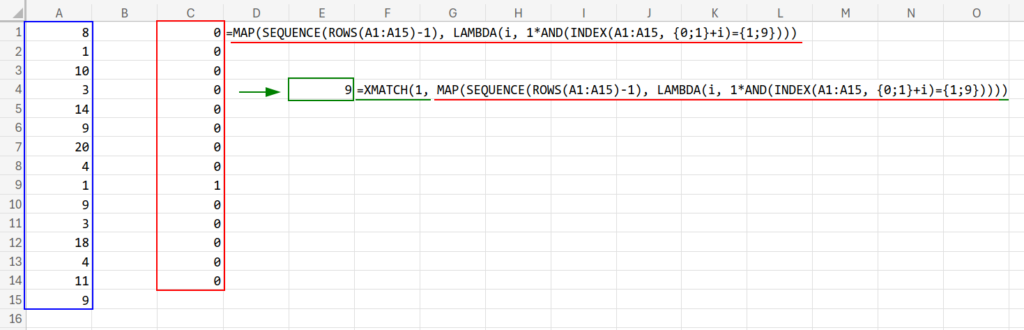
この書き方の最大のメリットは、「拡張性」です。
例えば「1→9→5→8」という4つの並びを探したくなったとしましょう。
数式1や2では修正が大変ですが、この数式なら {0;1;2;3} と {1;9;5;8} に書き換えるだけで対応できます。
複雑なパターン検索にも応用できる、プログラマライクな数式です。
まとめ:単純な検索から「パターン認識」へ
たかが2つの数字の並びですが、これを探すために
- 文字列にして探す
- 論理演算(掛け算)で探す
- 配列をズラして探す
といった多様なアプローチがありました。
これができるようになると、単なる「値の検索」だけでなく、データの「流れ」や「変化」を捉えることができるようになります。
ぜひ、あなたの手元のデータで「特定のパターン」を探してみてください。意外な発見があるかもしれませんよ!



