本記事では、無料のWeb版Excelを使用して検証および画像の作成を行っています。Windowsはもちろん、MacやLinuxの方もブラウザさえあれば挑戦できます！
はじめに：Excelで算数・数学の世界を探求しよう！
Excelの本当の面白さは、ただの表計算だけにとどまらないところにあります。
今日は、皆さんと一緒に、Excelを使って算数・数学の奥深い世界を探求する、知的な冒険に出かけたいと思います。
今回のテーマは「約数」です！
「約数…？なんだか難しそう…」
そう思ったあなた、心配はご無用です！
内容は小学生レベルの算数からスタートします。
そして、それをExcelの関数という魔法の杖を使って、目に見える形にしていく。そんな楽しい旅になりますよ。
この関数パズルを通して、あなたのExcelスキルだけでなく、数学的な思考力も自然と磨かれていくかもしれません！
さあ、準備はできましたか？数字の神秘を解き明かす冒険に出発しましょう！
ステップ1：冒険の準備 – 1から1000までの数字を用意する
何事も、まずは準備から。今回の冒険の舞台となる、1から1000までの連続した数字を用意しましょう。
まず、まっさらなシートのA1セルに「連番」と入力します。
そして、そのすぐ下のA2セルに、おなじみのこの数式を入力してください。
=SEQUENCE(1000)
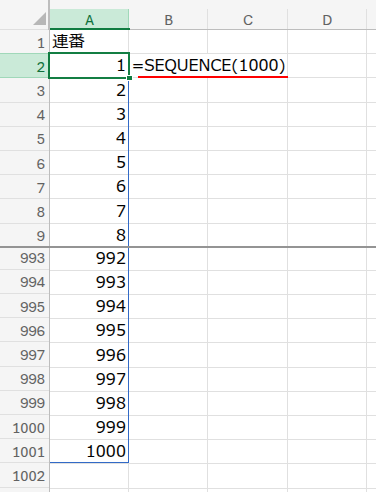
SEQUENCE関数は、指定した数の連続した数値（配列）を生成してくれる、非常に便利な関数です。
引数に「1000」と指定するだけで、あっという間に1から1000までの連番をスピル機能で表示してくれます。
どうです？これだけでもう、冒険の始まりのようでワクワクしてきませんか？
ステップ2：約数の個数を数える – 割り切れる数、いくつある？
さて、ここからが本番です！
そもそも「約数」ってなんだっけ？
「約数」とは、ある整数を割り切ることができる整数のことです。
例えば、「6」の約数を考えてみましょう。
- 6 ÷ 1 = 6 （割り切れる！）→ 1は6の約数
- 6 ÷ 2 = 3 （割り切れる！）→ 2は6の約数
- 6 ÷ 3 = 2 （割り切れる！）→ 3は6の約数
- 6 ÷ 4 = 1.5 （割り切れない…）
- 6 ÷ 5 = 1.2 （割り切れない…）
- 6 ÷ 6 = 1 （割り切れる！）→ 6は6の約数
つまり、6の約数は「1, 2, 3, 6」の4個、ということになります。簡単ですよね？
【豆知識】約数が分かると何が嬉しいの？
約数は、素因数分解（数を素数の積で表すこと）の基礎となり、暗号技術（RSA暗号など）や、物を綺麗に並べる方法（例: 12個のお菓子を2×6, 3×4, 1×12の長方形に並べる）など、実は身の回りの様々な場面で活躍している、縁の下の力持ちなのです！
Excel関数で「約数の個数」を数えよう！
この「割り切れるかどうか」というロジックを、Excel関数で表現してみましょう。
「割り切れる」ということは、言い換えれば「割った余りが0になる」ということですよね？
この考え方を素直に数式にすると、とても分かりやすくなります。
B1セルに「約数の個数」と入力し、B2セルに以下の数式を入力します。
=SUM(N(MOD(A2,SEQUENCE(A2))=0))
入力したら、B2セルのフィルハンドルをダブルクリックして、一番下まで数式をコピーしてください。
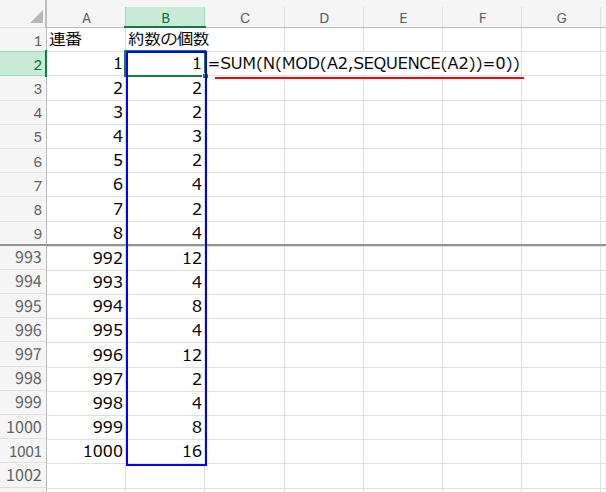
さあ、A列の数字に対応する約数の個数が一瞬で計算されました！
数式の解説
この数式、一体何をしているのでしょうか？分解してみましょう！
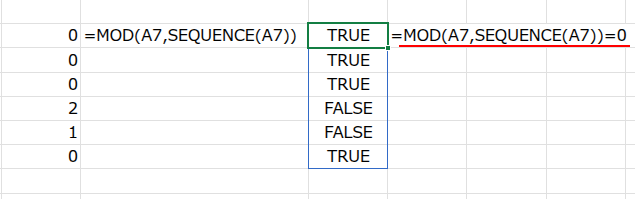
ここではA7セル「6」の場合を例にします。
・SEQUENCE(A7): まず、SEQUENCE関数が、1からA2セル（6）までの連番 {1;2;3;4;5;6} を作ります。これが「割る数」の候補になります。
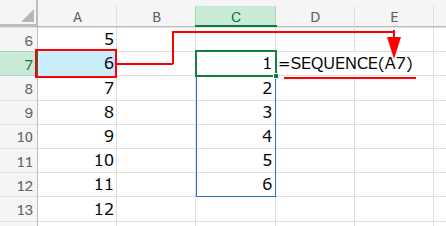
・MOD(A7,SEQUENCE(A7)): 次に、MOD関数が、A7セル（6）を、先ほど作った連番で一つずつ割った「余り」を計算していきます。結果は {0;0;0;2;1;0} という、余りの配列になります。
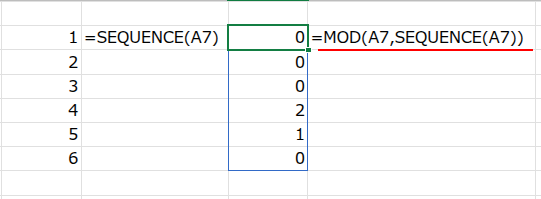
・... = 0: この余りの配列が、「0」と等しいかどうかを判定します。余りが0（つまり割り切れた）の部分はTRUE、そうでない部分はFALSEになります。
結果は {TRUE;TRUE;TRUE;FALSE;FALSE;TRUE} という論理値の配列です。
・N(...): N関数が、このTRUE/FALSEの配列を、数値の1/0に変換します。{1;1;1;0;0;1}
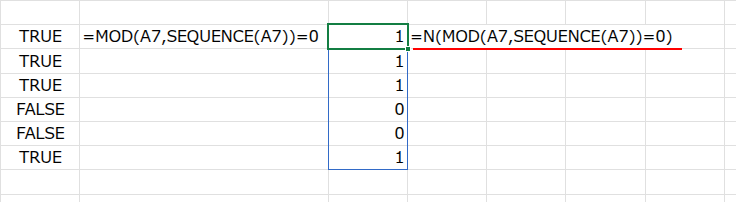
・SUM(...): 最後に、SUM関数がこの1と0の配列を合計します。
1の個数、つまり割り切れた数＝約数の個数が「4」と計算されるわけです。直感的で分かりやすいですよね！
もう一つの考え方
ちなみに、割り算の結果そのものを使って判定する方法もあります。
=SUM(N(A2/SEQUENCE(A2)=INT(A2/SEQUENCE(A2))))
という数式です。
これは、「割り算の結果」と「割り算の結果の整数部分」が等しいかどうかを比較しています。
割り切れたときだけ両者が一致することを利用した、こちらも非常に賢いロジックですね！
ステップ3：素数を見つけ出す – 約数が2個だけの特別な数
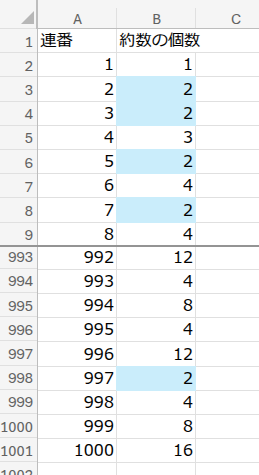
さて、B列に並んだ「約数の個数」をじっと眺めてみてください。
何か気づくことはありませんか？
そう、「2」という数字が頻繁に登場しますよね。この「約数の個数が2個」である数こそが、数学の世界で非常に重要な「素数」なのです！
「素数」とは？
素数とは、「1とその数自身しか約数を持たない、1より大きい自然数」のことです。
例えば、「5」の約数は「1, 5」の2個だけ。だから5は素数です。
「7」の約数も「1, 7」の2個だけ。だから7も素数です。
でも、「6」の約数は「1, 2, 3, 6」の4個なので、素数ではありません。
この素数、実は現代のインターネットを支える暗号技術の根幹をなす、とてつもなく重要な数なのです。
ロマンがありますよね！
素数を求める数式は、実は様々なアプローチがあり、以下の記事でも紹介していますよ！
LET関数で、素数を華麗に抽出しよう！
では、B列の結果を使って、1から1000までに含まれる素数だけをリストアップしてみましょう。
これまでの記事では、数式を分かりやすくするために「名前の定義」を使ってきました。
今回は、それと似たようなことができる最新関数、LET関数を使ってみましょう！
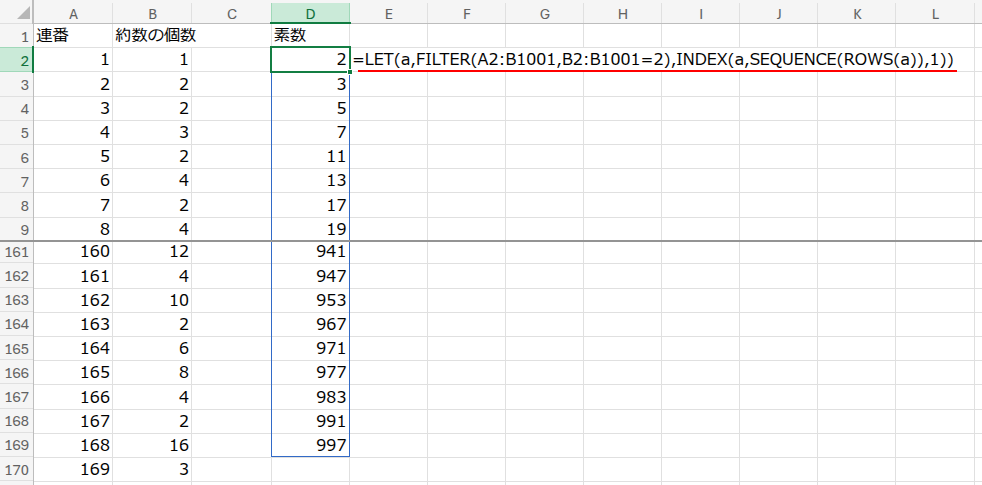
D1セルに「素数」と入力し、D2セルに以下の数式を入力します。
=LET(a,FILTER(A2:B1001,B2:B1001=2),INDEX(a,SEQUENCE(ROWS(a)),1))
どうでしょう？スピル機能で、1から1000までの素数が一瞬で表示されました！
この数式で使っているLET関数、初めて見る方も多いかもしれませんね。
LET関数の使い方
LET関数は、数式の中で使う計算結果や値に「名前」をつけることができる関数です。
=LET(名前1, 値1, 計算式) のように使います。
例えば、=LET(x, 10, x*5) と書くと、まず「x」という名前に「10」を記憶させ、その「x」を使って「x*5」という計算をします。
結果は「50」になります。
同じ計算を何度も繰り返す複雑な数式を、スッキリと読みやすくしてくれる、非常に強力な関数なのです！
数式の解説
このLET関数の使い方を踏まえて、数式を分解してみましょう。
・LET(a, FILTER(A2:B1001, B2:B1001=2), ...): まず、FILTER(A2:B1001, B2:B1001=2) の部分で、A列とB列のペアの中から、B列（約数の個数）が「2」であるものだけを絞り込みます。
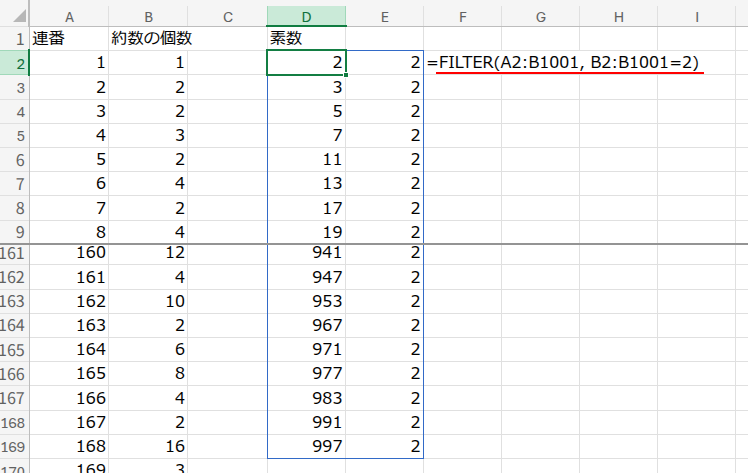
この絞り込んだ結果（素数の連番と、2という約数の個数の2列の表）に、「a」という名前をつけています。
・INDEX(a, SEQUENCE(ROWS(a)), 1): 次に、名前をつけた「a」を使って計算します。
ROWS(a)で絞り込んだ行数を取得し、SEQUENCEでその行数分の連番を生成します。
そして、INDEX関数が、「a」の表から、すべての行（SEQUENCE(...)の部分）の、1列目（素数の連番）だけを取り出しているのです。
面白い別解：約数が3つの数から素数を探す
ここで、少し頭の体操です。こんな方法でも素数を見つけることができます。
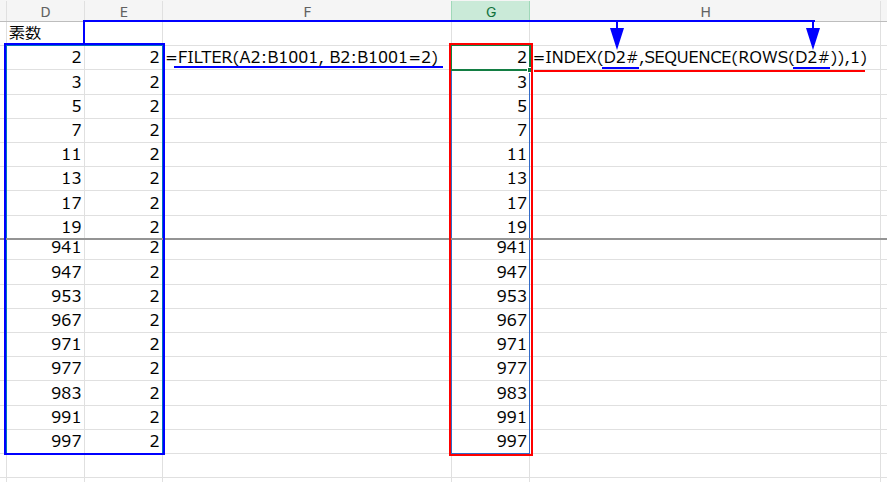
=LET(a,FILTER(A2:B1001,B2:B1001=3),INDEX(SQRT(a),SEQUENCE(ROWS(a)),1))
今度は、約数の個数が「3」のものを探していますね。そして、最後にSQRT関数（平方根を求める関数）を使っています。
実は、「約数が3個である数」は、必ず「素数の2乗」になるという面白い性質があるのです！
例えば、9（=3²）の約数は「1, 3, 9」の3個。25（=5²）の約数は「1, 5, 25」の3個です。
つまり、約数が3個の数を見つけ出し、その平方根を取れば、それもまた素数になる、というわけです。数学って面白いですよね！
ステップ4：最も約数の多い数 – 1000までのナンバーワンは誰だ？
さて、ここで素朴な疑問です。
1から1000までの数字の中で、一体どの数字が最も多くの約数を持っているのでしょうか？
これもExcelなら一瞬で答えがわかります。SORT関数で並べ替えてみましょう！
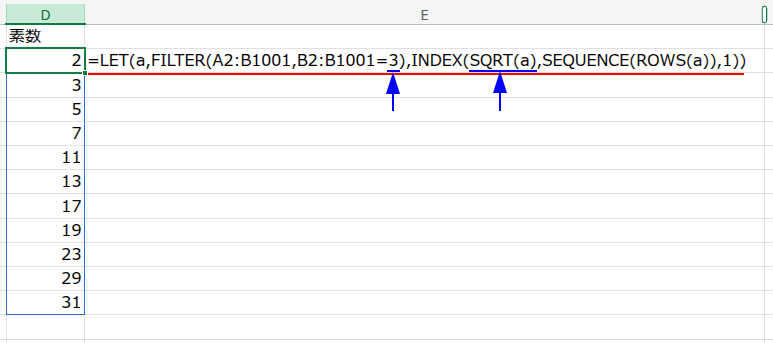
G1セルに「並べ替え」と入力し、G2セルに以下の数式を入力します。
=SORT(A2:B1001,2,-1)
SORT関数は、指定した範囲を並べ替える関数です。
- 第1引数 A2:B1001: 並べ替えたい範囲
- 第2引数 2: 何列目を基準に並べ替えるか（今回は2列目の「約数の個数」）
- 第3引数 -1: どのように並べ替えるか（-1は降順、つまり大きい順）
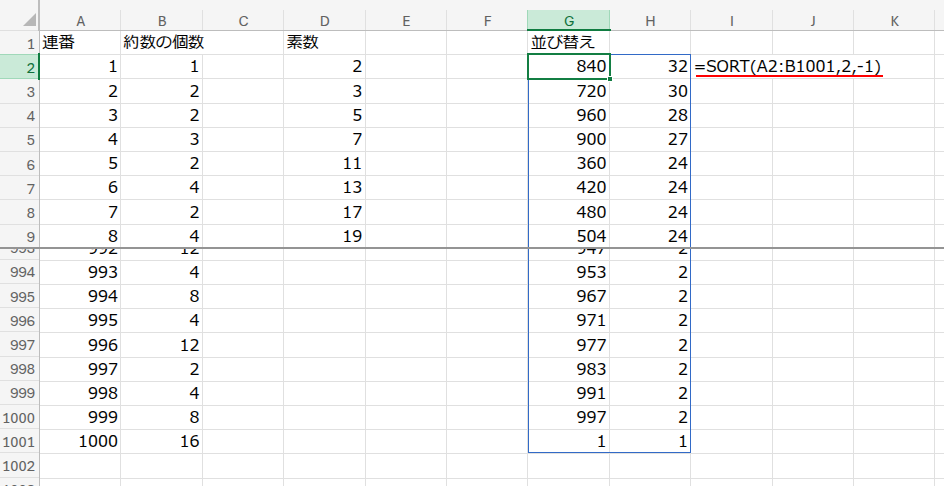
結果は…なんと「840」が32個の約数を持ち、堂々の1位でした！
なぜ840はこんなに約数が多いのでしょうか？
それは、840が「2, 3, 5, 7」といった、小さい素数をたくさん因数に持っている（840 = 2³ × 3 × 5 × 7）ためです。
このような数を「高度合成数」と呼び、非常に割り切りやすい、キリのいい数として重宝されます。
例えば、1日は86400秒ですが、これも高度合成数で、様々な時間単位（60秒, 60分など）で割り切りやすくなっています。面白い発見ですよね！
ステップ5：約数の一覧を表示する – どんな数で割り切れる？
最後に、指定した数字の約数を、すべてリストアップする数式に挑戦しましょう。
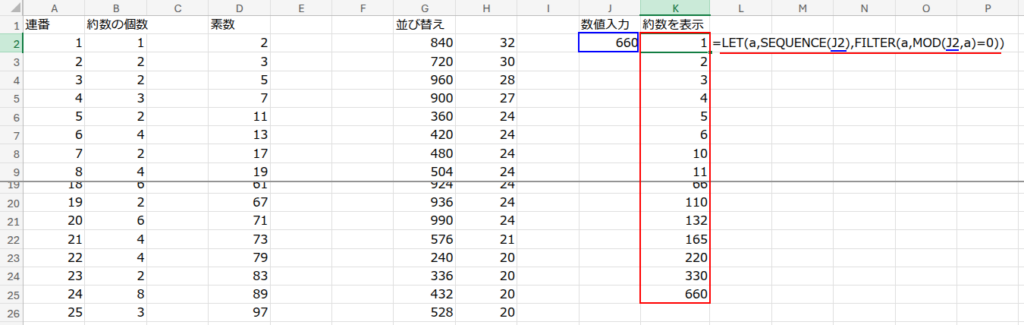
J1セルに「数値入力」と入力し、J2セルに好きな数字を入れてみてください。ここでは「660」にしてみましょう。
K1セルに「約数を表示」と入力し、K2セルに以下の数式を入力します。
=LET(a,SEQUENCE(J2),FILTER(a,MOD(J2,a)=0))
どうでしょう？
J2セルに入力した「660」の約数が、ズラッと表示されました！
この数式も、LET関数を使っていて、とてもシンプルです。
・LET(a, SEQUENCE(J2), ...): まず、SEQUENCE関数で1からJ2セル（660）までの連番を作り、それに「a」という名前をつけています。
・FILTER(a, MOD(J2,a)=0): 次に、FILTER関数が、名前をつけた「a」（1から660までの連番）の中から、条件に合うものだけを絞り込んでいます。
その条件とは、MOD(J2,a)=0、つまり「660をaで割った余りが0になる」もの。これぞまさしく「約数」の定義そのものですね！
J2セルの値を「840」や、ご自身の好きな数字に変えて、結果がどう変わるか試してみてください！
まとめ：Excelは、数学の最高の遊び場だ！
「約数」という一つのテーマから、「素数」の発見、そして「最も約数の多い数」の探求まで、Excelがいかに数学的な思考の遊び場として優れているか、感じていただけたのではないでしょうか。
難しいと思っていた数式も、分解してみれば、その一つひとつは「割り切れるかな？」「余りはいくつかな？」といった、シンプルな算数の組み合わせでできています。
今回の関数パズルが、皆さんのExcelへの興味をさらに深め、数字の世界の面白さを再発見するきっかけになれば、これほど嬉しいことはありません。
